Gaussian kernel expansion with basis functions uniformly bounded in $\mathcal{L}_{\infty}$

Kernel expansions are a topic of considerable interest in machine learning, also because of their relation to the so-called feature maps introduced in machine learning. Properties of the associated basis functions and weights (corresponding to eigenfunctions and eigenvalues in the Mercer setting) give insight into for example the structure of the associated reproducing kernel Hilbert space, the goodness of approximation schemes, the convergence rates and generalization properties of kernel machines. Recent work in the literature has derived some of these results by assuming uniformly bounded basis functions in $\mathcal{L}_\infty$. Motivated by this line of research, we investigate under this constraint all possible kernel expansions of the Gaussian kernel, one of the most widely used models in machine learning. Our main result is the construction on $\mathbb{R}^2$ of a Gaussian kernel expansion with weights in $\ell_p$ for any $p>1$. This result is optimal since we also prove that $p=1$ cannot be reached by the Gaussian kernel, nor by any of the other radial basis function kernels commonly used in the literature. A consequence for this kind of kernels is also the non-existence of Mercer expansions on $\mathbb{R}^2$, with respect to any finite measure, whose eigenfunctions all belong to a closed ball of $\mathcal{L}_\infty$.

Kernel-based function learning in dynamic and non stationary environments

One central theme in machine learning is function estimation from sparse and noisy data. An example is supervised learning where the elements of the training set are couples, each containing an input location and an output response. In the last decades, a substantial amount of work has been devoted to design estimators for the unknown function and to study their convergence to the optimal predictor, also characterizing the learning rate. These results typically rely on stationary assumptions where input locations are drawn from a probability distribution that does not change in time. In this work, we consider kernel-based ridge regression and derive convergence conditions under non stationary distributions, addressing also cases where stochastic adaption may happen infinitely often. This includes the important exploration-exploitation problems where e.g. a set of agents/robots has to monitor an environment to reconstruct a sensorial field and their movements rules are continuously updated on the basis of the acquired knowledge on the field and/or the surrounding environment.

Absolute integrability of Mercer kernels is only sufficient for RKHS stability

Reproducing kernel Hilbert spaces (RKHSs) are special Hilbert spaces in one-to-one correspondence with positive definite maps called kernels. They are widely employed in machine learning to reconstruct unknown functions from sparse and noisy data. In the last two decades, a subclass known as stable RKHSs has been also introduced in the setting of linear system identification. Stable RKHSs contain only absolutely integrable impulse responses over the positive real line. Hence, they can be adopted as hypothesis spaces to estimate linear, time-invariant and BIBO stable dynamic systems from input-output data. Necessary and sufficient conditions for RKHS stability are available in the literature and it is known that kernel absolute integrability implies stability. Working in discrete-time, in a recent work we have proved that this latter condition is only sufficient. Working in continuous-time, it is the purpose of this note to prove that the same result holds also for Mercer kernels.

On the stability test for reproducing kernel Hilbert spaces

Reproducing kernel Hilbert spaces (RKHSs) are special Hilbert spaces where all the evaluation functionals are linear and bounded. They are in one-to-one correspondence with positive definite maps called kernels. Stable RKHSs enjoy the additional property of containing only functions and absolutely integrable. Necessary and sufficient conditions for RKHS stability are known in the literature: the integral operator induced by the kernel must be bounded as map between $\mathcal{L}_{\infty}$, the space of essentially bounded (test) functions, and $\mathcal{L}_1$, the space of absolutely integrable functions. Considering Mercer (continuous) kernels in continuous-time and the entire discrete-time class, we show that the stability test can be reduced to the study of the kernel operator over test functions which assume (almost everywhere) only the values $\pm 1$. They represent the same functions needed to investigate stability of any single element in the RKHS. In this way, the RKHS stability test becomes an elegant generalization of a straightforward result concerning Bounded-Input Bounded-Output (BIBO) stability of a single linear time-invariant system.

Dealing with Collinearity in Large-Scale Linear System Identification Using Gaussian Regression

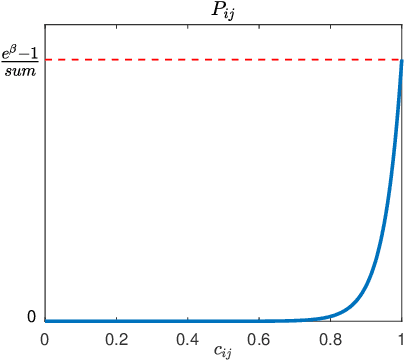
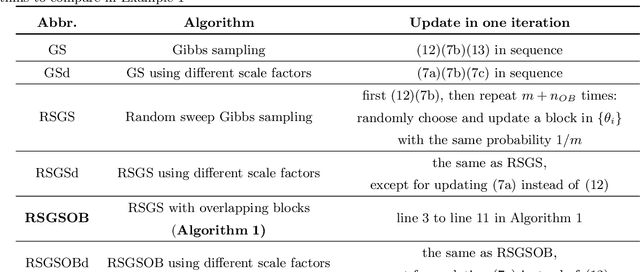
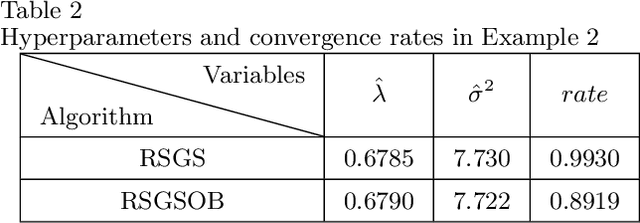
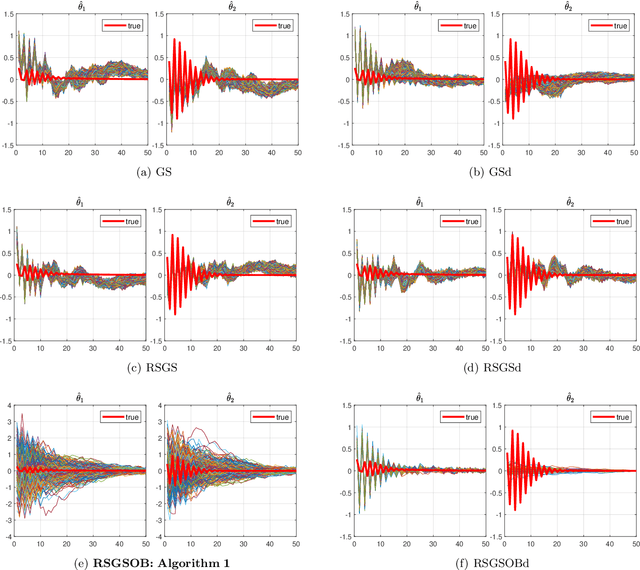
Many problems arising in control require the determination of a mathematical model of the application. This has often to be performed starting from input-output data, leading to a task known as system identification in the engineering literature. One emerging topic in this field is estimation of networks consisting of several interconnected dynamic systems. We consider the linear setting assuming that system outputs are the result of many correlated inputs, hence making system identification severely ill-conditioned. This is a scenario often encountered when modeling complex cybernetics systems composed by many sub-units with feedback and algebraic loops. We develop a strategy cast in a Bayesian regularization framework where any impulse response is seen as realization of a zero-mean Gaussian process. Any covariance is defined by the so called stable spline kernel which includes information on smooth exponential decay. We design a novel Markov chain Monte Carlo scheme able to reconstruct the impulse responses posterior by efficiently dealing with collinearity. Our scheme relies on a variation of the Gibbs sampling technique: beyond considering blocks forming a partition of the parameter space, some other (overlapping) blocks are also updated on the basis of the level of collinearity of the system inputs. Theoretical properties of the algorithm are studied obtaining its convergence rate. Numerical experiments are included using systems containing hundreds of impulse responses and highly correlated inputs.

Deep networks for system identification: a Survey

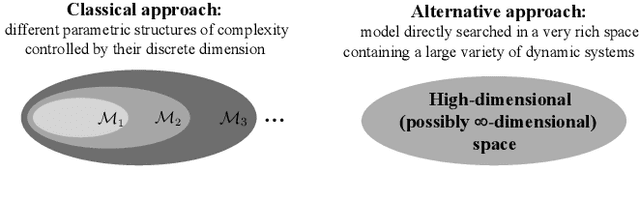
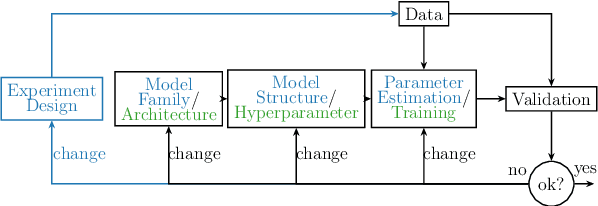
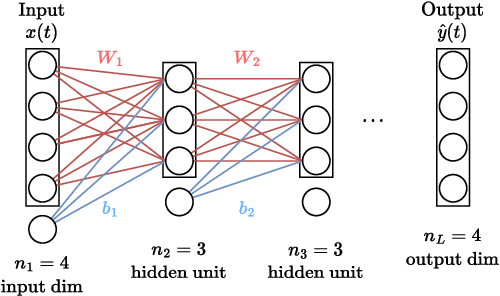
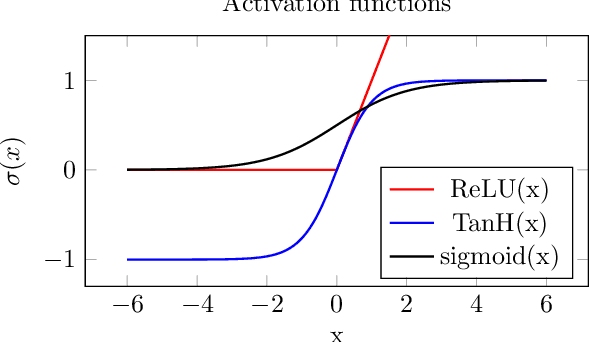
Deep learning is a topic of considerable current interest. The availability of massive data collections and powerful software resources has led to an impressive amount of results in many application areas that reveal essential but hidden properties of the observations. System identification learns mathematical descriptions of dynamic systems from input-output data and can thus benefit from the advances of deep neural networks to enrich the possible range of models to choose from. For this reason, we provide a survey of deep learning from a system identification perspective. We cover a wide spectrum of topics to enable researchers to understand the methods, providing rigorous practical and theoretical insights into the benefits and challenges of using them. The main aim of the identified model is to predict new data from previous observations. This can be achieved with different deep learning based modelling techniques and we discuss architectures commonly adopted in the literature, like feedforward, convolutional, and recurrent networks. Their parameters have to be estimated from past data trying to optimize the prediction performance. For this purpose, we discuss a specific set of first-order optimization tools that is emerged as efficient. The survey then draws connections to the well-studied area of kernel-based methods. They control the data fit by regularization terms that penalize models not in line with prior assumptions. We illustrate how to cast them in deep architectures to obtain deep kernel-based methods. The success of deep learning also resulted in surprising empirical observations, like the counter-intuitive behaviour of models with many parameters. We discuss the role of overparameterized models, including their connection to kernels, as well as implicit regularization mechanisms which affect generalization, specifically the interesting phenomena of benign overfitting ...

Dealing with collinearity in large-scale linear system identification using Bayesian regularization

We consider the identification of large-scale linear and stable dynamic systems whose outputs may be the result of many correlated inputs. Hence, severe ill-conditioning may affect the estimation problem. This is a scenario often arising when modeling complex physical systems given by the interconnection of many sub-units where feedback and algebraic loops can be encountered. We develop a strategy based on Bayesian regularization where any impulse response is modeled as the realization of a zero-mean Gaussian process. The stable spline covariance is used to include information on smooth exponential decay of the impulse responses. We then design a new Markov chain Monte Carlo scheme that deals with collinearity and is able to efficiently reconstruct the posterior of the impulse responses. It is based on a variation of Gibbs sampling which updates possibly overlapping blocks of the parameter space on the basis of the level of collinearity affecting the different inputs. Numerical experiments are included to test the goodness of the approach where hundreds of impulse responses form the system and inputs correlation may be very high.

Mathematical foundations of stable RKHSs

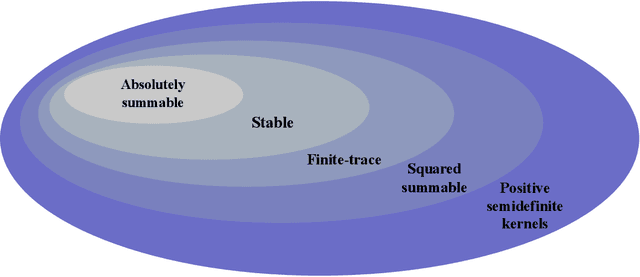
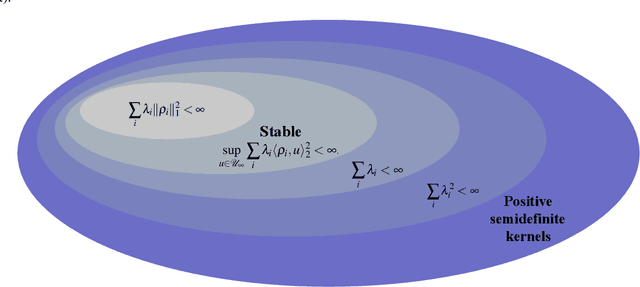
Reproducing kernel Hilbert spaces (RKHSs) are key spaces for machine learning that are becoming popular also for linear system identification. In particular, the so-called stable RKHSs can be used to model absolutely summable impulse responses. In combination e.g. with regularized least squares they can then be used to reconstruct dynamic systems from input-output data. In this paper we provide new structural properties of stable RKHSs. The relation between stable kernels and other fundamental classes, like those containing absolutely summable or finite-trace kernels, is elucidated. These insights are then brought into the feature space context. First, it is proved that any stable kernel admits feature maps induced by a basis of orthogonal eigenvectors in l2. The exact connection with classical system identification approaches that exploit such kind of functions to model impulse responses is also provided. Then, the necessary and sufficient stability condition for RKHSs designed by formulating kernel eigenvectors and eigenvalues is obtained. Overall, our new results provide novel mathematical foundations of stable RKHSs with impact on stability tests, impulse responses modeling and computational efficiency of regularized schemes for linear system identification.

Kernel absolute summability is only sufficient for RKHS stability

Regularized approaches have been successfully applied to linear system identification in recent years. Many of them model unknown impulse responses exploiting the so called Reproducing Kernel Hilbert spaces (RKHSs) that enjoy the notable property of being in one-to-one correspondence with the class of positive semidefinite kernels. The necessary and sufficient condition for a RKHS to be stable, i.e. to contain only BIBO stable linear dynamic systems, has been known in the literature at least since 2006. However, an open question still persists and concerns the equivalence of such condition with the absolute summability of the kernel. This paper provides a definite answer to this matter by proving that such correspondence does not hold. A counterexample is introduced that illustrates the existence of stable RKHSs that are induced by non-absolutely summable kernels.

A novel Multiplicative Polynomial Kernel for Volterra series identification

Volterra series are especially useful for nonlinear system identification, also thanks to their capability to approximate a broad range of input-output maps. However, their identification from a finite set of data is hard, due to the curse of dimensionality. Recent approaches have shown how regularized kernel-based methods can be useful for this task. In this paper, we propose a new regularization network for Volterra models identification. It relies on a new kernel given by the product of basic building blocks. Each block contains some unknown parameters that can be estimated from data using marginal likelihood optimization. In comparison with other algorithms proposed in the literature, numerical experiments show that our approach allows to better select the monomials that really influence the system output, much increasing the prediction capability of the model.