Real2Sim based on Active Perception with automatically VLM-generated Behavior Trees

Constructing an accurate simulation model of real-world environments requires reliable estimation of physical parameters such as mass, geometry, friction, and contact surfaces. Traditional real-to-simulation (Real2Sim) pipelines rely on manual measurements or fixed, pre-programmed exploration routines, which limit their adaptability to varying tasks and user intents. This paper presents a Real2Sim framework that autonomously generates and executes Behavior Trees for task-specific physical interactions to acquire only the parameters required for a given simulation objective, without relying on pre-defined task templates or expert-designed exploration routines. Given a high-level user request, an incomplete simulation description, and an RGB observation of the scene, a vision-language model performs multi-modal reasoning to identify relevant objects, infer required physical parameters, and generate a structured Behavior Tree composed of elementary robotic actions. The resulting behavior is executed on a torque-controlled Franka Emika Panda, enabling compliant, contact-rich interactions for parameter estimation. The acquired measurements are used to automatically construct a physics-aware simulation. Experimental results on the real manipulator demonstrate estimation of object mass, surface height, and friction-related quantities across multiple scenarios, including occluded objects and incomplete prior models. The proposed approach enables interpretable, intent-driven, and autonomously Real2Sim pipelines, bridging high-level reasoning with physically-grounded robotic interaction.

Learning global control of underactuated systems with Model-Based Reinforcement Learning

This short paper describes our proposed solution for the third edition of the "AI Olympics with RealAIGym" competition, held at ICRA 2025. We employed Monte-Carlo Probabilistic Inference for Learning Control (MC-PILCO), an MBRL algorithm recognized for its exceptional data efficiency across various low-dimensional robotic tasks, including cart-pole, ball \& plate, and Furuta pendulum systems. MC-PILCO optimizes a system dynamics model using interaction data, enabling policy refinement through simulation rather than direct system data optimization. This approach has proven highly effective in physical systems, offering greater data efficiency than Model-Free (MF) alternatives. Notably, MC-PILCO has previously won the first two editions of this competition, demonstrating its robustness in both simulated and real-world environments. Besides briefly reviewing the algorithm, we discuss the most critical aspects of the MC-PILCO implementation in the tasks at hand: learning a global policy for the pendubot and acrobot systems.

Data-driven Power Loss Identification through Physics-Based Thermal Model Backpropagation

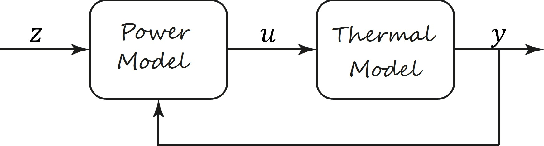
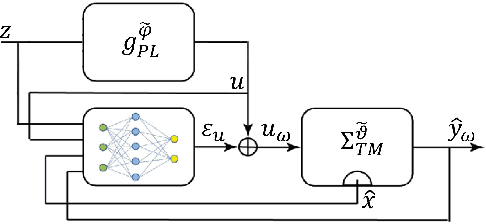
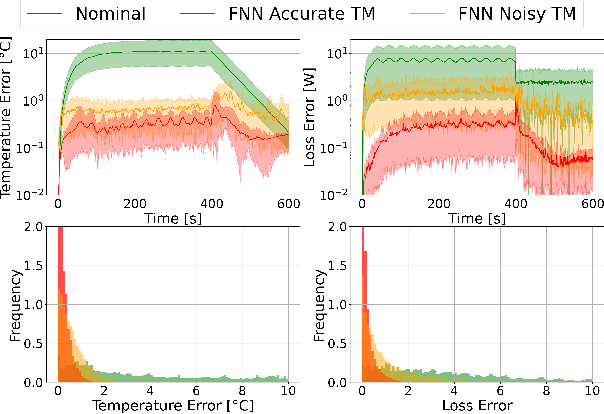
Digital twins for power electronics require accurate power losses whose direct measurements are often impractical or impossible in real-world applications. This paper presents a novel hybrid framework that combines physics-based thermal modeling with data-driven techniques to identify and correct power losses accurately using only temperature measurements. Our approach leverages a cascaded architecture where a neural network learns to correct the outputs of a nominal power loss model by backpropagating through a reduced-order thermal model. We explore two neural architectures, a bootstrapped feedforward network, and a recurrent neural network, demonstrating that the bootstrapped feedforward approach achieves superior performance while maintaining computational efficiency for real-time applications. Between the interconnection, we included normalization strategies and physics-guided training loss functions to preserve stability and ensure physical consistency. Experimental results show that our hybrid model reduces both temperature estimation errors (from 7.2+-6.8{\deg}C to 0.3+-0.3{\deg}C) and power loss prediction errors (from 5.4+-6.6W to 0.2+-0.3W) compared to traditional physics-based approaches, even in the presence of thermal model uncertainties. This methodology allows us to accurately estimate power losses without direct measurements, making it particularly helpful for real-time industrial applications where sensor placement is hindered by cost and physical limitations.

Towards Autonomous Reinforcement Learning for Real-World Robotic Manipulation with Large Language Models

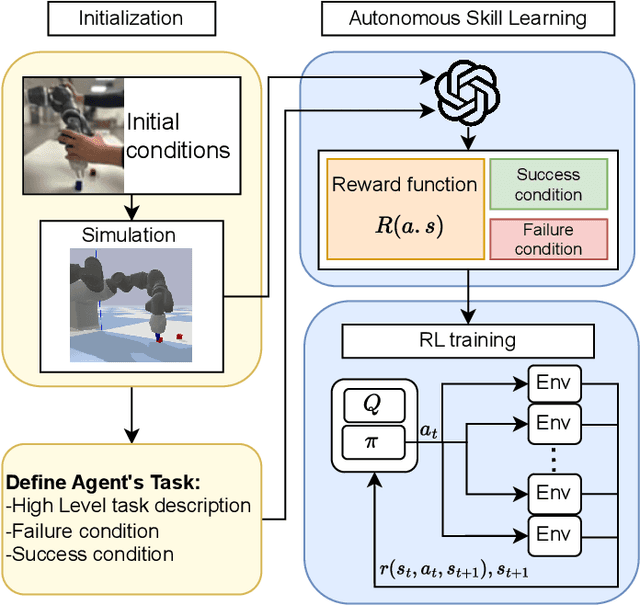
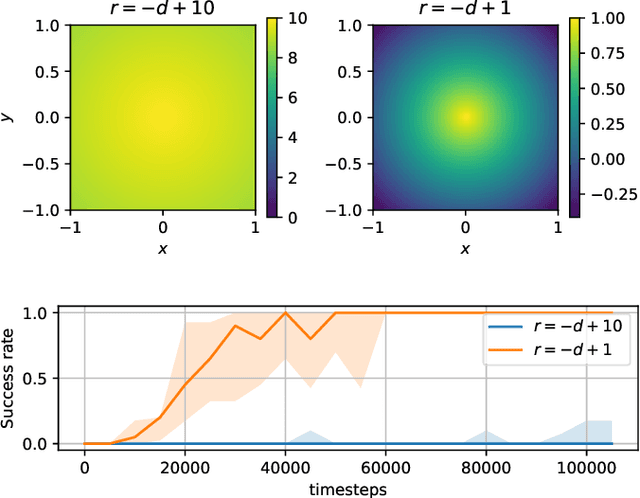
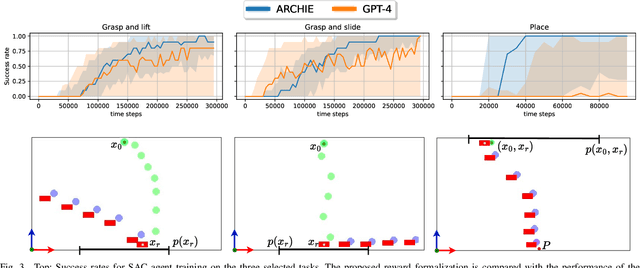
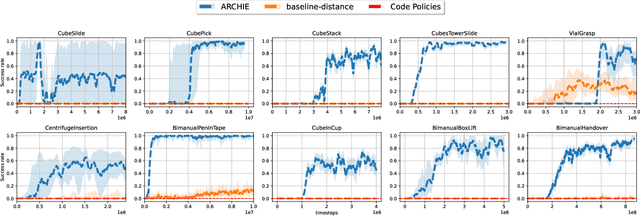
Recent advancements in Large Language Models (LLMs) and Visual Language Models (VLMs) have significantly impacted robotics, enabling high-level semantic motion planning applications. Reinforcement Learning (RL), a complementary paradigm, enables agents to autonomously optimize complex behaviors through interaction and reward signals. However, designing effective reward functions for RL remains challenging, especially in real-world tasks where sparse rewards are insufficient and dense rewards require elaborate design. In this work, we propose Autonomous Reinforcement learning for Complex HumanInformed Environments (ARCHIE), an unsupervised pipeline leveraging GPT-4, a pre-trained LLM, to generate reward functions directly from natural language task descriptions. The rewards are used to train RL agents in simulated environments, where we formalize the reward generation process to enhance feasibility. Additionally, GPT-4 automates the coding of task success criteria, creating a fully automated, one-shot procedure for translating human-readable text into deployable robot skills. Our approach is validated through extensive simulated experiments on single-arm and bi-manual manipulation tasks using an ABB YuMi collaborative robot, highlighting its practicality and effectiveness. Tasks are demonstrated on the real robot setup.

Data efficient Robotic Object Throwing with Model-Based Reinforcement Learning

Pick-and-place (PnP) operations, featuring object grasping and trajectory planning, are fundamental in industrial robotics applications. Despite many advancements in the field, PnP is limited by workspace constraints, reducing flexibility. Pick-and-throw (PnT) is a promising alternative where the robot throws objects to target locations, leveraging extrinsic resources like gravity to improve efficiency and expand the workspace. However, PnT execution is complex, requiring precise coordination of high-speed movements and object dynamics. Solutions to the PnT problem are categorized into analytical and learning-based approaches. Analytical methods focus on system modeling and trajectory generation but are time-consuming and offer limited generalization. Learning-based solutions, in particular Model-Free Reinforcement Learning (MFRL), offer automation and adaptability but require extensive interaction time. This paper introduces a Model-Based Reinforcement Learning (MBRL) framework, MC-PILOT, which combines data-driven modeling with policy optimization for efficient and accurate PnT tasks. MC-PILOT accounts for model uncertainties and release errors, demonstrating superior performance in simulations and real-world tests with a Franka Emika Panda manipulator. The proposed approach generalizes rapidly to new targets, offering advantages over analytical and Model-Free methods.

Continual Learning for Behavior-based Driver Identification

Behavior-based Driver Identification is an emerging technology that recognizes drivers based on their unique driving behaviors, offering important applications such as vehicle theft prevention and personalized driving experiences. However, most studies fail to account for the real-world challenges of deploying Deep Learning models within vehicles. These challenges include operating under limited computational resources, adapting to new drivers, and changes in driving behavior over time. The objective of this study is to evaluate if Continual Learning (CL) is well-suited to address these challenges, as it enables models to retain previously learned knowledge while continually adapting with minimal computational overhead and resource requirements. We tested several CL techniques across three scenarios of increasing complexity based on the well-known OCSLab dataset. This work provides an important step forward in scalable driver identification solutions, demonstrating that CL approaches, such as DER, can obtain strong performance, with only an 11% reduction in accuracy compared to the static scenario. Furthermore, to enhance the performance, we propose two new methods, SmooER and SmooDER, that leverage the temporal continuity of driver identity over time to enhance classification accuracy. Our novel method, SmooDER, achieves optimal results with only a 2% reduction compared to the 11\% of the DER approach. In conclusion, this study proves the feasibility of CL approaches to address the challenges of Driver Identification in dynamic environments, making them suitable for deployment on cloud infrastructure or directly within vehicles.

Edge Delayed Deep Deterministic Policy Gradient: efficient continuous control for edge scenarios

Deep Reinforcement Learning is gaining increasing attention thanks to its capability to learn complex policies in high-dimensional settings. Recent advancements utilize a dual-network architecture to learn optimal policies through the Q-learning algorithm. However, this approach has notable drawbacks, such as an overestimation bias that can disrupt the learning process and degrade the performance of the resulting policy. To address this, novel algorithms have been developed that mitigate overestimation bias by employing multiple Q-functions. Edge scenarios, which prioritize privacy, have recently gained prominence. In these settings, limited computational resources pose a significant challenge for complex Machine Learning approaches, making the efficiency of algorithms crucial for their performance. In this work, we introduce a novel Reinforcement Learning algorithm tailored for edge scenarios, called Edge Delayed Deep Deterministic Policy Gradient (EdgeD3). EdgeD3 enhances the Deep Deterministic Policy Gradient (DDPG) algorithm, achieving significantly improved performance with $25\%$ less Graphics Process Unit (GPU) time while maintaining the same memory usage. Additionally, EdgeD3 consistently matches or surpasses the performance of state-of-the-art methods across various benchmarks, all while using $30\%$ fewer computational resources and requiring $30\%$ less memory.

Learning control of underactuated double pendulum with Model-Based Reinforcement Learning

This report describes our proposed solution for the second AI Olympics competition held at IROS 2024. Our solution is based on a recent Model-Based Reinforcement Learning algorithm named MC-PILCO. Besides briefly reviewing the algorithm, we discuss the most critical aspects of the MC-PILCO implementation in the tasks at hand.

AI Olympics challenge with Evolutionary Soft Actor Critic

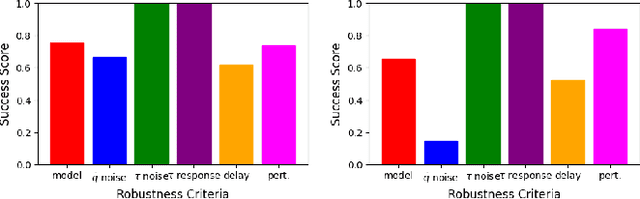
In the following report, we describe the solution we propose for the AI Olympics competition held at IROS 2024. Our solution is based on a Model-free Deep Reinforcement Learning approach combined with an evolutionary strategy. We will briefly describe the algorithms that have been used and then provide details of the approach

Adaptive Robust Controller for handling Unknown Uncertainty of Robotic Manipulators

The ability to achieve precise and smooth trajectory tracking is crucial for ensuring the successful execution of various tasks involving robotic manipulators. State-of-the-art techniques require accurate mathematical models of the robot dynamics, and robustness to model uncertainties is achieved by relying on precise bounds on the model mismatch. In this paper, we propose a novel adaptive robust feedback linearization scheme able to compensate for model uncertainties without any a-priori knowledge on them, and we provide a theoretical proof of convergence under mild assumptions. We evaluate the method on a simulated RR robot. First, we consider a nominal model with known model mismatch, which allows us to compare our strategy with state-of-the-art uncertainty-aware methods. Second, we implement the proposed control law in combination with a learned model, for which uncertainty bounds are not available. Results show that our method leads to performance comparable to uncertainty-aware methods while requiring less prior knowledge.