Modeling and Topology Estimation of Low Rank Dynamical Networks

Conventional topology learning methods for dynamical networks become inapplicable to processes exhibiting low-rank characteristics. To address this, we propose the low rank dynamical network model which ensures identifiability. By employing causal Wiener filtering, we establish a necessary and sufficient condition that links the sparsity pattern of the filter to conditional Granger causality. Building on this theoretical result, we develop a consistent method for estimating all network edges. Simulation results demonstrate the parsimony of the proposed framework and consistency of the topology estimation approach.

ARMAX identification of low rank graphical models

In large-scale systems, complex internal relationships are often present. Such interconnected systems can be effectively described by low rank stochastic processes. When identifying a predictive model of low rank processes from sampling data, the rank-deficient property of spectral densities is often obscured by the inevitable measurement noise in practice. However, existing low rank identification approaches often did not take noise into explicit consideration, leading to non-negligible inaccuracies even under weak noise. In this paper, we address the identification issue of low rank processes under measurement noise. We find that the noisy measurement model admits a sparse plus low rank structure in latent-variable graphical models. Specifically, we first decompose the problem into a maximum entropy covariance extension problem, and a low rank graphical estimation problem based on an autoregressive moving-average with exogenous input (ARMAX) model. To identify the ARMAX low rank graphical models, we propose an estimation approach based on maximum likelihood. The identifiability and consistency of this approach are proven under certain conditions. Simulation results confirm the reliable performance of the entire algorithm in both the parameter estimation and noisy data filtering.

Dealing with Collinearity in Large-Scale Linear System Identification Using Gaussian Regression

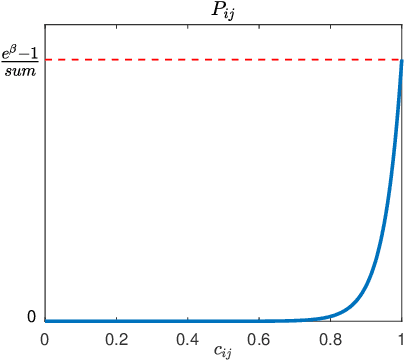
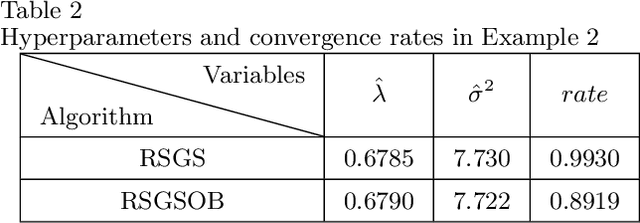
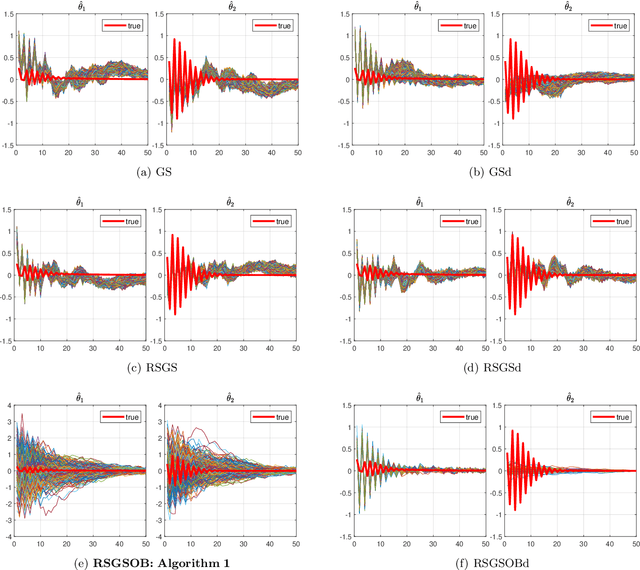
Many problems arising in control require the determination of a mathematical model of the application. This has often to be performed starting from input-output data, leading to a task known as system identification in the engineering literature. One emerging topic in this field is estimation of networks consisting of several interconnected dynamic systems. We consider the linear setting assuming that system outputs are the result of many correlated inputs, hence making system identification severely ill-conditioned. This is a scenario often encountered when modeling complex cybernetics systems composed by many sub-units with feedback and algebraic loops. We develop a strategy cast in a Bayesian regularization framework where any impulse response is seen as realization of a zero-mean Gaussian process. Any covariance is defined by the so called stable spline kernel which includes information on smooth exponential decay. We design a novel Markov chain Monte Carlo scheme able to reconstruct the impulse responses posterior by efficiently dealing with collinearity. Our scheme relies on a variation of the Gibbs sampling technique: beyond considering blocks forming a partition of the parameter space, some other (overlapping) blocks are also updated on the basis of the level of collinearity of the system inputs. Theoretical properties of the algorithm are studied obtaining its convergence rate. Numerical experiments are included using systems containing hundreds of impulse responses and highly correlated inputs.

Dealing with collinearity in large-scale linear system identification using Bayesian regularization

We consider the identification of large-scale linear and stable dynamic systems whose outputs may be the result of many correlated inputs. Hence, severe ill-conditioning may affect the estimation problem. This is a scenario often arising when modeling complex physical systems given by the interconnection of many sub-units where feedback and algebraic loops can be encountered. We develop a strategy based on Bayesian regularization where any impulse response is modeled as the realization of a zero-mean Gaussian process. The stable spline covariance is used to include information on smooth exponential decay of the impulse responses. We then design a new Markov chain Monte Carlo scheme that deals with collinearity and is able to efficiently reconstruct the posterior of the impulse responses. It is based on a variation of Gibbs sampling which updates possibly overlapping blocks of the parameter space on the basis of the level of collinearity affecting the different inputs. Numerical experiments are included to test the goodness of the approach where hundreds of impulse responses form the system and inputs correlation may be very high.

A Comparative Measurement Study of Deep Learning as a Service Framework

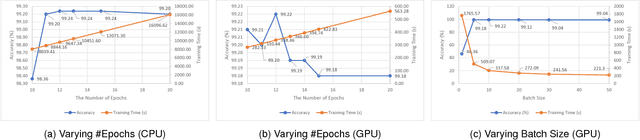
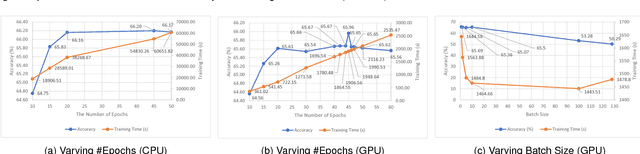
Big data powered Deep Learning (DL) and its applications have blossomed in recent years, fueled by three technological trends: a large amount of digitized data openly accessible, a growing number of DL software frameworks in open source and commercial markets, and a selection of affordable parallel computing hardware devices. However, no single DL framework, to date, dominates in terms of performance and accuracy even for baseline classification tasks on standard datasets, making the selection of a DL framework an overwhelming task. This paper takes a holistic approach to conduct empirical comparison and analysis of four representative DL frameworks with three unique contributions. First, given a selection of CPU-GPU configurations, we show that for a specific DL framework, different configurations of its hyper-parameters may have significant impact on both performance and accuracy of DL applications. Second, the optimal configuration of hyper-parameters for one DL framework (e.g., TensorFlow) often does not work well for another DL framework (e.g., Caffe or Torch) under the same CPU-GPU runtime environment. Third, we also conduct a comparative measurement study on the resource consumption patterns of four DL frameworks and their performance and accuracy implications, including CPU and memory usage, and their correlations to varying settings of hyper-parameters under different configuration combinations of hardware, parallel computing libraries. We argue that this measurement study provides in-depth empirical comparison and analysis of four representative DL frameworks, and offers practical guidance for service providers to deploying and delivering DL as a Service (DLaaS) and for application developers and DLaaS consumers to select the right DL frameworks for the right DL workloads.