Gaussian kernel expansion with basis functions uniformly bounded in $\mathcal{L}_{\infty}$

Kernel expansions are a topic of considerable interest in machine learning, also because of their relation to the so-called feature maps introduced in machine learning. Properties of the associated basis functions and weights (corresponding to eigenfunctions and eigenvalues in the Mercer setting) give insight into for example the structure of the associated reproducing kernel Hilbert space, the goodness of approximation schemes, the convergence rates and generalization properties of kernel machines. Recent work in the literature has derived some of these results by assuming uniformly bounded basis functions in $\mathcal{L}_\infty$. Motivated by this line of research, we investigate under this constraint all possible kernel expansions of the Gaussian kernel, one of the most widely used models in machine learning. Our main result is the construction on $\mathbb{R}^2$ of a Gaussian kernel expansion with weights in $\ell_p$ for any $p>1$. This result is optimal since we also prove that $p=1$ cannot be reached by the Gaussian kernel, nor by any of the other radial basis function kernels commonly used in the literature. A consequence for this kind of kernels is also the non-existence of Mercer expansions on $\mathbb{R}^2$, with respect to any finite measure, whose eigenfunctions all belong to a closed ball of $\mathcal{L}_\infty$.

Kernel-based function learning in dynamic and non stationary environments

One central theme in machine learning is function estimation from sparse and noisy data. An example is supervised learning where the elements of the training set are couples, each containing an input location and an output response. In the last decades, a substantial amount of work has been devoted to design estimators for the unknown function and to study their convergence to the optimal predictor, also characterizing the learning rate. These results typically rely on stationary assumptions where input locations are drawn from a probability distribution that does not change in time. In this work, we consider kernel-based ridge regression and derive convergence conditions under non stationary distributions, addressing also cases where stochastic adaption may happen infinitely often. This includes the important exploration-exploitation problems where e.g. a set of agents/robots has to monitor an environment to reconstruct a sensorial field and their movements rules are continuously updated on the basis of the acquired knowledge on the field and/or the surrounding environment.

Absolute integrability of Mercer kernels is only sufficient for RKHS stability

Reproducing kernel Hilbert spaces (RKHSs) are special Hilbert spaces in one-to-one correspondence with positive definite maps called kernels. They are widely employed in machine learning to reconstruct unknown functions from sparse and noisy data. In the last two decades, a subclass known as stable RKHSs has been also introduced in the setting of linear system identification. Stable RKHSs contain only absolutely integrable impulse responses over the positive real line. Hence, they can be adopted as hypothesis spaces to estimate linear, time-invariant and BIBO stable dynamic systems from input-output data. Necessary and sufficient conditions for RKHS stability are available in the literature and it is known that kernel absolute integrability implies stability. Working in discrete-time, in a recent work we have proved that this latter condition is only sufficient. Working in continuous-time, it is the purpose of this note to prove that the same result holds also for Mercer kernels.

On the stability test for reproducing kernel Hilbert spaces

Reproducing kernel Hilbert spaces (RKHSs) are special Hilbert spaces where all the evaluation functionals are linear and bounded. They are in one-to-one correspondence with positive definite maps called kernels. Stable RKHSs enjoy the additional property of containing only functions and absolutely integrable. Necessary and sufficient conditions for RKHS stability are known in the literature: the integral operator induced by the kernel must be bounded as map between $\mathcal{L}_{\infty}$, the space of essentially bounded (test) functions, and $\mathcal{L}_1$, the space of absolutely integrable functions. Considering Mercer (continuous) kernels in continuous-time and the entire discrete-time class, we show that the stability test can be reduced to the study of the kernel operator over test functions which assume (almost everywhere) only the values $\pm 1$. They represent the same functions needed to investigate stability of any single element in the RKHS. In this way, the RKHS stability test becomes an elegant generalization of a straightforward result concerning Bounded-Input Bounded-Output (BIBO) stability of a single linear time-invariant system.

Mathematical foundations of stable RKHSs

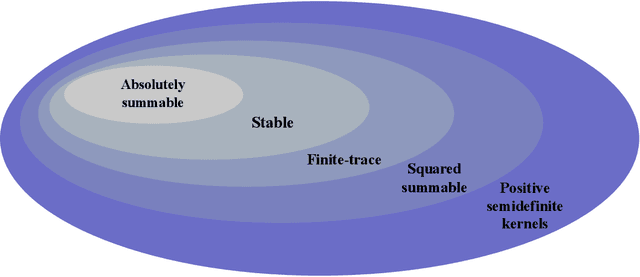
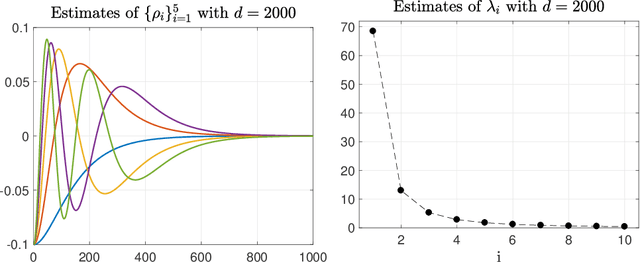
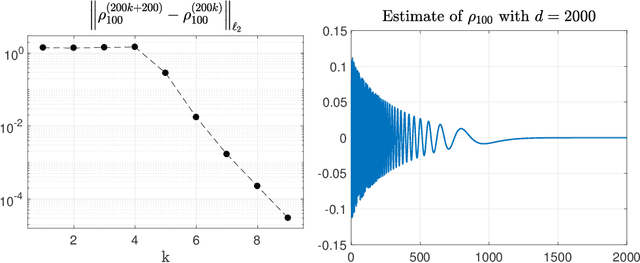
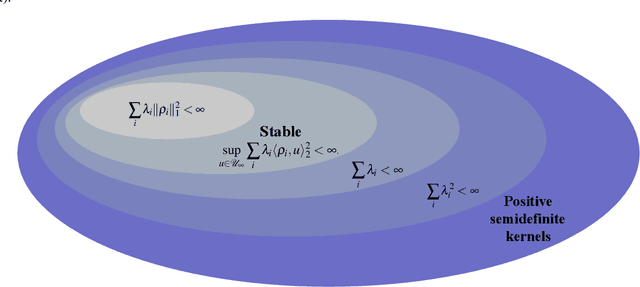
Reproducing kernel Hilbert spaces (RKHSs) are key spaces for machine learning that are becoming popular also for linear system identification. In particular, the so-called stable RKHSs can be used to model absolutely summable impulse responses. In combination e.g. with regularized least squares they can then be used to reconstruct dynamic systems from input-output data. In this paper we provide new structural properties of stable RKHSs. The relation between stable kernels and other fundamental classes, like those containing absolutely summable or finite-trace kernels, is elucidated. These insights are then brought into the feature space context. First, it is proved that any stable kernel admits feature maps induced by a basis of orthogonal eigenvectors in l2. The exact connection with classical system identification approaches that exploit such kind of functions to model impulse responses is also provided. Then, the necessary and sufficient stability condition for RKHSs designed by formulating kernel eigenvectors and eigenvalues is obtained. Overall, our new results provide novel mathematical foundations of stable RKHSs with impact on stability tests, impulse responses modeling and computational efficiency of regularized schemes for linear system identification.

Kernel absolute summability is only sufficient for RKHS stability

Regularized approaches have been successfully applied to linear system identification in recent years. Many of them model unknown impulse responses exploiting the so called Reproducing Kernel Hilbert spaces (RKHSs) that enjoy the notable property of being in one-to-one correspondence with the class of positive semidefinite kernels. The necessary and sufficient condition for a RKHS to be stable, i.e. to contain only BIBO stable linear dynamic systems, has been known in the literature at least since 2006. However, an open question still persists and concerns the equivalence of such condition with the absolute summability of the kernel. This paper provides a definite answer to this matter by proving that such correspondence does not hold. A counterexample is introduced that illustrates the existence of stable RKHSs that are induced by non-absolutely summable kernels.