A novel Multiplicative Polynomial Kernel for Volterra series identification
Paper and Code
May 20, 2019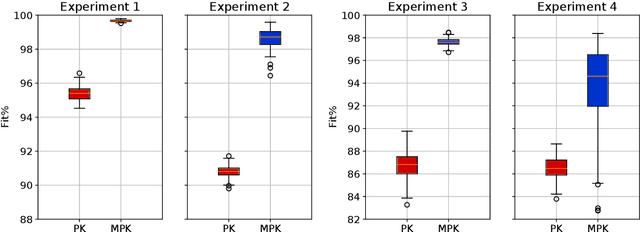
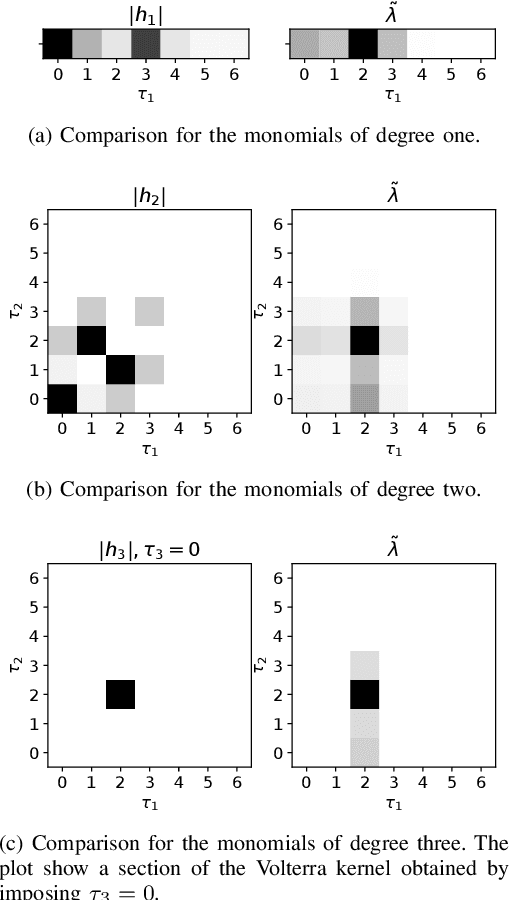
Volterra series are especially useful for nonlinear system identification, also thanks to their capability to approximate a broad range of input-output maps. However, their identification from a finite set of data is hard, due to the curse of dimensionality. Recent approaches have shown how regularized kernel-based methods can be useful for this task. In this paper, we propose a new regularization network for Volterra models identification. It relies on a new kernel given by the product of basic building blocks. Each block contains some unknown parameters that can be estimated from data using marginal likelihood optimization. In comparison with other algorithms proposed in the literature, numerical experiments show that our approach allows to better select the monomials that really influence the system output, much increasing the prediction capability of the model.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge