Learning linear modules in a dynamic network with missing node observations

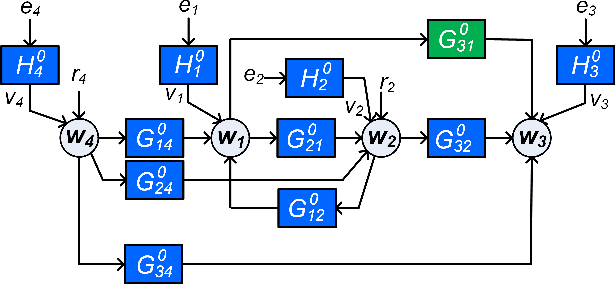
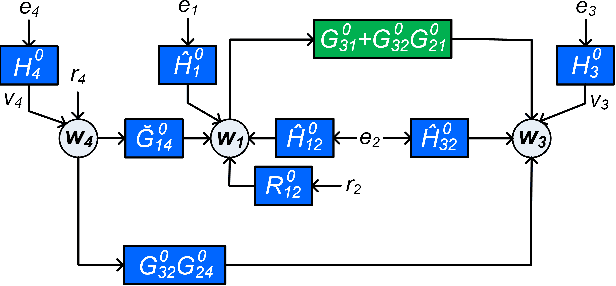
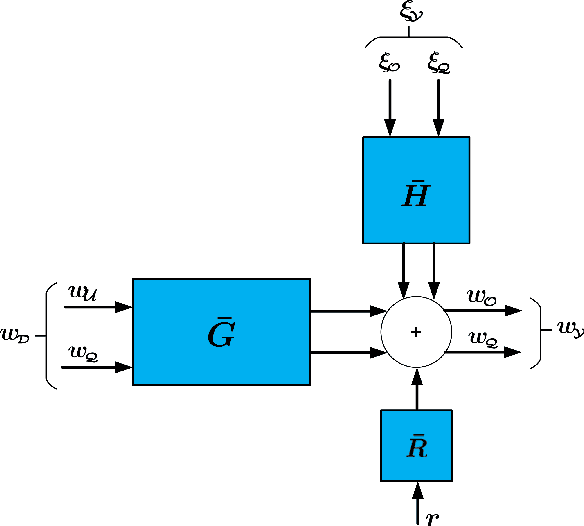
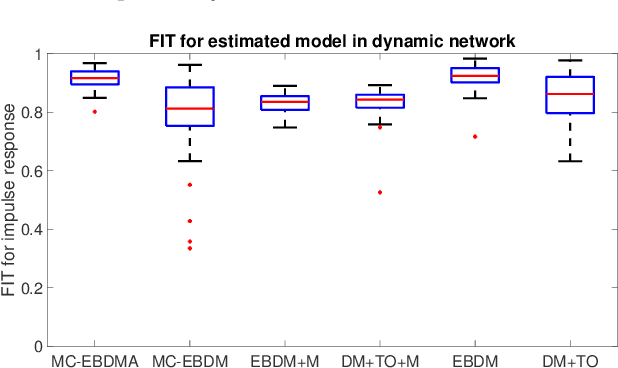
In order to identify a system (module) embedded in a dynamic network, one has to formulate a multiple-input estimation problem that necessitates certain nodes to be measured and included as predictor inputs. However, some of these nodes may not be measurable in many practical cases due to sensor selection and placement issues. This may result in biased estimates of the target module. Furthermore, the identification problem associated with the multiple-input structure may require determining a large number of parameters that are not of particular interest to the experimenter, with increased computational complexity in large-sized networks. In this paper, we tackle these problems by using a data augmentation strategy that allows us to reconstruct the missing node measurements and increase the accuracy of the estimated target module. To this end, we develop a system identification method using regularized kernel-based methods coupled with approximate inference methods. Keeping a parametric model for the module of interest, we model the other modules as Gaussian Processes (GP) with a kernel given by the so-called stable spline kernel. An Empirical Bayes (EB) approach is used to estimate the parameters of the target module. The related optimization problem is solved using an Expectation-Maximization (EM) method, where we employ a Markov-chain Monte Carlo (MCMC) technique to reconstruct the unknown missing node information and the network dynamics. Numerical simulations on dynamic network examples illustrate the potentials of the developed method.

A scalable multi-step least squares method for network identification with unknown disturbance topology

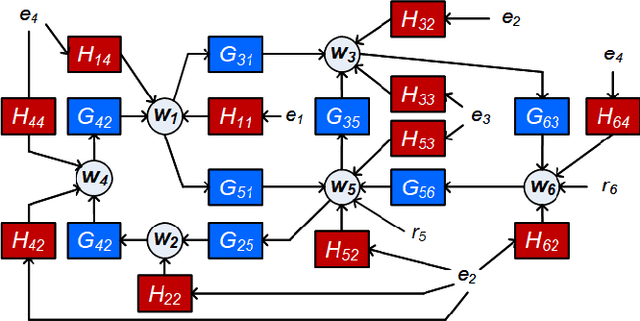
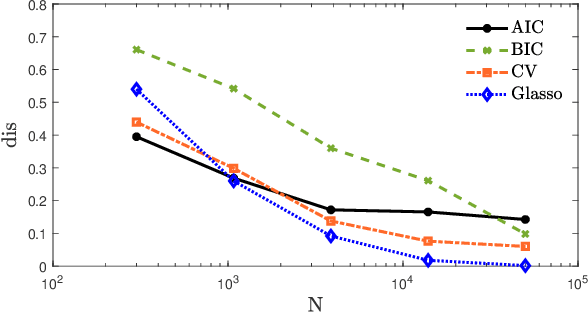
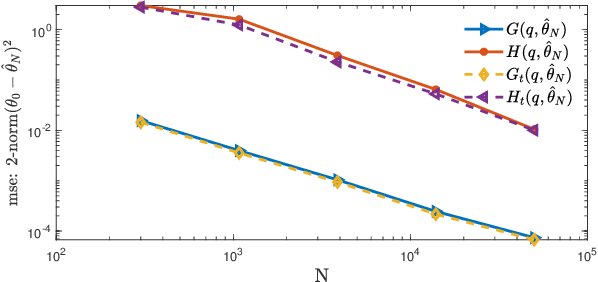
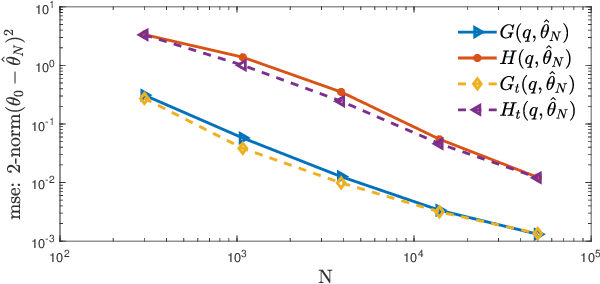
Identification methods for dynamic networks typically require prior knowledge of the network and disturbance topology, and often rely on solving poorly scalable non-convex optimization problems. While methods for estimating network topology are available in the literature, less attention has been paid to estimating the disturbance topology, i.e., the (spatial) noise correlation structure and the noise rank. In this work we present an identification method for dynamic networks, in which an estimation of the disturbance topology precedes the identification of the full dynamic network with known network topology. To this end we extend the multi-step Sequential Linear Regression and Weighted Null Space Fitting methods to deal with reduced rank noise, and use these methods to estimate the disturbance topology and the network dynamics. As a result, we provide a multi-step least squares algorithm with parallel computation capabilities and that rely only on explicit analytical solutions, thereby avoiding the usual non-convex optimizations involved. Consequently we consistently estimate dynamic networks of Box Jenkins model structure, while keeping the computational burden low. We provide a consistency proof that includes path-based data informativity conditions for allocation of excitation signals in the experimental design. Numerical simulations performed on a dynamic network with reduced rank noise clearly illustrate the potential of this method.

A frequency domain approach for local module identification in dynamic networks

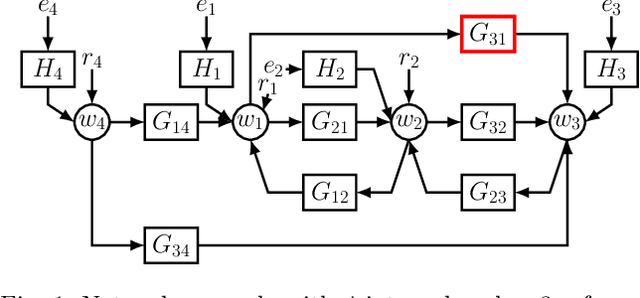
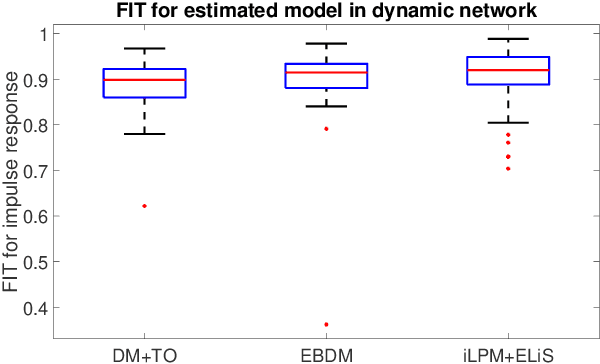
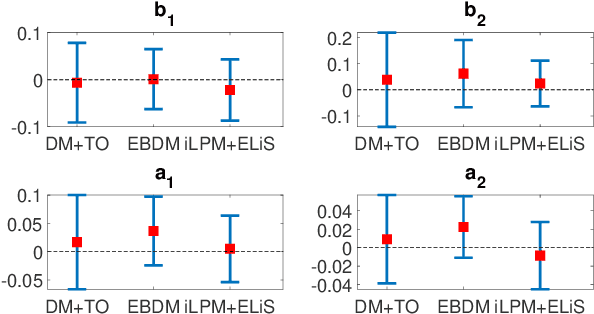
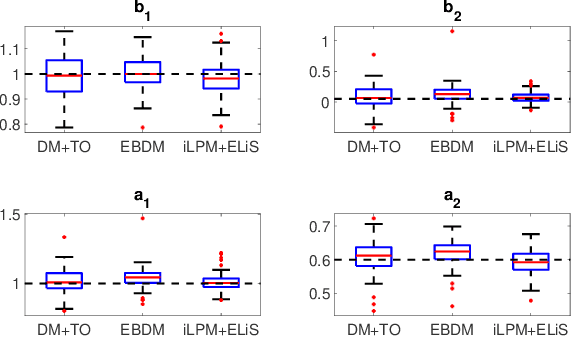
In classical approaches of dynamic network identification, in order to identify a system (module) embedded in a dynamic network, one has to formulate a Multi-input-Single-output (MISO) identification problem that requires identification of a parametric model for all the modules constituting the MISO setup including (possibly) the noise model, and determine their model order. This requirement leads to model order selection steps for modules that are of no interest to the experimenter which increases the computational complexity for large-sized networks. Also, identification using a parametric noise model (like BJ method) can suffer from local minima, however neglecting the noise model has its impact on the variance of the estimates. In this paper, we provide a two-step identification approach to avoid these problems. The first step involves performing a non-parametric indirect approach for a MISO identification problem to get the non-parametric frequency response function (FRF) estimates and its variance as a function of frequency. In the second step, the estimated non-parametric FRF of the target module is smoothed using a parametric frequency domain estimator with the estimated variance from the previous step as the non-parametric noise model. The developed approach is practical with weak assumptions on noise, uses the available toolbox, requires a parametric model only for the target module of interest, and uses a non-parametric noise model to reduce the variance of the estimates. Numerical simulations illustrate the potentials of the introduced method in comparison with the classical identification methods.