Decoupling multivariate functions using a nonparametric filtered tensor decomposition

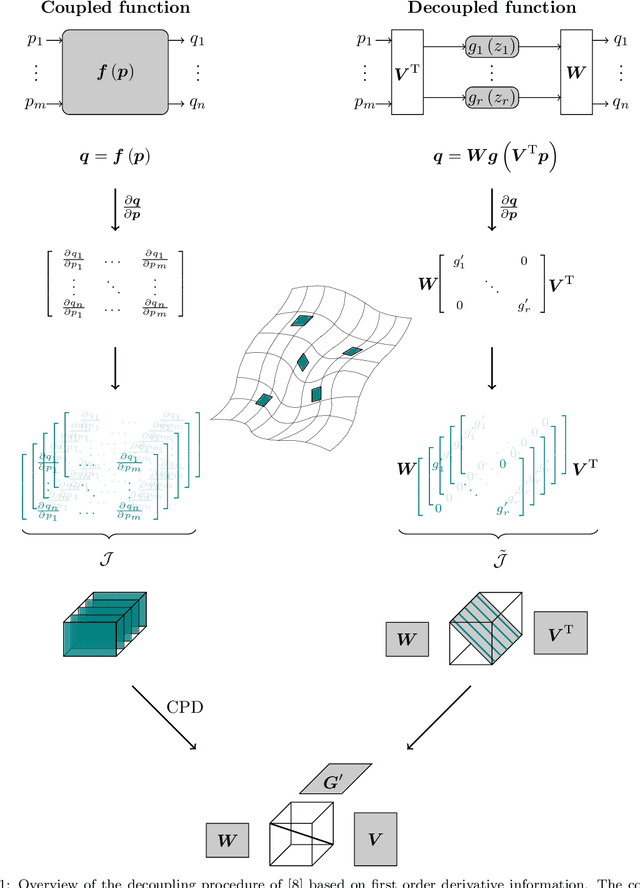
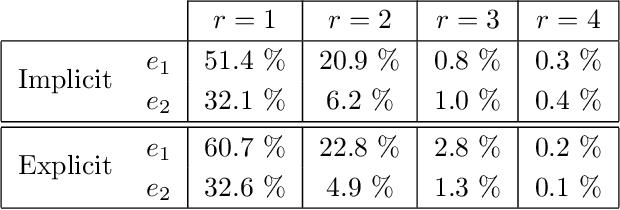
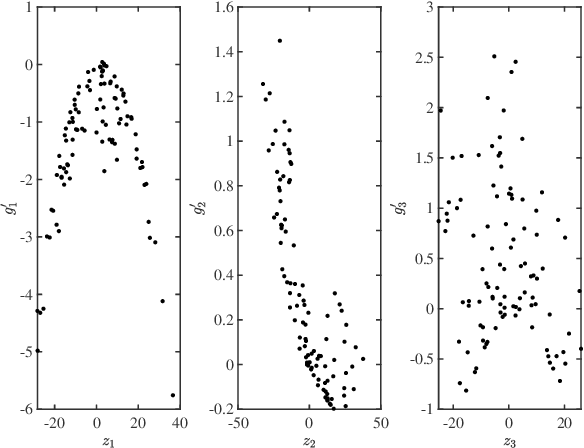
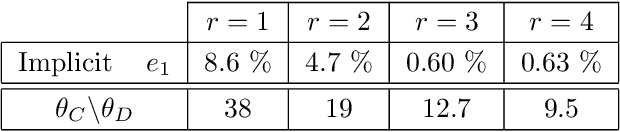
Multivariate functions emerge naturally in a wide variety of data-driven models. Popular choices are expressions in the form of basis expansions or neural networks. While highly effective, the resulting functions tend to be hard to interpret, in part because of the large number of required parameters. Decoupling techniques aim at providing an alternative representation of the nonlinearity. The so-called decoupled form is often a more efficient parameterisation of the relationship while being highly structured, favouring interpretability. In this work two new algorithms, based on filtered tensor decompositions of first order derivative information are introduced. The method returns nonparametric estimates of smooth decoupled functions. Direct applications are found in, i.a. the fields of nonlinear system identification and machine learning.

A frequency domain approach for local module identification in dynamic networks

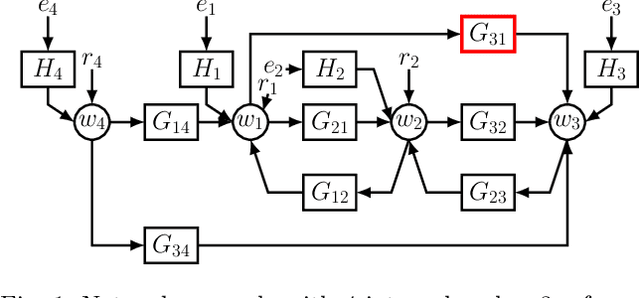
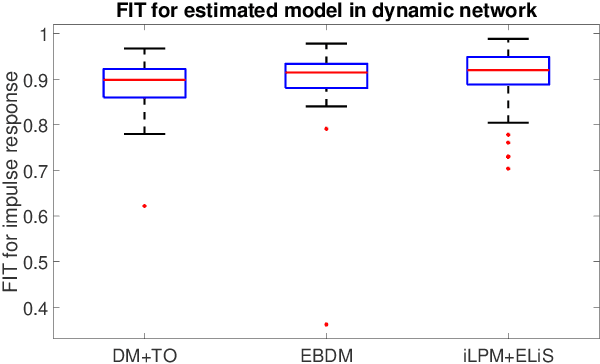
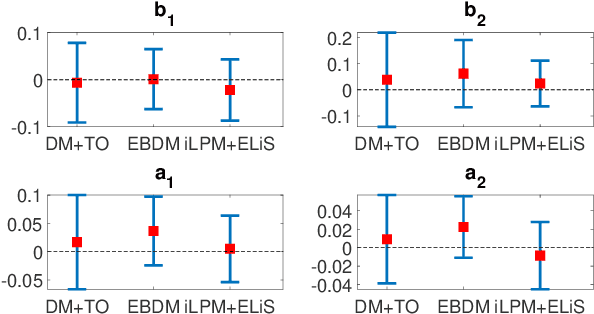
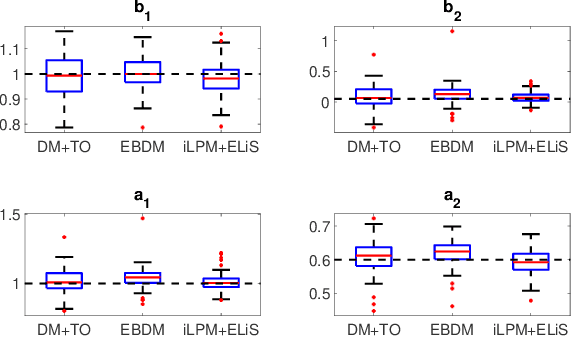
In classical approaches of dynamic network identification, in order to identify a system (module) embedded in a dynamic network, one has to formulate a Multi-input-Single-output (MISO) identification problem that requires identification of a parametric model for all the modules constituting the MISO setup including (possibly) the noise model, and determine their model order. This requirement leads to model order selection steps for modules that are of no interest to the experimenter which increases the computational complexity for large-sized networks. Also, identification using a parametric noise model (like BJ method) can suffer from local minima, however neglecting the noise model has its impact on the variance of the estimates. In this paper, we provide a two-step identification approach to avoid these problems. The first step involves performing a non-parametric indirect approach for a MISO identification problem to get the non-parametric frequency response function (FRF) estimates and its variance as a function of frequency. In the second step, the estimated non-parametric FRF of the target module is smoothed using a parametric frequency domain estimator with the estimated variance from the previous step as the non-parametric noise model. The developed approach is practical with weak assumptions on noise, uses the available toolbox, requires a parametric model only for the target module of interest, and uses a non-parametric noise model to reduce the variance of the estimates. Numerical simulations illustrate the potentials of the introduced method in comparison with the classical identification methods.