Jan Decuyper
Decoupling multivariate functions using a nonparametric filtered tensor decomposition
May 23, 2022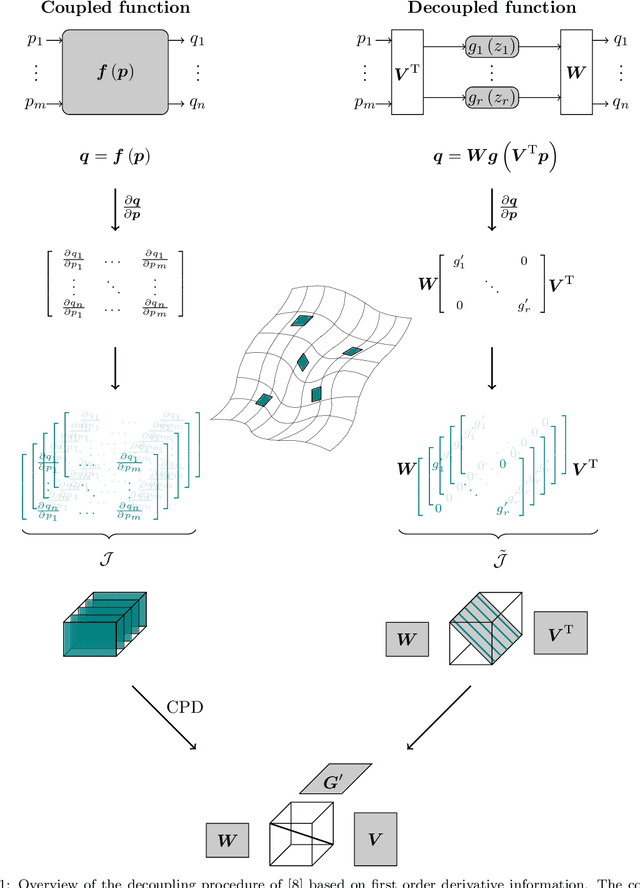
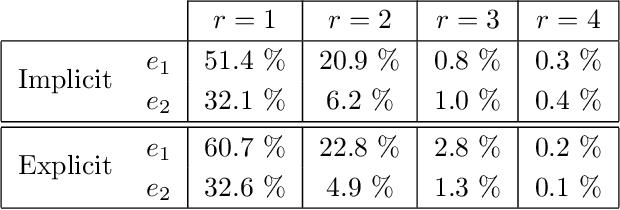
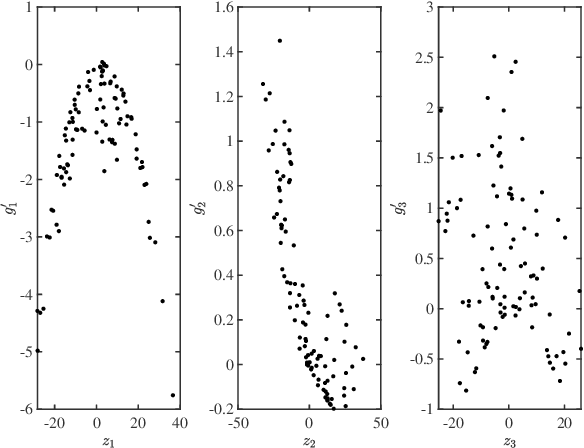
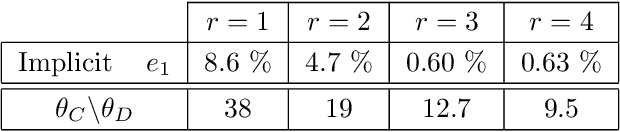
Abstract:Multivariate functions emerge naturally in a wide variety of data-driven models. Popular choices are expressions in the form of basis expansions or neural networks. While highly effective, the resulting functions tend to be hard to interpret, in part because of the large number of required parameters. Decoupling techniques aim at providing an alternative representation of the nonlinearity. The so-called decoupled form is often a more efficient parameterisation of the relationship while being highly structured, favouring interpretability. In this work two new algorithms, based on filtered tensor decompositions of first order derivative information are introduced. The method returns nonparametric estimates of smooth decoupled functions. Direct applications are found in, i.a. the fields of nonlinear system identification and machine learning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge