Unifying Controller Design for Stabilizing Nonlinear Systems with Norm-Bounded Control Inputs

This paper revisits a classical challenge in the design of stabilizing controllers for nonlinear systems with a norm-bounded input constraint. By extending Lin-Sontag's universal formula and introducing a generic (state-dependent) scaling term, a unifying controller design method is proposed. The incorporation of this generic scaling term gives a unified controller and enables the derivation of alternative universal formulas with various favorable properties, which makes it suitable for tailored control designs to meet specific requirements and provides versatility across different control scenarios. Additionally, we present a constructive approach to determine the optimal scaling term, leading to an explicit solution to an optimization problem, named optimization-based universal formula. The resulting controller ensures asymptotic stability, satisfies a norm-bounded input constraint, and optimizes a predefined cost function. Finally, the essential properties of the unified controllers are analyzed, including smoothness, continuity at the origin, stability margin, and inverse optimality. Simulations validate the approach, showcasing its effectiveness in addressing a challenging stabilizing control problem of a nonlinear system.

Quadrotor Stabilization with Safety Guarantees: A Universal Formula Approach

Safe stabilization is a significant challenge for quadrotors, which involves reaching a goal position while avoiding obstacles. Most of the existing solutions for this problem rely on optimization-based methods, demanding substantial onboard computational resources. This paper introduces a novel approach to address this issue and provides a solution that offers fast computational capabilities tailored for onboard execution. Drawing inspiration from Sontag's universal formula, we propose an analytical control strategy that incorporates the conditions of control Lyapunov functions (CLFs) and control barrier functions (CBFs), effectively avoiding the need for solving optimization problems onboard. Moreover, we extend our approach by incorporating the concepts of input-to-state stability (ISS) and input-to-state safety (ISSf), enhancing the universal formula's capacity to effectively manage disturbances. Furthermore, we present a projection-based approach to ensure that the universal formula remains effective even when faced with control input constraints. The basic idea of this approach is to project the control input derived from the universal formula onto the closest point within the control input domain. Through comprehensive simulations and experimental results, we validate the efficacy and highlight the advantages of our methodology.

Decoupling multivariate functions using a nonparametric filtered tensor decomposition

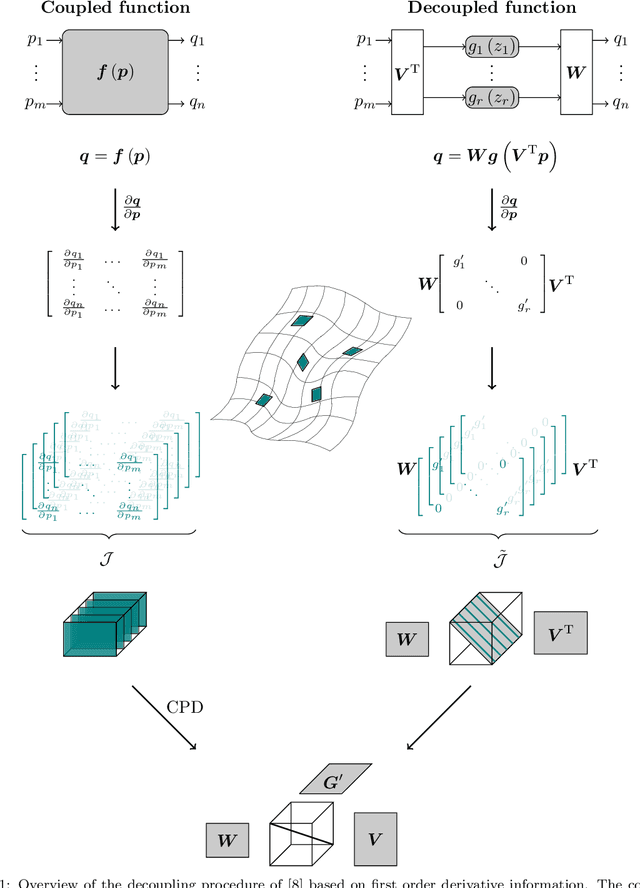
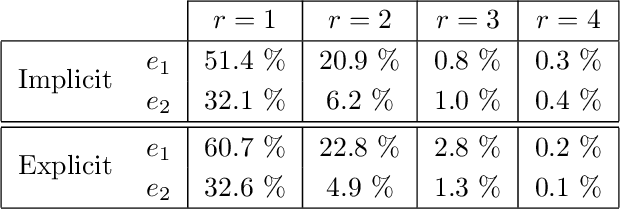
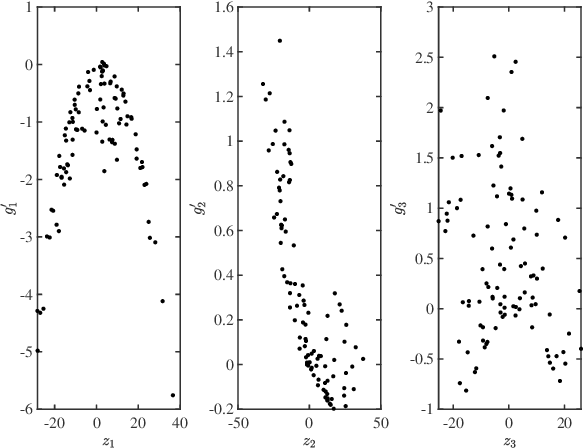
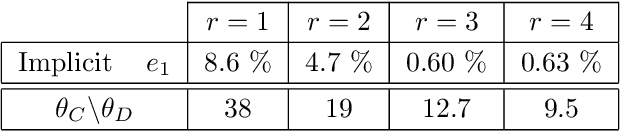
Multivariate functions emerge naturally in a wide variety of data-driven models. Popular choices are expressions in the form of basis expansions or neural networks. While highly effective, the resulting functions tend to be hard to interpret, in part because of the large number of required parameters. Decoupling techniques aim at providing an alternative representation of the nonlinearity. The so-called decoupled form is often a more efficient parameterisation of the relationship while being highly structured, favouring interpretability. In this work two new algorithms, based on filtered tensor decompositions of first order derivative information are introduced. The method returns nonparametric estimates of smooth decoupled functions. Direct applications are found in, i.a. the fields of nonlinear system identification and machine learning.