The Generalized Cross Validation Filter
Paper and Code
Jun 08, 2017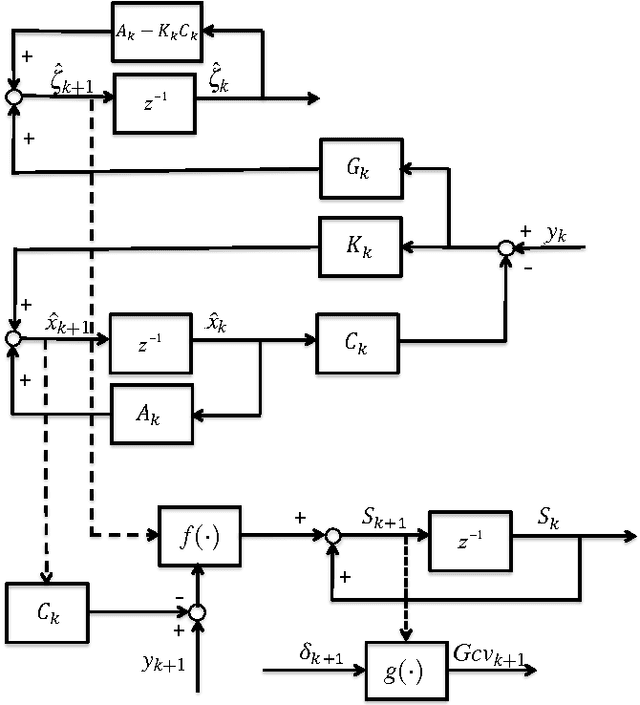
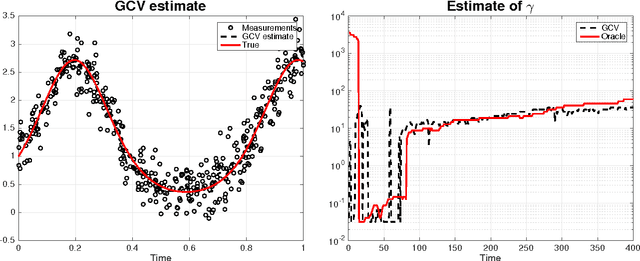
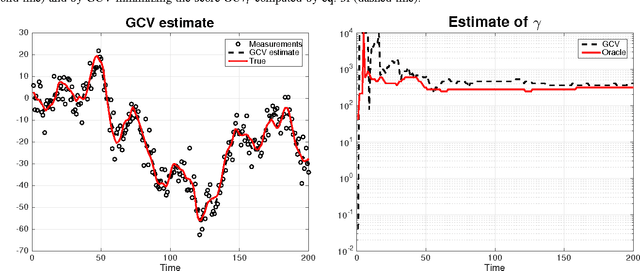
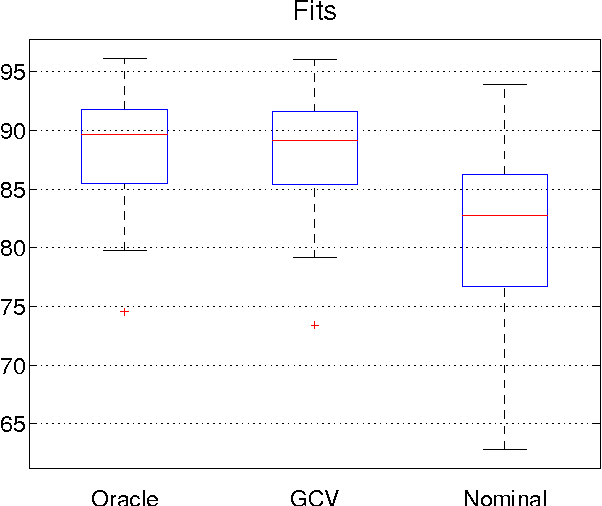
Generalized cross validation (GCV) is one of the most important approaches used to estimate parameters in the context of inverse problems and regularization techniques. A notable example is the determination of the smoothness parameter in splines. When the data are generated by a state space model, like in the spline case, efficient algorithms are available to evaluate the GCV score with complexity that scales linearly in the data set size. However, these methods are not amenable to on-line applications since they rely on forward and backward recursions. Hence, if the objective has been evaluated at time $t-1$ and new data arrive at time t, then O(t) operations are needed to update the GCV score. In this paper we instead show that the update cost is $O(1)$, thus paving the way to the on-line use of GCV. This result is obtained by deriving the novel GCV filter which extends the classical Kalman filter equations to efficiently propagate the GCV score over time. We also illustrate applications of the new filter in the context of state estimation and on-line regularized linear system identification.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge