The Klarna Product Page Dataset: A Realistic Benchmark for Web Representation Learning

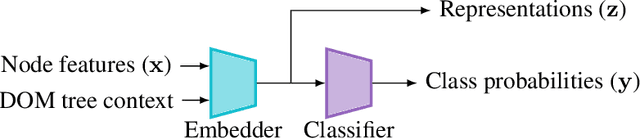
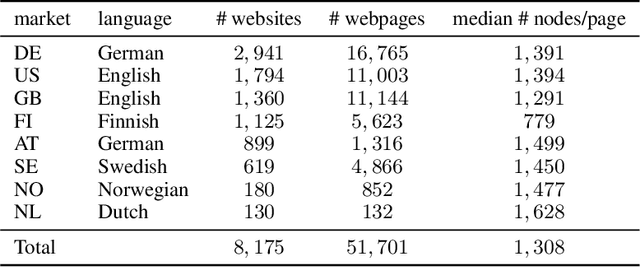
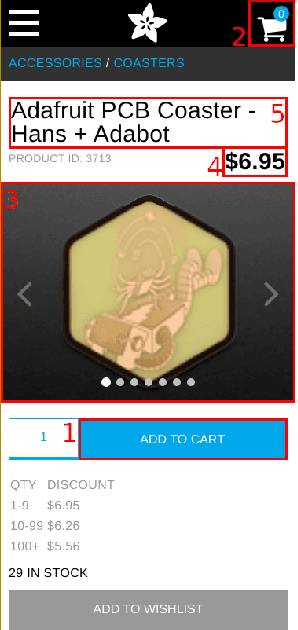
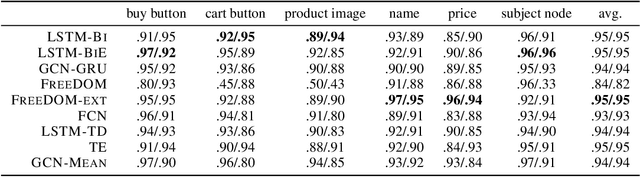
This paper tackles the under-explored problem of DOM tree element representation learning. We advance the field of machine learning-based web automation and hope to spur further research regarding this crucial area with two contributions. First, we adapt several popular Graph-based Neural Network models and apply them to embed elements in website DOM trees. Second, we present a large-scale and realistic dataset of webpages. By providing this open-access resource, we lower the entry barrier to this area of research. The dataset contains $51,701$ manually labeled product pages from $8,175$ real e-commerce websites. The pages can be rendered entirely in a web browser and are suitable for computer vision applications. This makes it substantially richer and more diverse than other datasets proposed for element representation learning, classification and prediction on the web. Finally, using our proposed dataset, we show that the embeddings produced by a Graph Convolutional Neural Network outperform representations produced by other state-of-the-art methods in a web element prediction task.

Parameter elimination in particle Gibbs sampling

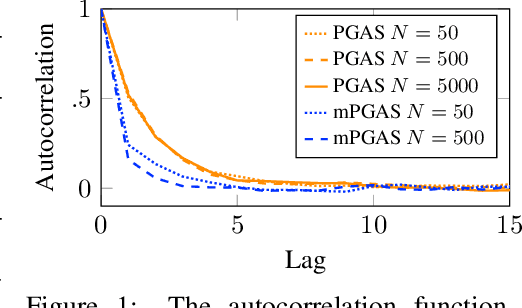
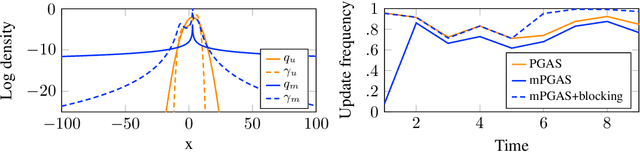
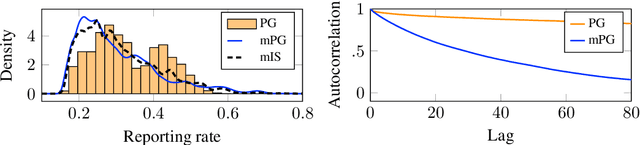
Bayesian inference in state-space models is challenging due to high-dimensional state trajectories. A viable approach is particle Markov chain Monte Carlo, combining MCMC and sequential Monte Carlo to form "exact approximations" to otherwise intractable MCMC methods. The performance of the approximation is limited to that of the exact method. We focus on particle Gibbs and particle Gibbs with ancestor sampling, improving their performance beyond that of the underlying Gibbs sampler (which they approximate) by marginalizing out one or more parameters. This is possible when the parameter prior is conjugate to the complete data likelihood. Marginalization yields a non-Markovian model for inference, but we show that, in contrast to the general case, this method still scales linearly in time. While marginalization can be cumbersome to implement, recent advances in probabilistic programming have enabled its automation. We demonstrate how the marginalized methods are viable as efficient inference backends in probabilistic programming, and demonstrate with examples in ecology and epidemiology.

On the estimation of initial conditions in kernel-based system identification

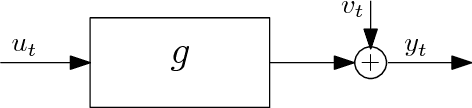
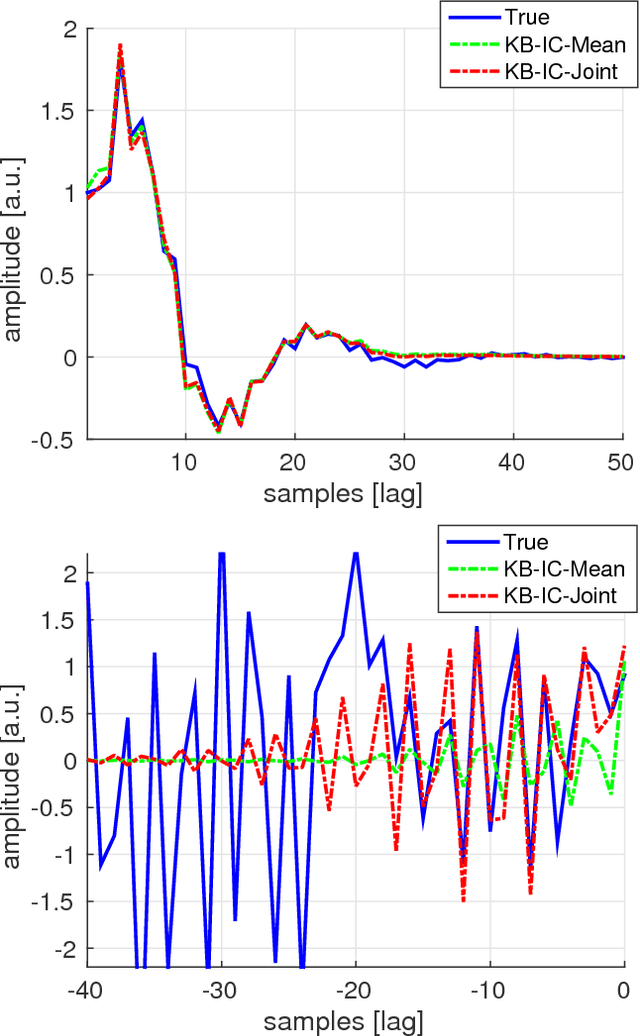
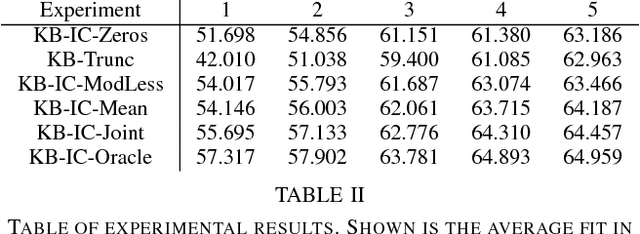
Recent developments in system identification have brought attention to regularized kernel-based methods, where, adopting the recently introduced stable spline kernel, prior information on the unknown process is enforced. This reduces the variance of the estimates and thus makes kernel-based methods particularly attractive when few input-output data samples are available. In such cases however, the influence of the system initial conditions may have a significant impact on the output dynamics. In this paper, we specifically address this point. We propose three methods that deal with the estimation of initial conditions using different types of information. The methods consist in various mixed maximum likelihood--a posteriori estimators which estimate the initial conditions and tune the hyperparameters characterizing the stable spline kernel. To solve the related optimization problems, we resort to the expectation-maximization method, showing that the solutions can be attained by iterating among simple update steps. Numerical experiments show the advantages, in terms of accuracy in reconstructing the system impulse response, of the proposed strategies, compared to other kernel-based schemes not accounting for the effect initial conditions.

A new kernel-based approach for overparameterized Hammerstein system identification

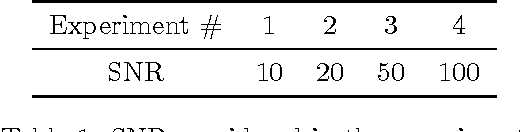
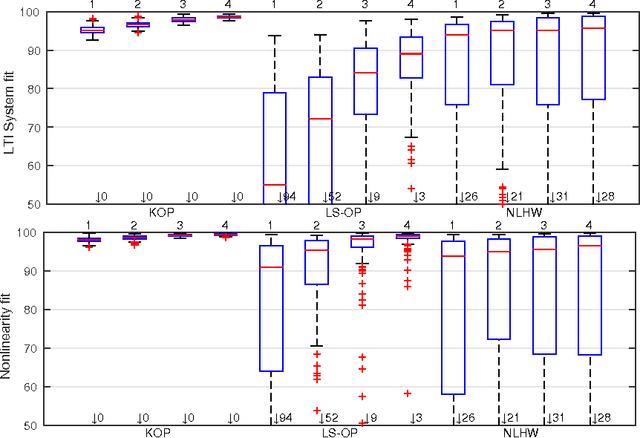
In this paper we propose a new identification scheme for Hammerstein systems, which are dynamic systems consisting of a static nonlinearity and a linear time-invariant dynamic system in cascade. We assume that the nonlinear function can be described as a linear combination of $p$ basis functions. We reconstruct the $p$ coefficients of the nonlinearity together with the first $n$ samples of the impulse response of the linear system by estimating an $np$-dimensional overparameterized vector, which contains all the combinations of the unknown variables. To avoid high variance in these estimates, we adopt a regularized kernel-based approach and, in particular, we introduce a new kernel tailored for Hammerstein system identification. We show that the resulting scheme provides an estimate of the overparameterized vector that can be uniquely decomposed as the combination of an impulse response and $p$ coefficients of the static nonlinearity. We also show, through several numerical experiments, that the proposed method compares very favorably with two standard methods for Hammerstein system identification.