Parameter elimination in particle Gibbs sampling

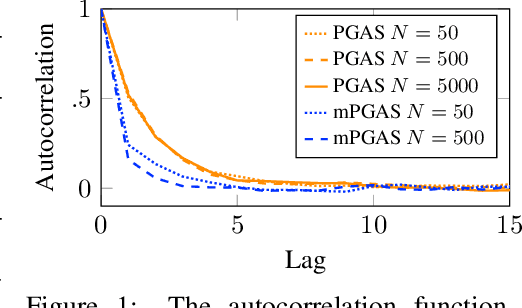
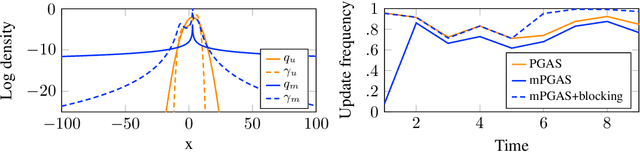
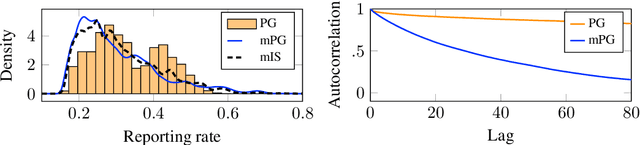
Bayesian inference in state-space models is challenging due to high-dimensional state trajectories. A viable approach is particle Markov chain Monte Carlo, combining MCMC and sequential Monte Carlo to form "exact approximations" to otherwise intractable MCMC methods. The performance of the approximation is limited to that of the exact method. We focus on particle Gibbs and particle Gibbs with ancestor sampling, improving their performance beyond that of the underlying Gibbs sampler (which they approximate) by marginalizing out one or more parameters. This is possible when the parameter prior is conjugate to the complete data likelihood. Marginalization yields a non-Markovian model for inference, but we show that, in contrast to the general case, this method still scales linearly in time. While marginalization can be cumbersome to implement, recent advances in probabilistic programming have enabled its automation. We demonstrate how the marginalized methods are viable as efficient inference backends in probabilistic programming, and demonstrate with examples in ecology and epidemiology.

Probabilistic learning of nonlinear dynamical systems using sequential Monte Carlo

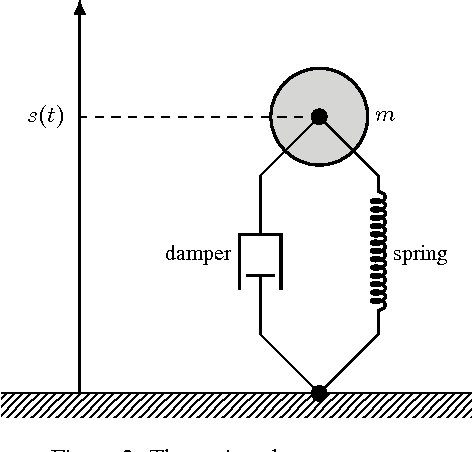
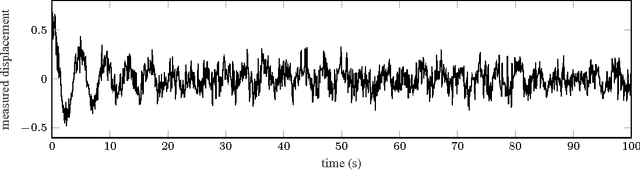
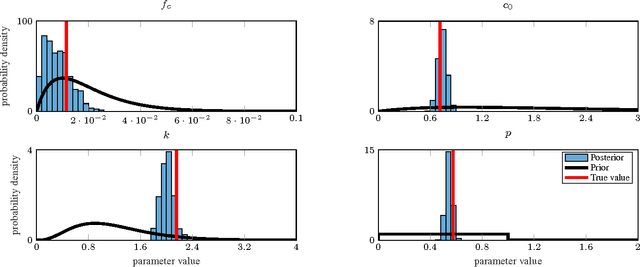
Probabilistic modeling provides the capability to represent and manipulate uncertainty in data, models, predictions and decisions. We are concerned with the problem of learning probabilistic models of dynamical systems from measured data. Specifically, we consider learning of probabilistic nonlinear state-space models. There is no closed-form solution available for this problem, implying that we are forced to use approximations. In this tutorial we will provide a self-contained introduction to one of the state-of-the-art methods---the particle Metropolis--Hastings algorithm---which has proven to offer a practical approximation. This is a Monte Carlo based method, where the particle filter is used to guide a Markov chain Monte Carlo method through the parameter space. One of the key merits of the particle Metropolis--Hastings algorithm is that it is guaranteed to converge to the "true solution" under mild assumptions, despite being based on a particle filter with only a finite number of particles. We will also provide a motivating numerical example illustrating the method using a modeling language tailored for sequential Monte Carlo methods. The intention of modeling languages of this kind is to open up the power of sophisticated Monte Carlo methods---including particle Metropolis--Hastings---to a large group of users without requiring them to know all the underlying mathematical details.