Andreas Svensson
Data Consistency Approach to Model Validation
Aug 17, 2018



Abstract:In scientific inference problems, the underlying statistical modeling assumptions have a crucial impact on the end results. There exist, however, only a few automatic means for validating these fundamental modelling assumptions. The contribution in this paper is a general criterion to evaluate the consistency of a set of statistical models with respect to observed data. This is achieved by automatically gauging the models' ability to generate data that is similar to the observed data. Importantly, the criterion follows from the model class itself and is therefore directly applicable to a broad range of inference problems with varying data types. The proposed data consistency criterion is illustrated and evaluated using three synthetic and two real data sets.
Learning dynamical systems with particle stochastic approximation EM
Jun 25, 2018



Abstract:We present the particle stochastic approximation EM (PSAEM) algorithm for learning of dynamical systems. The method builds on the EM algorithm, an iterative procedure for maximum likelihood inference in latent variable models. By combining stochastic approximation EM and particle Gibbs with ancestor sampling (PGAS), PSAEM obtains superior computational performance and convergence properties compared to plain particle-smoothing-based approximations of the EM algorithm. PSAEM can be used for plain maximum likelihood inference as well as for empirical Bayes learning of hyperparameters. Specifically, the latter point means that existing PGAS implementations easily can be extended with PSAEM to estimate hyperparameters at almost no extra computational cost. We discuss the convergence properties of the algorithm, and demonstrate it on several machine learning applications.
How consistent is my model with the data? Information-Theoretic Model Check
Dec 19, 2017



Abstract:The choice of model class is fundamental in statistical learning and system identification, no matter whether the class is derived from physical principles or is a generic black-box. We develop a method to evaluate the specified model class by assessing its capability of reproducing data that is similar to the observed data record. This model check is based on the information-theoretic properties of models viewed as data generators and is applicable to e.g. sequential data and nonlinear dynamical models. The method can be understood as a specific two-sided posterior predictive test. We apply the information-theoretic model check to both synthetic and real data and compare it with a classical whiteness test.
Probabilistic learning of nonlinear dynamical systems using sequential Monte Carlo
Dec 15, 2017
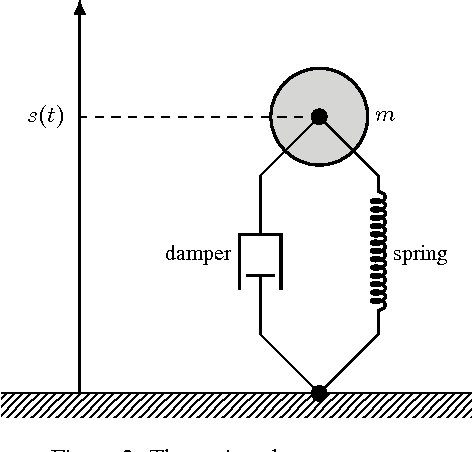
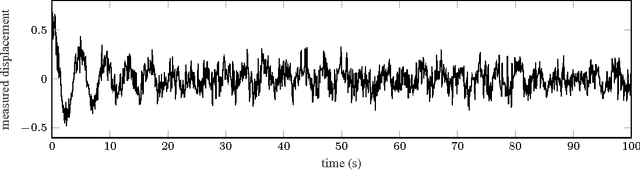
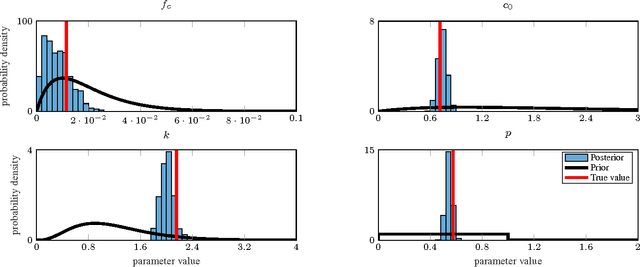
Abstract:Probabilistic modeling provides the capability to represent and manipulate uncertainty in data, models, predictions and decisions. We are concerned with the problem of learning probabilistic models of dynamical systems from measured data. Specifically, we consider learning of probabilistic nonlinear state-space models. There is no closed-form solution available for this problem, implying that we are forced to use approximations. In this tutorial we will provide a self-contained introduction to one of the state-of-the-art methods---the particle Metropolis--Hastings algorithm---which has proven to offer a practical approximation. This is a Monte Carlo based method, where the particle filter is used to guide a Markov chain Monte Carlo method through the parameter space. One of the key merits of the particle Metropolis--Hastings algorithm is that it is guaranteed to converge to the "true solution" under mild assumptions, despite being based on a particle filter with only a finite number of particles. We will also provide a motivating numerical example illustrating the method using a modeling language tailored for sequential Monte Carlo methods. The intention of modeling languages of this kind is to open up the power of sophisticated Monte Carlo methods---including particle Metropolis--Hastings---to a large group of users without requiring them to know all the underlying mathematical details.
Learning of state-space models with highly informative observations: a tempered Sequential Monte Carlo solution
Dec 13, 2017



Abstract:Probabilistic (or Bayesian) modeling and learning offers interesting possibilities for systematic representation of uncertainty using probability theory. However, probabilistic learning often leads to computationally challenging problems. Some problems of this type that were previously intractable can now be solved on standard personal computers thanks to recent advances in Monte Carlo methods. In particular, for learning of unknown parameters in nonlinear state-space models, methods based on the particle filter (a Monte Carlo method) have proven very useful. A notoriously challenging problem, however, still occurs when the observations in the state-space model are highly informative, i.e. when there is very little or no measurement noise present, relative to the amount of process noise. The particle filter will then struggle in estimating one of the basic components for probabilistic learning, namely the likelihood $p($data$|$parameters$)$. To this end we suggest an algorithm which initially assumes that there is substantial amount of artificial measurement noise present. The variance of this noise is sequentially decreased in an adaptive fashion such that we, in the end, recover the original problem or possibly a very close approximation of it. The main component in our algorithm is a sequential Monte Carlo (SMC) sampler, which gives our proposed method a clear resemblance to the SMC^2 method. Another natural link is also made to the ideas underlying the approximate Bayesian computation (ABC). We illustrate it with numerical examples, and in particular show promising results for a challenging Wiener-Hammerstein benchmark problem.
A flexible state space model for learning nonlinear dynamical systems
Mar 28, 2017



Abstract:We consider a nonlinear state-space model with the state transition and observation functions expressed as basis function expansions. The coefficients in the basis function expansions are learned from data. Using a connection to Gaussian processes we also develop priors on the coefficients, for tuning the model flexibility and to prevent overfitting to data, akin to a Gaussian process state-space model. The priors can alternatively be seen as a regularization, and helps the model in generalizing the data without sacrificing the richness offered by the basis function expansion. To learn the coefficients and other unknown parameters efficiently, we tailor an algorithm using state-of-the-art sequential Monte Carlo methods, which comes with theoretical guarantees on the learning. Our approach indicates promising results when evaluated on a classical benchmark as well as real data.
Computationally Efficient Bayesian Learning of Gaussian Process State Space Models
Apr 15, 2016



Abstract:Gaussian processes allow for flexible specification of prior assumptions of unknown dynamics in state space models. We present a procedure for efficient Bayesian learning in Gaussian process state space models, where the representation is formed by projecting the problem onto a set of approximate eigenfunctions derived from the prior covariance structure. Learning under this family of models can be conducted using a carefully crafted particle MCMC algorithm. This scheme is computationally efficient and yet allows for a fully Bayesian treatment of the problem. Compared to conventional system identification tools or existing learning methods, we show competitive performance and reliable quantification of uncertainties in the model.
Sequential Monte Carlo Methods for System Identification
Mar 10, 2016
Abstract:One of the key challenges in identifying nonlinear and possibly non-Gaussian state space models (SSMs) is the intractability of estimating the system state. Sequential Monte Carlo (SMC) methods, such as the particle filter (introduced more than two decades ago), provide numerical solutions to the nonlinear state estimation problems arising in SSMs. When combined with additional identification techniques, these algorithms provide solid solutions to the nonlinear system identification problem. We describe two general strategies for creating such combinations and discuss why SMC is a natural tool for implementing these strategies.
Marginalizing Gaussian Process Hyperparameters using Sequential Monte Carlo
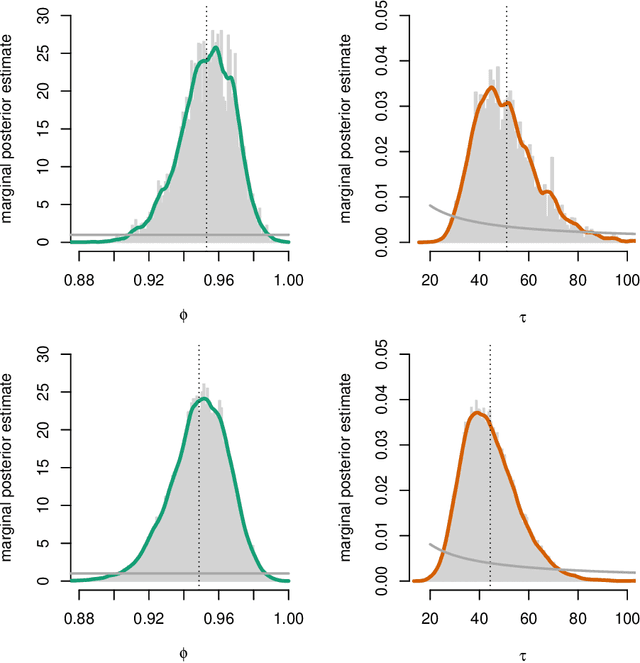
Oct 02, 2015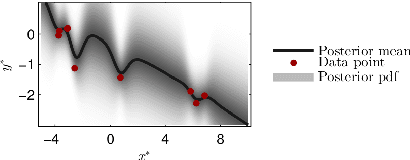
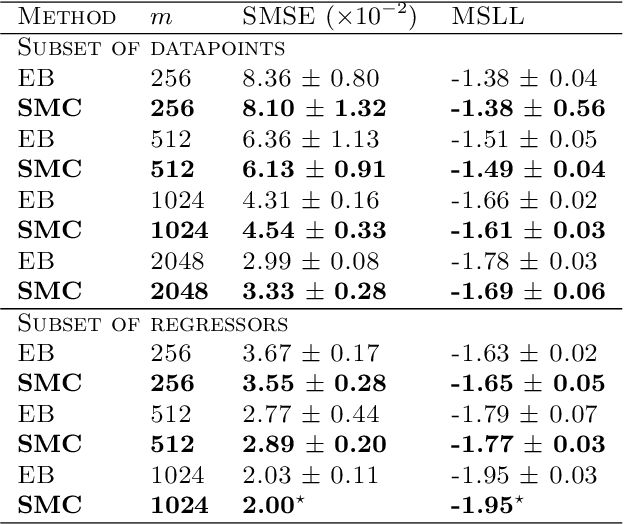
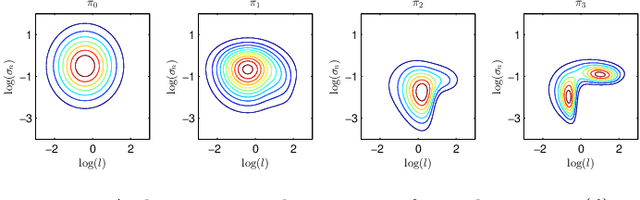
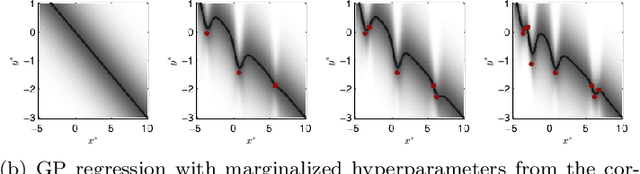
Abstract:Gaussian process regression is a popular method for non-parametric probabilistic modeling of functions. The Gaussian process prior is characterized by so-called hyperparameters, which often have a large influence on the posterior model and can be difficult to tune. This work provides a method for numerical marginalization of the hyperparameters, relying on the rigorous framework of sequential Monte Carlo. Our method is well suited for online problems, and we demonstrate its ability to handle real-world problems with several dimensions and compare it to other marginalization methods. We also conclude that our proposed method is a competitive alternative to the commonly used point estimates maximizing the likelihood, both in terms of computational load and its ability to handle multimodal posteriors.
Identification of jump Markov linear models using particle filters
Sep 25, 2014

Abstract:Jump Markov linear models consists of a finite number of linear state space models and a discrete variable encoding the jumps (or switches) between the different linear models. Identifying jump Markov linear models makes for a challenging problem lacking an analytical solution. We derive a new expectation maximization (EM) type algorithm that produce maximum likelihood estimates of the model parameters. Our development hinges upon recent progress in combining particle filters with Markov chain Monte Carlo methods in solving the nonlinear state smoothing problem inherent in the EM formulation. Key to our development is that we exploit a conditionally linear Gaussian substructure in the model, allowing for an efficient algorithm.
* Accepted to 53rd IEEE International Conference on Decision and Control (CDC), 2014 (Los Angeles, CA, USA)
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge