Robust Semi-Supervised Learning when Labels are Missing at Random

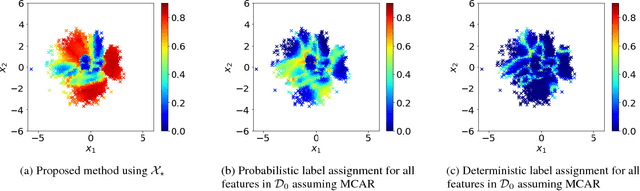
Semi-supervised learning methods are motivated by the relative paucity of labeled data and aim to utilize large sources of unlabeled data to improve predictive tasks. It has been noted, however, such improvements are not guaranteed in general in some cases the unlabeled data impairs the performance. A fundamental source of error comes from restrictive assumptions about the unlabeled features. In this paper, we develop a semi-supervised learning approach that relaxes such assumptions and is robust with respect to labels missing at random. The approach ensures that uncertainty about the classes is propagated to the unlabeled features in a robust manner. It is applicable using any generative model with associated learning algorithm. We illustrate the approach using both standard synthetic data examples and the MNIST data with unlabeled adversarial examples.

Prediction performance after learning in Gaussian process regression

This paper considers the quantification of the prediction performance in Gaussian process regression. The standard approach is to base the prediction error bars on the theoretical predictive variance, which is a lower bound on the mean square-error (MSE). This approach, however, does not take into account that the statistical model is learned from the data. We show that this omission leads to a systematic underestimation of the prediction errors. Starting from a generalization of the Cram\'er-Rao bound, we derive a more accurate MSE bound which provides a measure of uncertainty for prediction of Gaussian processes. The improved bound is easily computed and we illustrate it using synthetic and real data examples. of uncertainty for prediction of Gaussian processes and illustrate it using synthetic and real data examples.

Sequential Monte Carlo Methods for System Identification

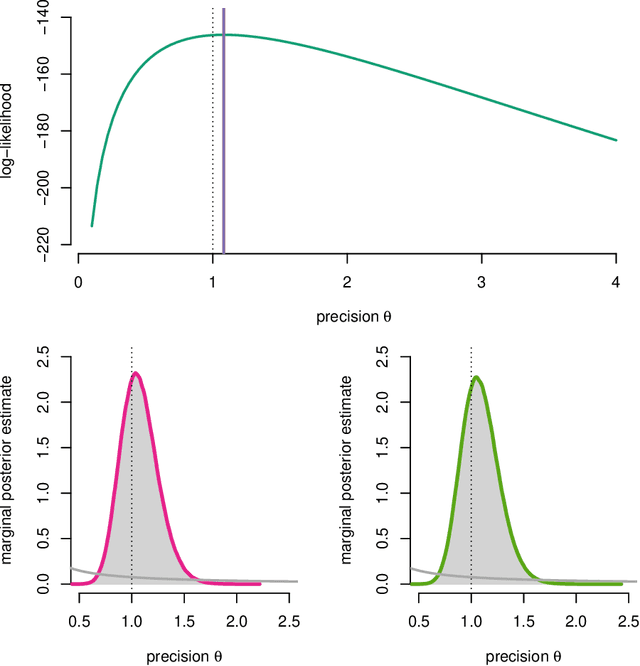
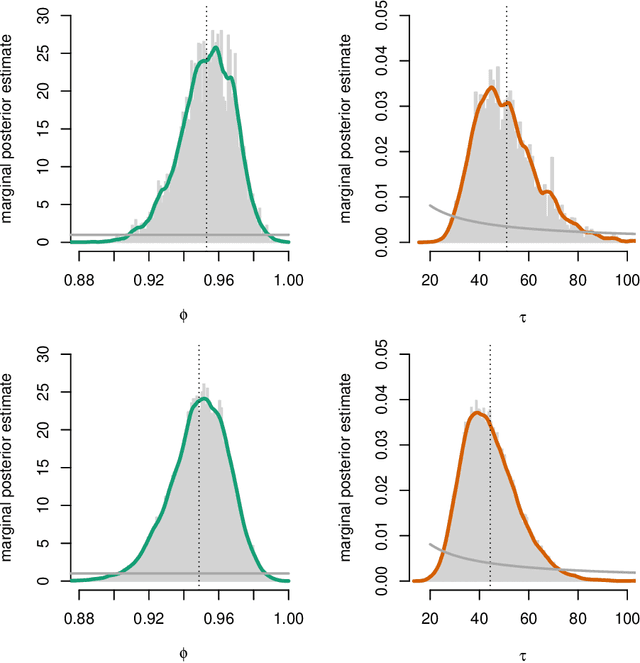
One of the key challenges in identifying nonlinear and possibly non-Gaussian state space models (SSMs) is the intractability of estimating the system state. Sequential Monte Carlo (SMC) methods, such as the particle filter (introduced more than two decades ago), provide numerical solutions to the nonlinear state estimation problems arising in SSMs. When combined with additional identification techniques, these algorithms provide solid solutions to the nonlinear system identification problem. We describe two general strategies for creating such combinations and discuss why SMC is a natural tool for implementing these strategies.