Real-Time Robotic Search using Hierarchical Spatial Point Processes

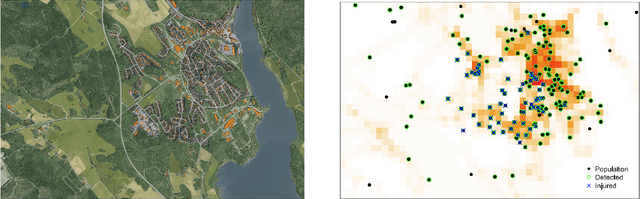
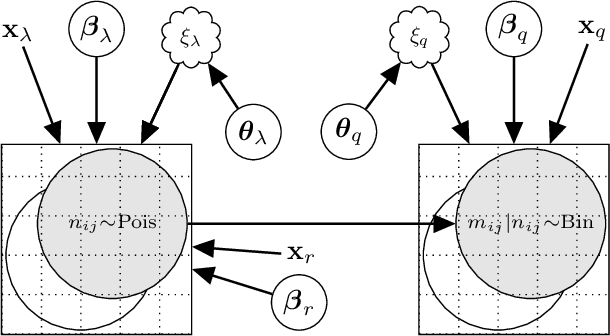
Aerial robots hold great potential for aiding Search and Rescue (SAR) efforts over large areas. Traditional approaches typically searches an area exhaustively, thereby ignoring that the density of victims varies based on predictable factors, such as the terrain, population density and the type of disaster. We present a probabilistic model to automate SAR planning, with explicit minimization of the expected time to discovery. The proposed model is a hierarchical spatial point process with three interacting spatial fields for i) the point patterns of persons in the area, ii) the probability of detecting persons and iii) the probability of injury. This structure allows inclusion of informative priors from e.g. geographic or cell phone traffic data, while falling back to latent Gaussian processes when priors are missing or inaccurate. To solve this problem in real-time, we propose a combination of fast approximate inference using Integrated Nested Laplace Approximation (INLA), and a novel Monte Carlo tree search tailored to the problem. Experiments using data simulated from real world GIS maps show that the framework outperforms traditional search strategies, and finds up to ten times more injured in the crucial first hours.

Correlated pseudo-marginal Metropolis-Hastings using quasi-Newton proposals

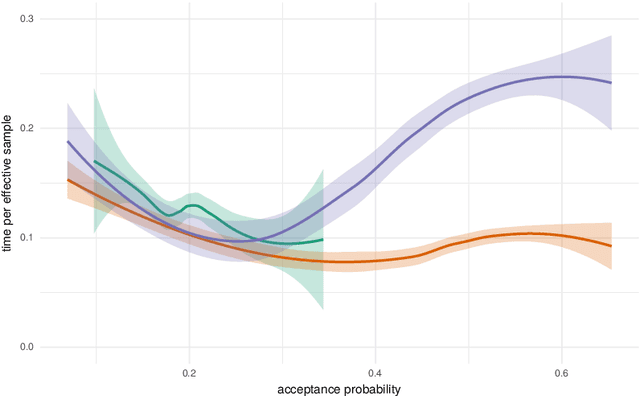
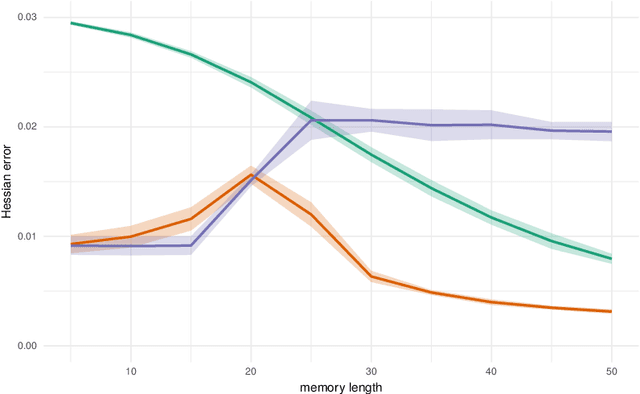
Pseudo-marginal Metropolis-Hastings (pmMH) is a versatile algorithm for sampling from target distributions which are not easy to evaluate point-wise. However, pmMH requires good proposal distributions to sample efficiently from the target, which can be problematic to construct in practice. This is especially a problem for high-dimensional targets when the standard random-walk proposal is inefficient. We extend pmMH to allow for constructing the proposal based on information from multiple past iterations. As a consequence, quasi-Newton (qN) methods can be employed to form proposals which utilize gradient information to guide the Markov chain to areas of high probability and to construct approximations of the local curvature to scale step sizes. The proposed method is demonstrated on several problems which indicate that qN proposals can perform better than other common Hessian-based proposals.

Getting Started with Particle Metropolis-Hastings for Inference in Nonlinear Dynamical Models

This tutorial provides a gentle introduction to the particle Metropolis-Hastings (PMH) algorithm for parameter inference in nonlinear state-space models together with a software implementation in the statistical programming language R. We employ a step-by-step approach to develop an implementation of the PMH algorithm (and the particle filter within) together with the reader. This final implementation is also available as the package pmhtutorial in the CRAN repository. Throughout the tutorial, we provide some intuition as to how the algorithm operates and discuss some solutions to problems that might occur in practice. To illustrate the use of PMH, we consider parameter inference in a linear Gaussian state-space model with synthetic data and a nonlinear stochastic volatility model with real-world data.

Bayesian optimisation for fast approximate inference in state-space models with intractable likelihoods

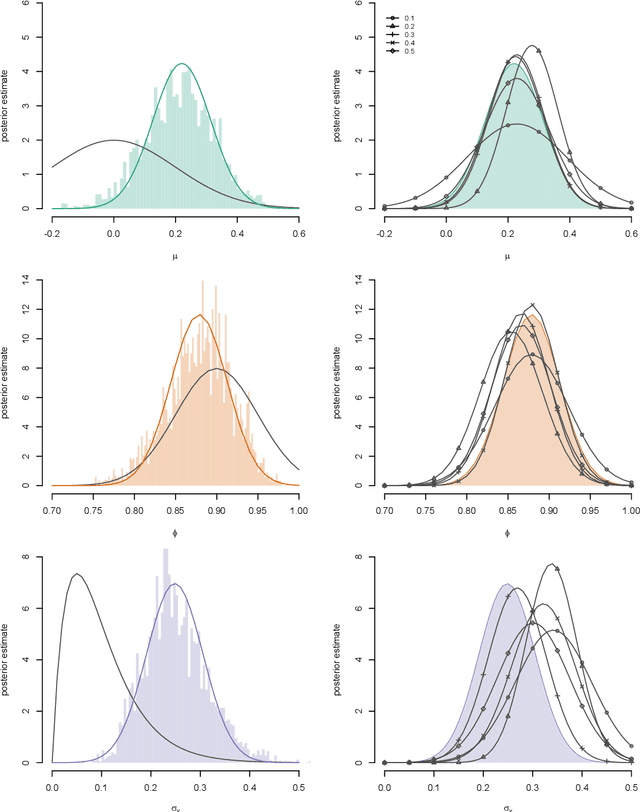
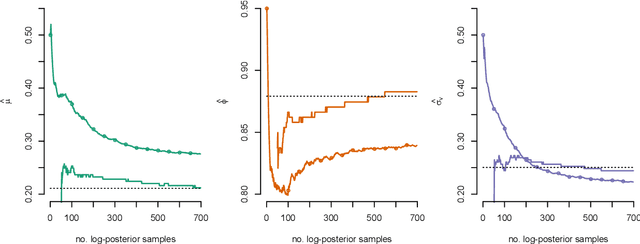
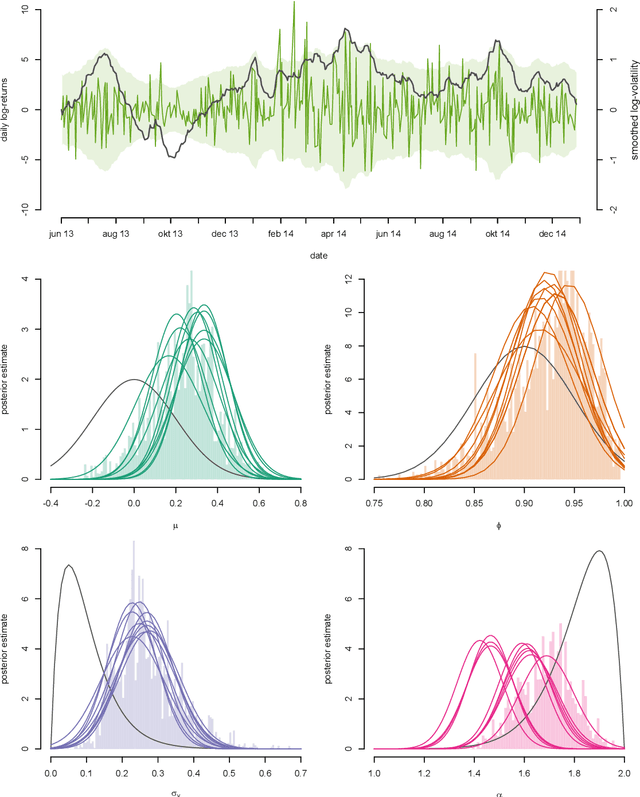
We consider the problem of approximate Bayesian parameter inference in non-linear state-space models with intractable likelihoods. Sequential Monte Carlo with approximate Bayesian computations (SMC-ABC) is one approach to approximate the likelihood in this type of models. However, such approximations can be noisy and computationally costly which hinders efficient implementations using standard methods based on optimisation and Monte Carlo methods. We propose a computationally efficient novel method based on the combination of Gaussian process optimisation and SMC-ABC to create a Laplace approximation of the intractable posterior. We exemplify the proposed algorithm for inference in stochastic volatility models with both synthetic and real-world data as well as for estimating the Value-at-Risk for two portfolios using a copula model. We document speed-ups of between one and two orders of magnitude compared to state-of-the-art algorithms for posterior inference.

Sequential Monte Carlo Methods for System Identification

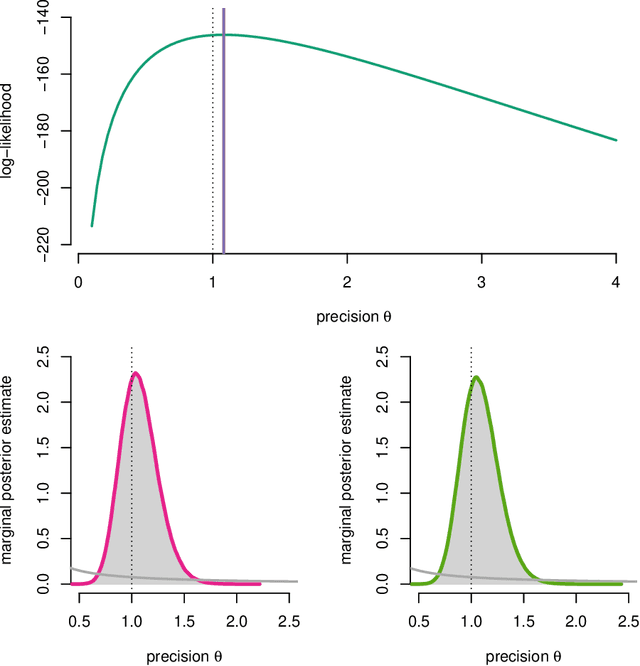
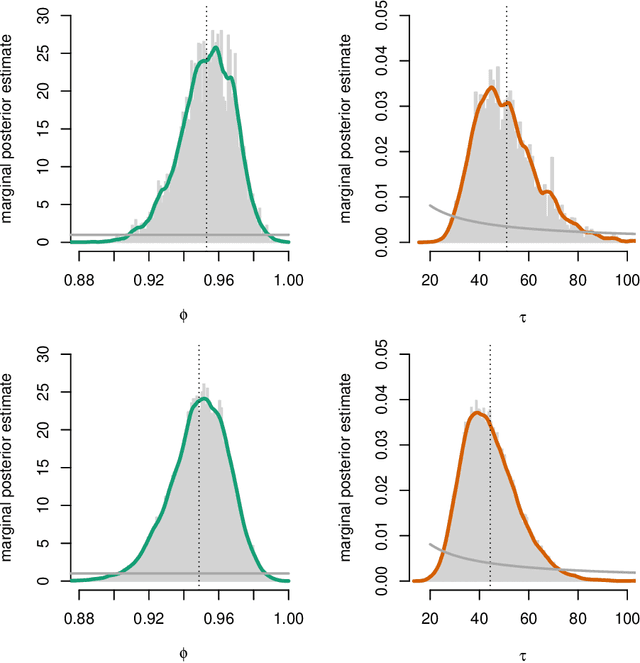
One of the key challenges in identifying nonlinear and possibly non-Gaussian state space models (SSMs) is the intractability of estimating the system state. Sequential Monte Carlo (SMC) methods, such as the particle filter (introduced more than two decades ago), provide numerical solutions to the nonlinear state estimation problems arising in SSMs. When combined with additional identification techniques, these algorithms provide solid solutions to the nonlinear system identification problem. We describe two general strategies for creating such combinations and discuss why SMC is a natural tool for implementing these strategies.

Accelerating pseudo-marginal Metropolis-Hastings by correlating auxiliary variables

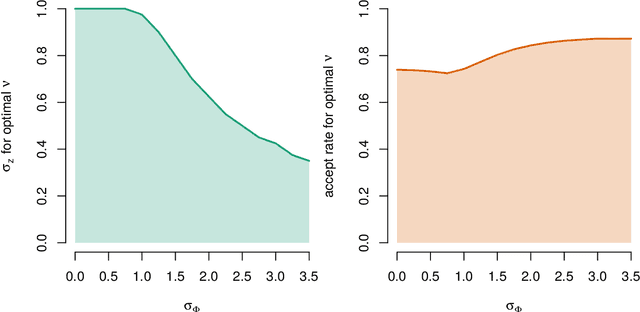
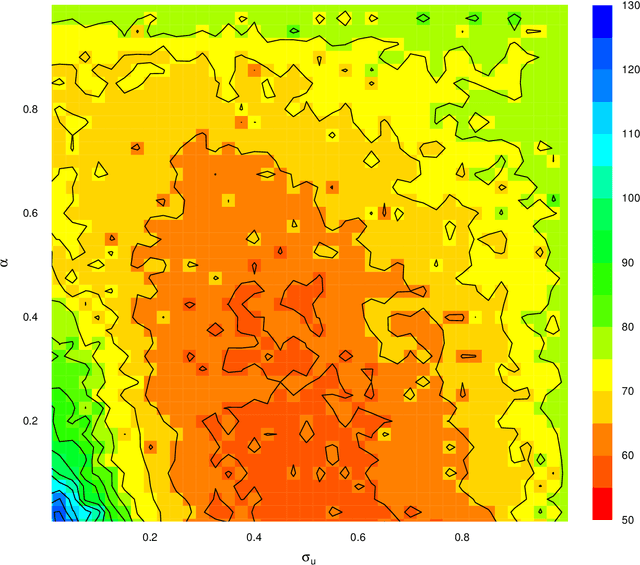
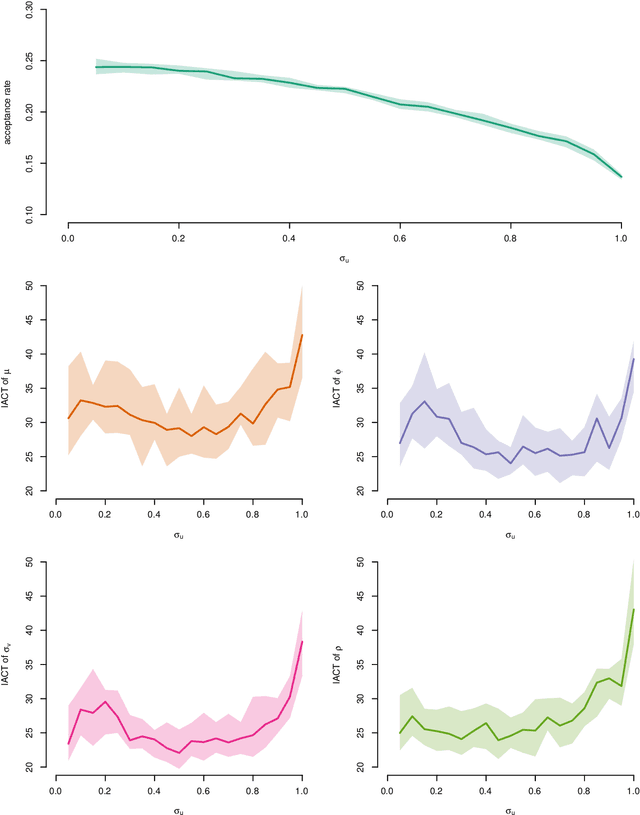
Pseudo-marginal Metropolis-Hastings (pmMH) is a powerful method for Bayesian inference in models where the posterior distribution is analytical intractable or computationally costly to evaluate directly. It operates by introducing additional auxiliary variables into the model and form an extended target distribution, which then can be evaluated point-wise. In many cases, the standard Metropolis-Hastings is then applied to sample from the extended target and the sought posterior can be obtained by marginalisation. However, in some implementations this approach suffers from poor mixing as the auxiliary variables are sampled from an independent proposal. We propose a modification to the pmMH algorithm in which a Crank-Nicolson (CN) proposal is used instead. This results in that we introduce a positive correlation in the auxiliary variables. We investigate how to tune the CN proposal and its impact on the mixing of the resulting pmMH sampler. The conclusion is that the proposed modification can have a beneficial effect on both the mixing of the Markov chain and the computational cost for each iteration of the pmMH algorithm.

Marginalizing Gaussian Process Hyperparameters using Sequential Monte Carlo

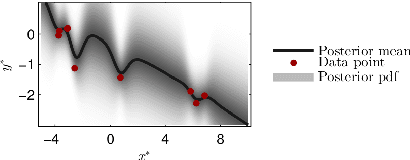
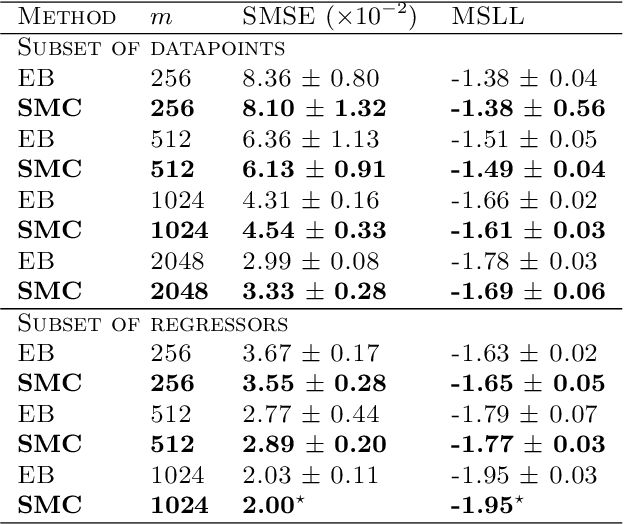
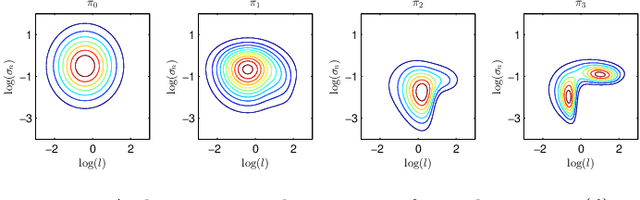
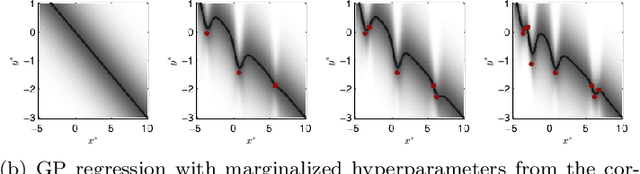
Gaussian process regression is a popular method for non-parametric probabilistic modeling of functions. The Gaussian process prior is characterized by so-called hyperparameters, which often have a large influence on the posterior model and can be difficult to tune. This work provides a method for numerical marginalization of the hyperparameters, relying on the rigorous framework of sequential Monte Carlo. Our method is well suited for online problems, and we demonstrate its ability to handle real-world problems with several dimensions and compare it to other marginalization methods. We also conclude that our proposed method is a competitive alternative to the commonly used point estimates maximizing the likelihood, both in terms of computational load and its ability to handle multimodal posteriors.

Newton-based maximum likelihood estimation in nonlinear state space models

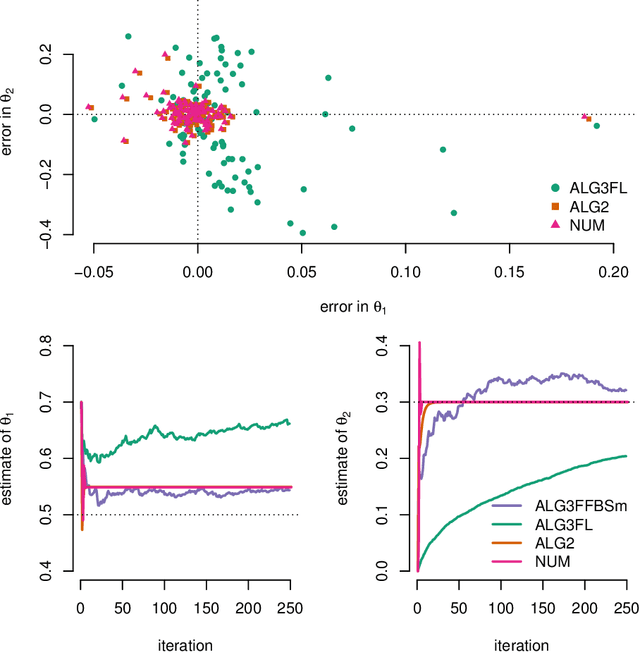
Maximum likelihood (ML) estimation using Newton's method in nonlinear state space models (SSMs) is a challenging problem due to the analytical intractability of the log-likelihood and its gradient and Hessian. We estimate the gradient and Hessian using Fisher's identity in combination with a smoothing algorithm. We explore two approximations of the log-likelihood and of the solution of the smoothing problem. The first is a linearization approximation which is computationally cheap, but the accuracy typically varies between models. The second is a sampling approximation which is asymptotically valid for any SSM but is more computationally costly. We demonstrate our approach for ML parameter estimation on simulated data from two different SSMs with encouraging results.

Quasi-Newton particle Metropolis-Hastings

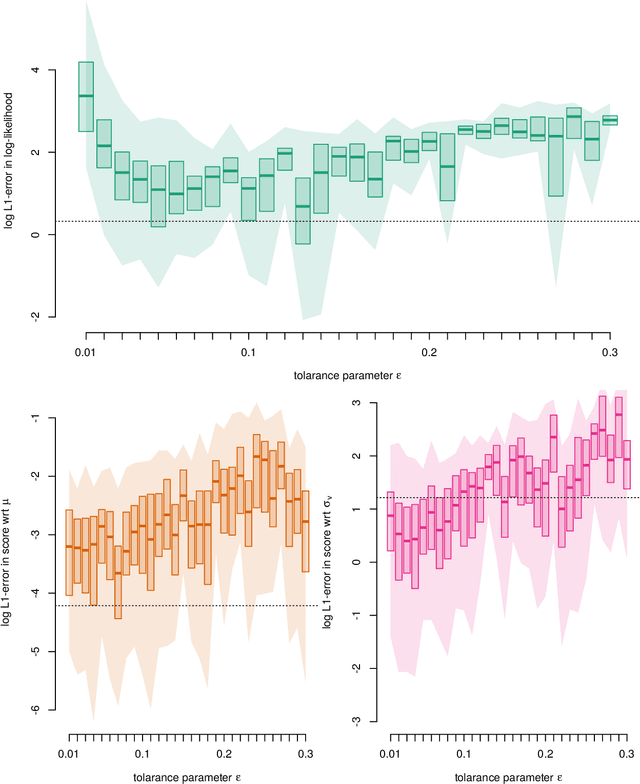
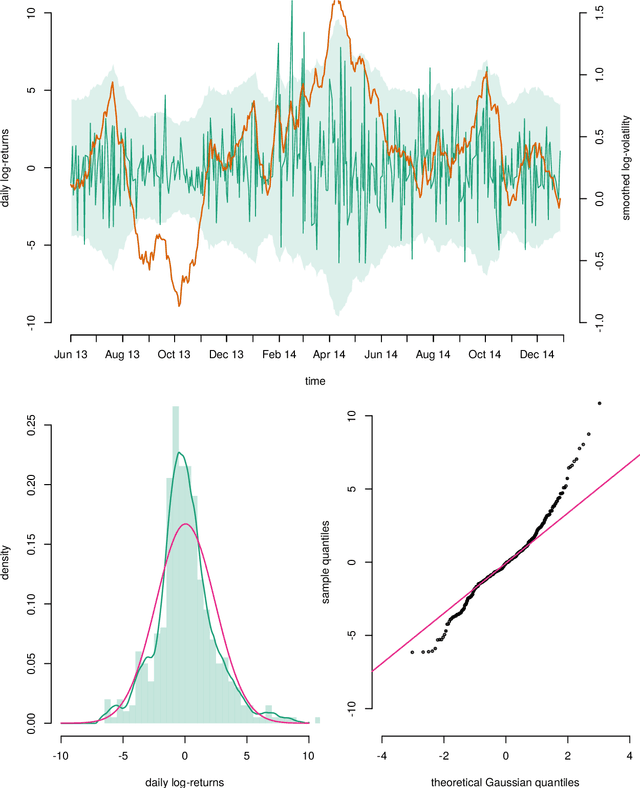
Particle Metropolis-Hastings enables Bayesian parameter inference in general nonlinear state space models (SSMs). However, in many implementations a random walk proposal is used and this can result in poor mixing if not tuned correctly using tedious pilot runs. Therefore, we consider a new proposal inspired by quasi-Newton algorithms that may achieve similar (or better) mixing with less tuning. An advantage compared to other Hessian based proposals, is that it only requires estimates of the gradient of the log-posterior. A possible application is parameter inference in the challenging class of SSMs with intractable likelihoods. We exemplify this application and the benefits of the new proposal by modelling log-returns of future contracts on coffee by a stochastic volatility model with $\alpha$-stable observations.

Particle Metropolis-Hastings using gradient and Hessian information

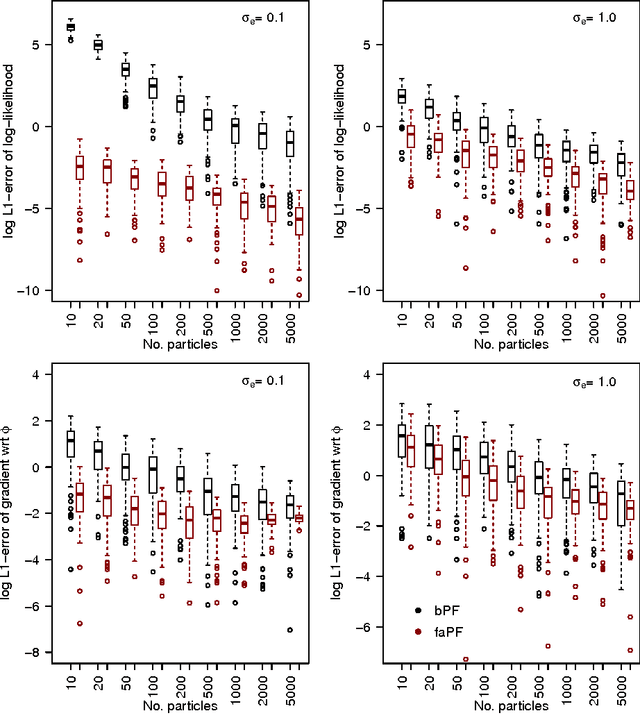
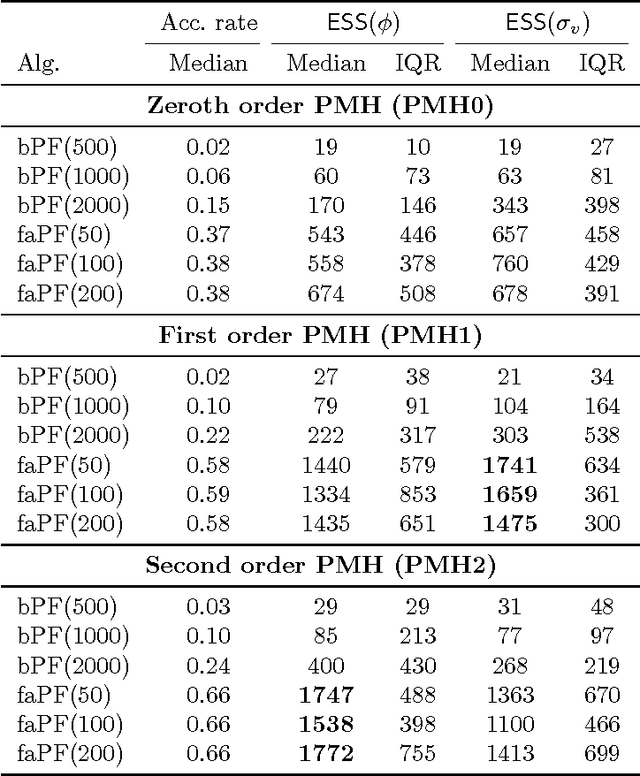
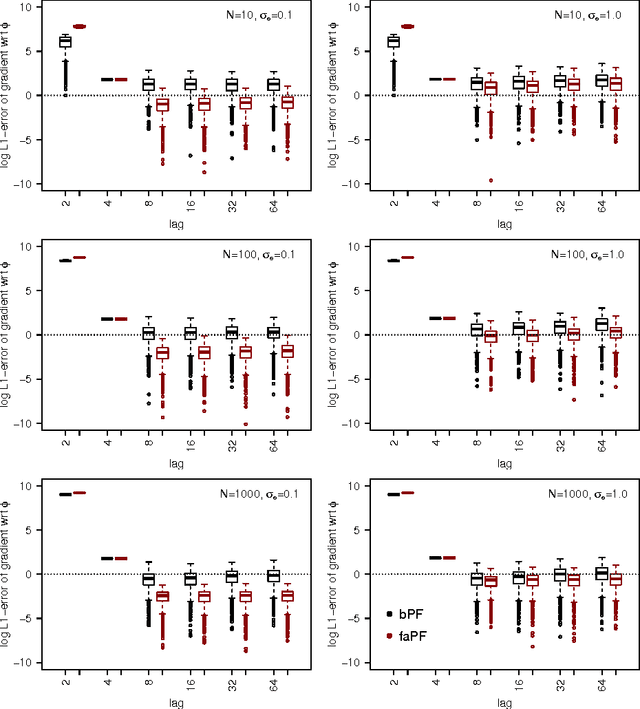
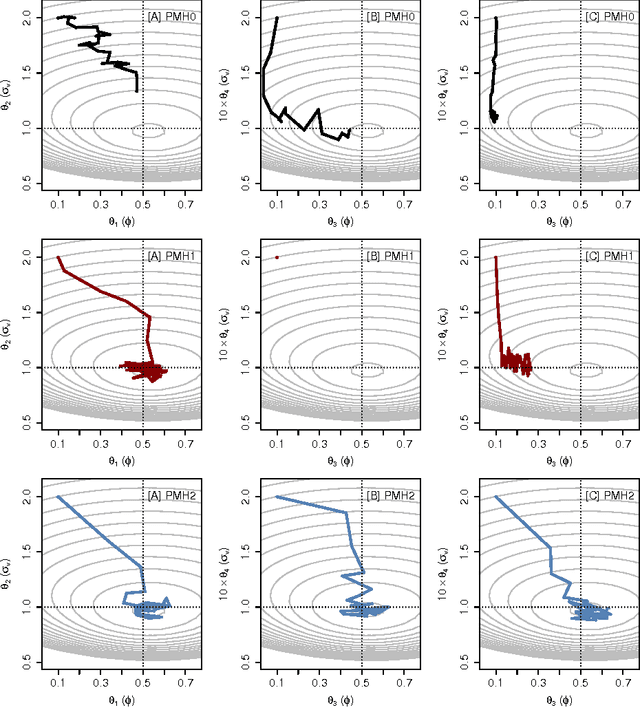
Particle Metropolis-Hastings (PMH) allows for Bayesian parameter inference in nonlinear state space models by combining Markov chain Monte Carlo (MCMC) and particle filtering. The latter is used to estimate the intractable likelihood. In its original formulation, PMH makes use of a marginal MCMC proposal for the parameters, typically a Gaussian random walk. However, this can lead to a poor exploration of the parameter space and an inefficient use of the generated particles. We propose a number of alternative versions of PMH that incorporate gradient and Hessian information about the posterior into the proposal. This information is more or less obtained as a byproduct of the likelihood estimation. Indeed, we show how to estimate the required information using a fixed-lag particle smoother, with a computational cost growing linearly in the number of particles. We conclude that the proposed methods can: (i) decrease the length of the burn-in phase, (ii) increase the mixing of the Markov chain at the stationary phase, and (iii) make the proposal distribution scale invariant which simplifies tuning.