Accelerating pseudo-marginal Metropolis-Hastings by correlating auxiliary variables
Paper and Code
Nov 17, 2015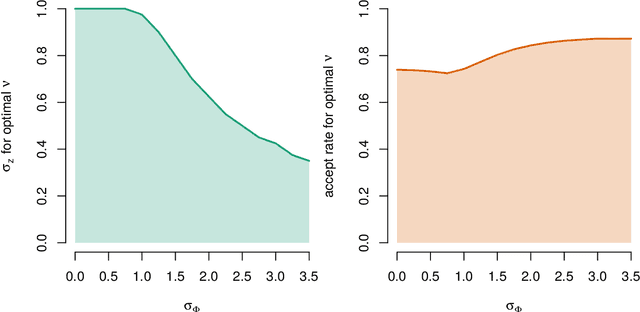

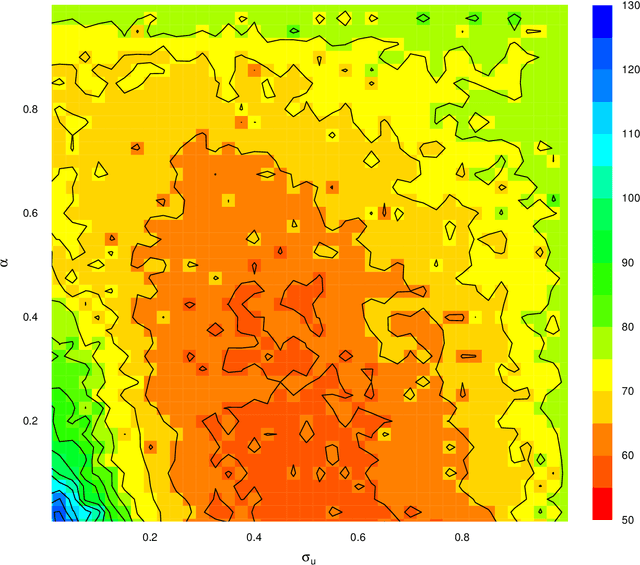
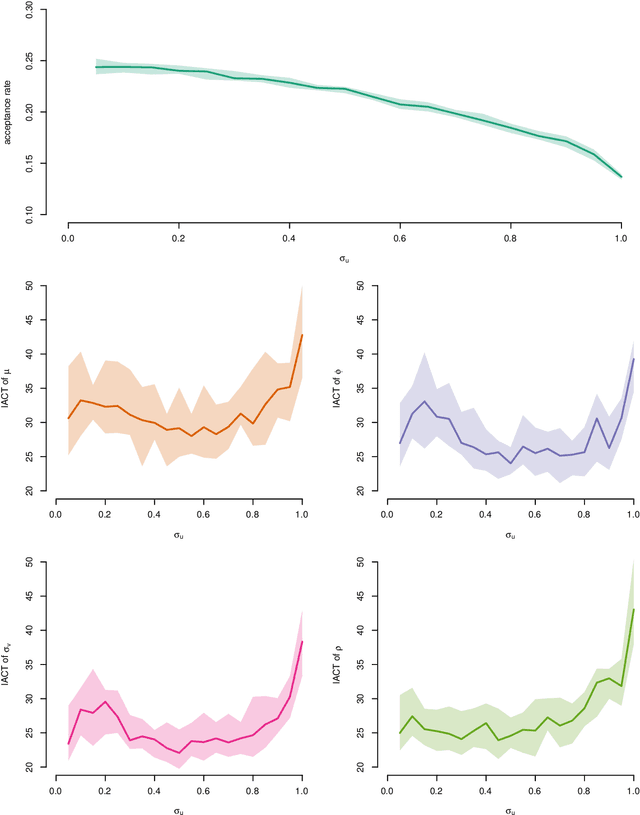
Pseudo-marginal Metropolis-Hastings (pmMH) is a powerful method for Bayesian inference in models where the posterior distribution is analytical intractable or computationally costly to evaluate directly. It operates by introducing additional auxiliary variables into the model and form an extended target distribution, which then can be evaluated point-wise. In many cases, the standard Metropolis-Hastings is then applied to sample from the extended target and the sought posterior can be obtained by marginalisation. However, in some implementations this approach suffers from poor mixing as the auxiliary variables are sampled from an independent proposal. We propose a modification to the pmMH algorithm in which a Crank-Nicolson (CN) proposal is used instead. This results in that we introduce a positive correlation in the auxiliary variables. We investigate how to tune the CN proposal and its impact on the mixing of the resulting pmMH sampler. The conclusion is that the proposed modification can have a beneficial effect on both the mixing of the Markov chain and the computational cost for each iteration of the pmMH algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge