A Bayesian Dynamic Multilayered Block Network Model

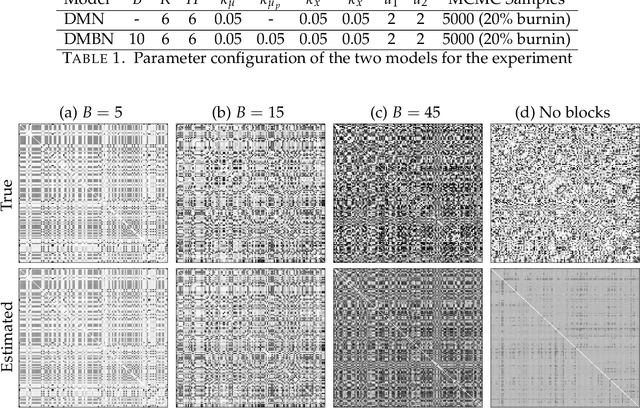
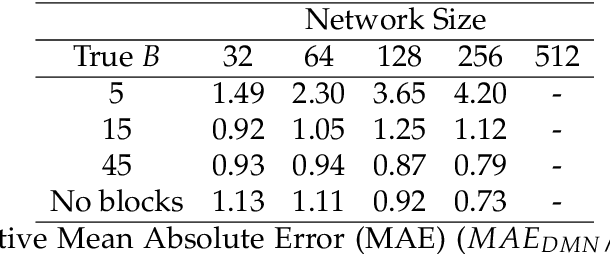
As network data become increasingly available, new opportunities arise to understand dynamic and multilayer network systems in many applied disciplines. Statistical modeling for multilayer networks is currently an active research area that aims to develop methods to carry out inference on such data. Recent contributions focus on latent space representation of the multilayer structure with underlying stochastic processes to account for network dynamics. Existing multilayer models are however typically limited to rather small networks. In this paper we introduce a dynamic multilayer block network model with a latent space represention for blocks rather than nodes. A block structure is natural for many real networks, such as social or transportation networks, where community structure naturally arises. A Gibbs sampler based on P\'olya-Gamma data augmentation is presented for the proposed model. Results from extensive simulations on synthetic data show that the inference algorithm scales well with the size of the network. We present a case study using real data from an airline system, a classic example of hub-and-spoke network.

Real-Time Robotic Search using Hierarchical Spatial Point Processes

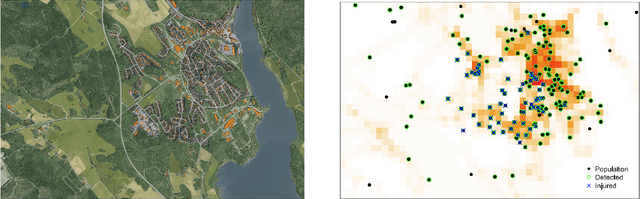
Aerial robots hold great potential for aiding Search and Rescue (SAR) efforts over large areas. Traditional approaches typically searches an area exhaustively, thereby ignoring that the density of victims varies based on predictable factors, such as the terrain, population density and the type of disaster. We present a probabilistic model to automate SAR planning, with explicit minimization of the expected time to discovery. The proposed model is a hierarchical spatial point process with three interacting spatial fields for i) the point patterns of persons in the area, ii) the probability of detecting persons and iii) the probability of injury. This structure allows inclusion of informative priors from e.g. geographic or cell phone traffic data, while falling back to latent Gaussian processes when priors are missing or inaccurate. To solve this problem in real-time, we propose a combination of fast approximate inference using Integrated Nested Laplace Approximation (INLA), and a novel Monte Carlo tree search tailored to the problem. Experiments using data simulated from real world GIS maps show that the framework outperforms traditional search strategies, and finds up to ten times more injured in the crucial first hours.

Subsampling MCMC - An introduction for the survey statistician

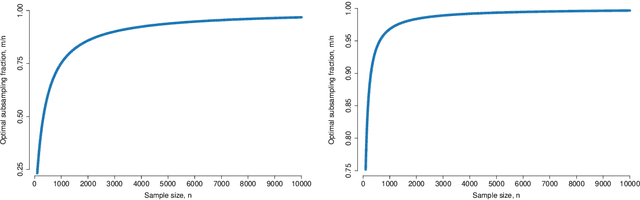
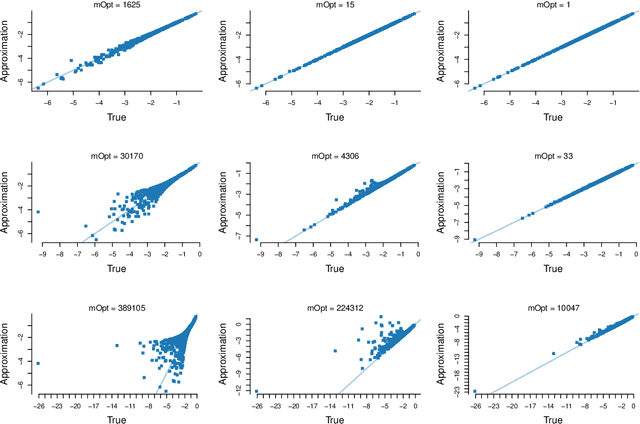
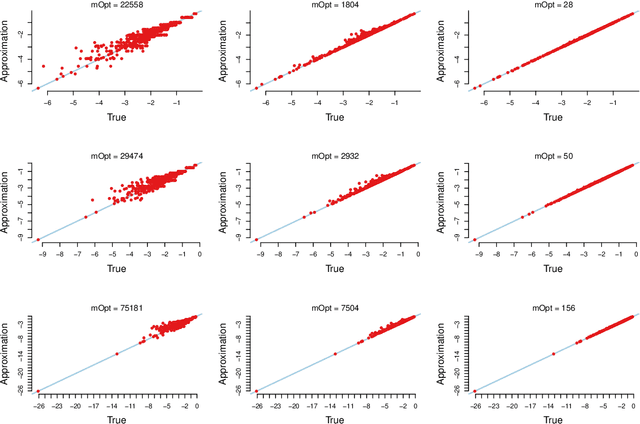
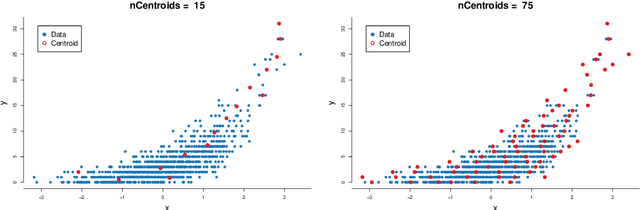
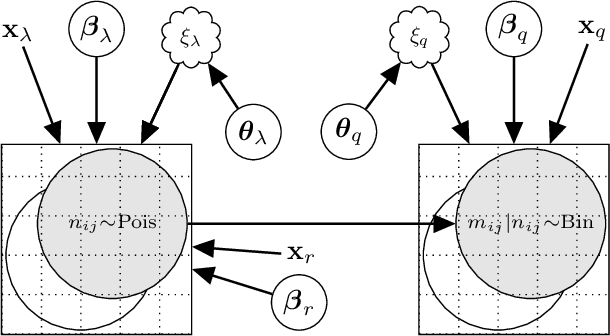
The rapid development of computing power and efficient Markov Chain Monte Carlo (MCMC) simulation algorithms have revolutionized Bayesian statistics, making it a highly practical inference method in applied work. However, MCMC algorithms tend to be computationally demanding, and are particularly slow for large datasets. Data subsampling has recently been suggested as a way to make MCMC methods scalable on massively large data, utilizing efficient sampling schemes and estimators from the survey sampling literature. These developments tend to be unknown by many survey statisticians who traditionally work with non-Bayesian methods, and rarely use MCMC. Our article explains the idea of data subsampling in MCMC by reviewing one strand of work, Subsampling MCMC, a so called pseudo-marginal MCMC approach to speeding up MCMC through data subsampling. The review is written for a survey statistician without previous knowledge of MCMC methods since our aim is to motivate survey sampling experts to contribute to the growing Subsampling MCMC literature.

The block-Poisson estimator for optimally tuned exact subsampling MCMC

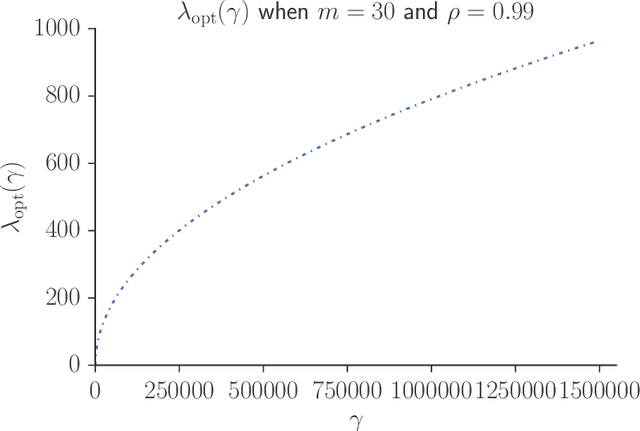
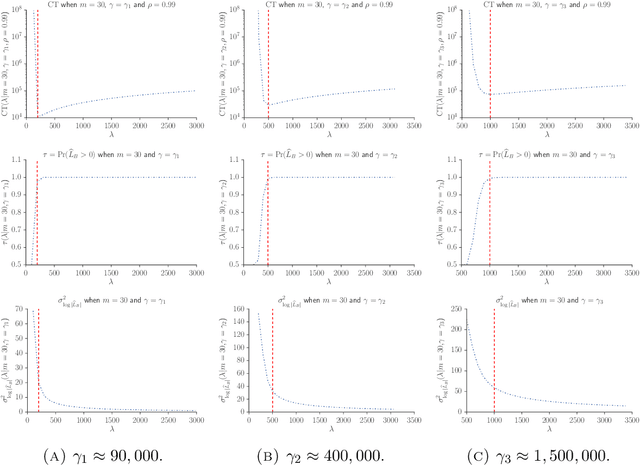
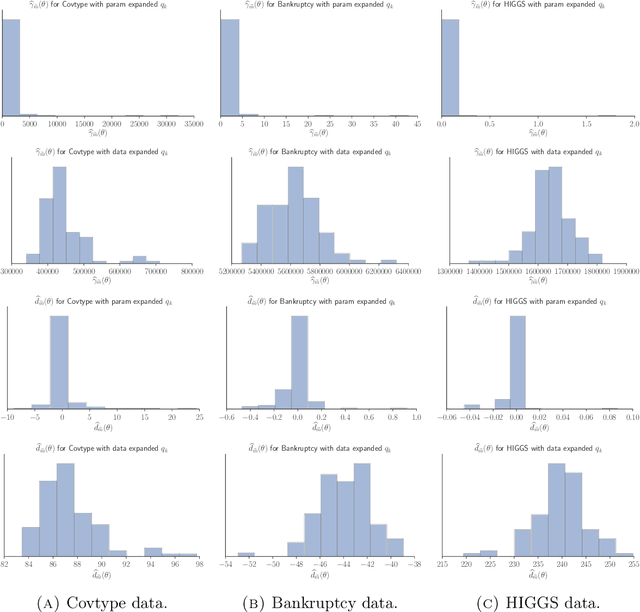
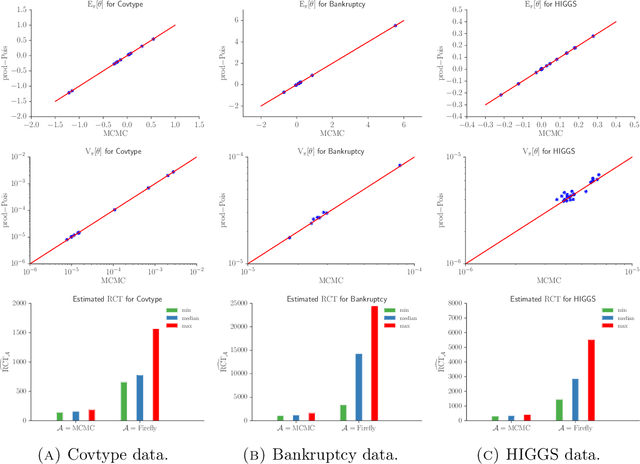
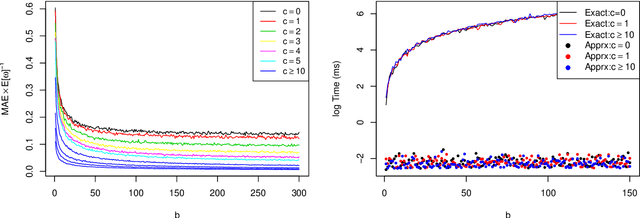
Speeding up Markov Chain Monte Carlo (MCMC) for datasets with many observations by data subsampling has recently received considerable attention in the literature. The currently available methods are either approximate, highly inefficient or limited to small dimensional models. We propose a pseudo-marginal MCMC method that estimates the likelihood by data subsampling using a block-Poisson estimator. The estimator is a product of Poisson estimators, each based on an independent subset of the observations. The construction allows us to update a subset of the blocks in each MCMC iteration, thereby inducing a controllable correlation between the estimates at the current and proposed draw in the Metropolis-Hastings ratio. This makes it possible to use highly variable likelihood estimators without adversely affecting the sampling efficiency. Poisson estimators are unbiased but not necessarily positive. We therefore follow Lyne et al. (2015) and run the MCMC on the absolute value of the estimator and use an importance sampling correction for occasionally negative likelihood estimates to estimate expectations of any function of the parameters. We provide analytically derived guidelines to select the optimal tuning parameters for the algorithm by minimizing the variance of the importance sampling corrected estimator per unit of computing time. The guidelines are derived under idealized conditions, but are demonstrated to be quite accurate in empirical experiments. The guidelines apply to any pseudo-marginal algorithm if the likelihood is estimated by the block-Poisson estimator, including the class of doubly intractable problems in Lyne et al. (2015). We illustrate the method in a logistic regression example and find dramatic improvements compared to regular MCMC without subsampling and a popular exact subsampling approach recently proposed in the literature.

Tree Ensembles with Rule Structured Horseshoe Regularization

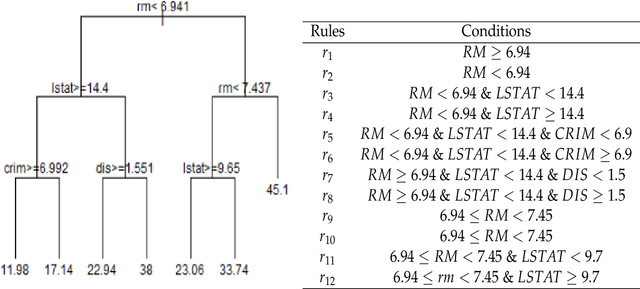
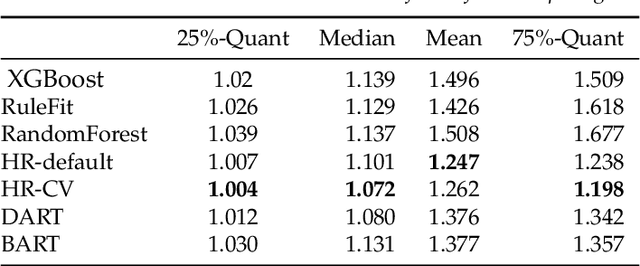
We propose a new Bayesian model for flexible nonlinear regression and classification using tree ensembles. The model is based on the RuleFit approach in Friedman and Popescu (2008) where rules from decision trees and linear terms are used in a L1-regularized regression. We modify RuleFit by replacing the L1-regularization by a horseshoe prior, which is well known to give aggressive shrinkage of noise predictor while leaving the important signal essentially untouched. This is especially important when a large number of rules are used as predictors as many of them only contribute noise. Our horseshoe prior has an additional hierarchical layer that applies more shrinkage a priori to rules with a large number of splits, and to rules that are only satisfied by a few observations. The aggressive noise shrinkage of our prior also makes it possible to complement the rules from boosting in Friedman and Popescu (2008) with an additional set of trees from random forest, which brings a desirable diversity to the ensemble. We sample from the posterior distribution using a very efficient and easily implemented Gibbs sampler. The new model is shown to outperform state-of-the-art methods like RuleFit, BART and random forest on 16 datasets. The model and its interpretation is demonstrated on the well known Boston housing data, and on gene expression data for cancer classification. The posterior sampling, prediction and graphical tools for interpreting the model results are implemented in a publicly available R package.

Speeding Up MCMC by Efficient Data Subsampling

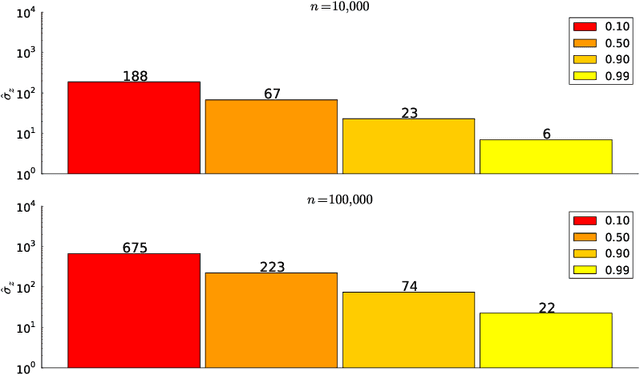
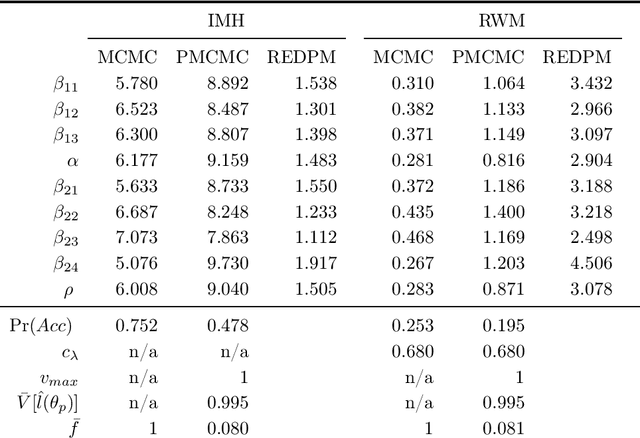
We propose Subsampling MCMC, a Markov Chain Monte Carlo (MCMC) framework where the likelihood function for $n$ observations is estimated from a random subset of $m$ observations. We introduce a highly efficient unbiased estimator of the log-likelihood based on control variates, such that the computing cost is much smaller than that of the full log-likelihood in standard MCMC. The likelihood estimate is bias-corrected and used in two dependent pseudo-marginal algorithms to sample from a perturbed posterior, for which we derive the asymptotic error with respect to $n$ and $m$, respectively. We propose a practical estimator of the error and show that the error is negligible even for a very small $m$ in our applications. We demonstrate that Subsampling MCMC is substantially more efficient than standard MCMC in terms of sampling efficiency for a given computational budget, and that it outperforms other subsampling methods for MCMC proposed in the literature.

Sparse Partially Collapsed MCMC for Parallel Inference in Topic Models

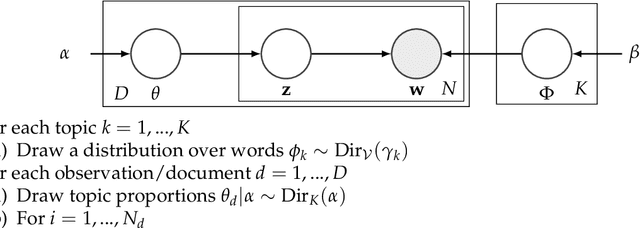
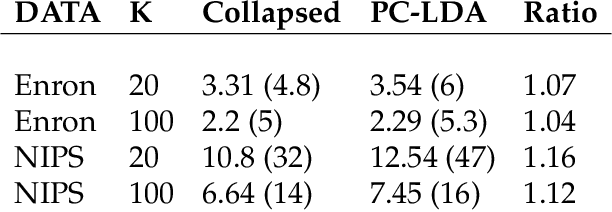
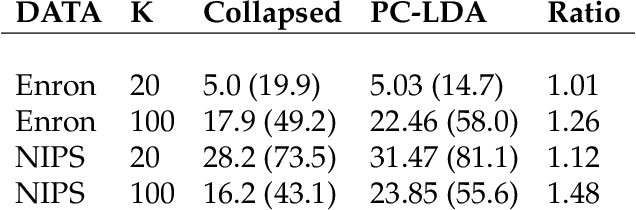
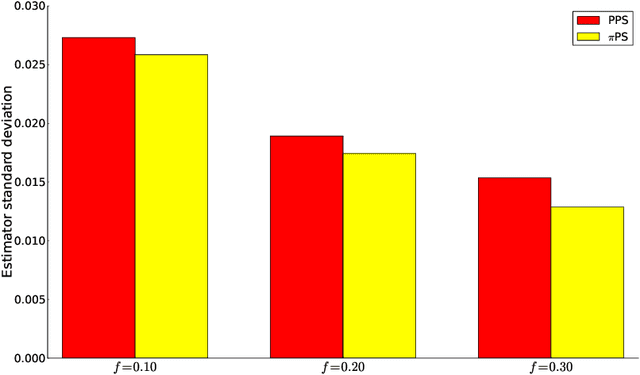
Topic models, and more specifically the class of Latent Dirichlet Allocation (LDA), are widely used for probabilistic modeling of text. MCMC sampling from the posterior distribution is typically performed using a collapsed Gibbs sampler. We propose a parallel sparse partially collapsed Gibbs sampler and compare its speed and efficiency to state-of-the-art samplers for topic models on five well-known text corpora of differing sizes and properties. In particular, we propose and compare two different strategies for sampling the parameter block with latent topic indicators. The experiments show that the increase in statistical inefficiency from only partial collapsing is smaller than commonly assumed, and can be more than compensated by the speedup from parallelization and sparsity on larger corpora. We also prove that the partially collapsed samplers scale well with the size of the corpus. The proposed algorithm is fast, efficient, exact, and can be used in more modeling situations than the ordinary collapsed sampler.

Hamiltonian Monte Carlo with Energy Conserving Subsampling

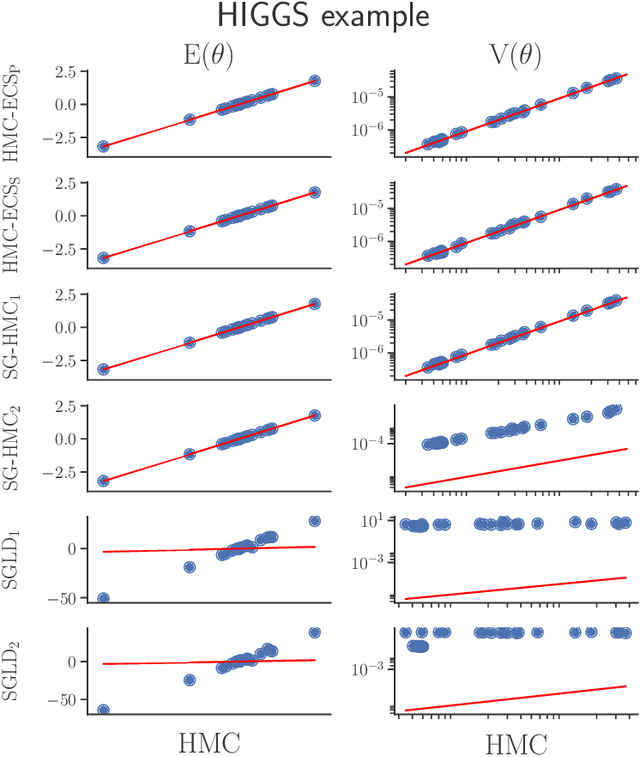
Hamiltonian Monte Carlo (HMC) has recently received considerable attention in the literature due to its ability to overcome the slow exploration of the parameter space inherent in random walk proposals. In tandem, data subsampling has been extensively used to overcome the computational bottlenecks in posterior sampling algorithms that require evaluating the likelihood over the whole data set, or its gradient. However, while data subsampling has been successful in traditional MCMC algorithms such as Metropolis-Hastings, it has been demonstrated to be unsuccessful in the context of HMC, both in terms of poor sampling efficiency and in producing highly biased inferences. We propose an efficient HMC-within-Gibbs algorithm that utilizes data subsampling to speed up computations and simulates from a slightly perturbed target, which is within $O(m^{-2})$ of the true target, where $m$ is the size of the subsample. We also show how to modify the method to obtain exact inference on any function of the parameters. Contrary to previous unsuccessful approaches, we perform subsampling in a way that conserves energy but for a modified Hamiltonian. We can therefore maintain high acceptance rates even for distant proposals. We apply the method for simulating from the posterior distribution of a high-dimensional spline model for bankruptcy data and document speed ups of several orders of magnitude compare to standard HMC and, moreover, demonstrate a negligible bias.

Scalable MCMC for Large Data Problems using Data Subsampling and the Difference Estimator

We propose a generic Markov Chain Monte Carlo (MCMC) algorithm to speed up computations for datasets with many observations. A key feature of our approach is the use of the highly efficient difference estimator from the survey sampling literature to estimate the log-likelihood accurately using only a small fraction of the data. Our algorithm improves on the $O(n)$ complexity of regular MCMC by operating over local data clusters instead of the full sample when computing the likelihood. The likelihood estimate is used in a Pseudo-marginal framework to sample from a perturbed posterior which is within $O(m^{-1/2})$ of the true posterior, where $m$ is the subsample size. The method is applied to a logistic regression model to predict firm bankruptcy for a large data set. We document a significant speed up in comparison to the standard MCMC on the full dataset.

Bayesian optimisation for fast approximate inference in state-space models with intractable likelihoods

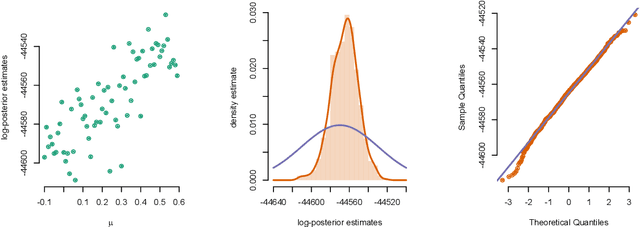
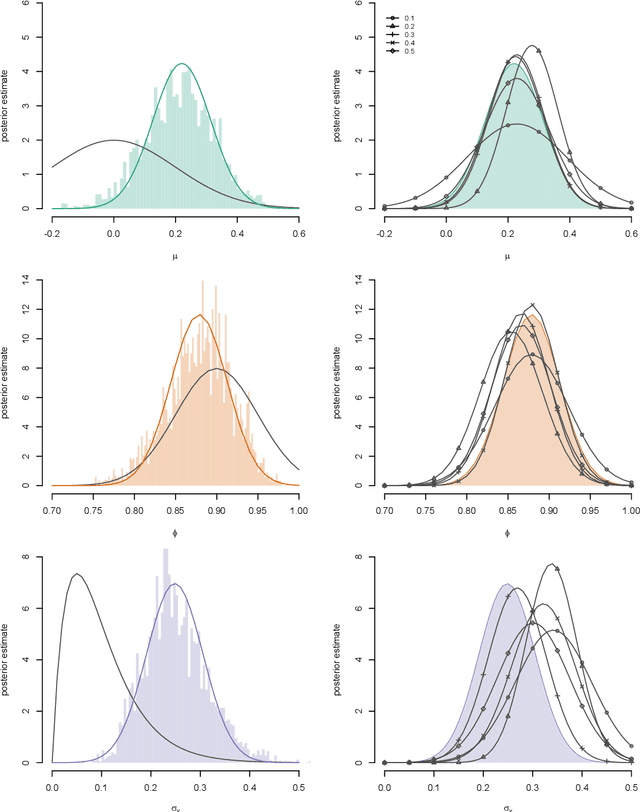
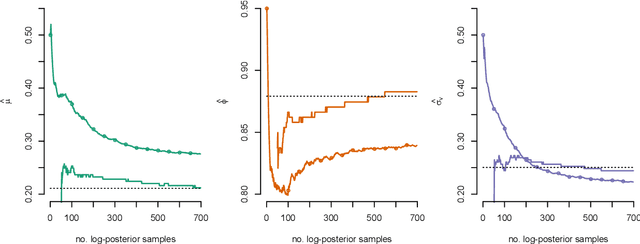
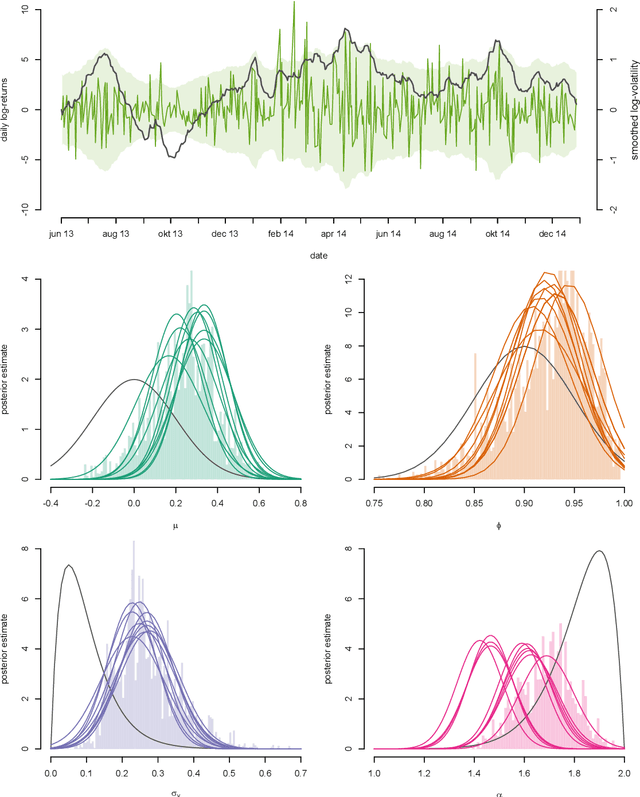
We consider the problem of approximate Bayesian parameter inference in non-linear state-space models with intractable likelihoods. Sequential Monte Carlo with approximate Bayesian computations (SMC-ABC) is one approach to approximate the likelihood in this type of models. However, such approximations can be noisy and computationally costly which hinders efficient implementations using standard methods based on optimisation and Monte Carlo methods. We propose a computationally efficient novel method based on the combination of Gaussian process optimisation and SMC-ABC to create a Laplace approximation of the intractable posterior. We exemplify the proposed algorithm for inference in stochastic volatility models with both synthetic and real-world data as well as for estimating the Value-at-Risk for two portfolios using a copula model. We document speed-ups of between one and two orders of magnitude compared to state-of-the-art algorithms for posterior inference.