Comparing Machine Learning Algorithms by Union-Free Generic Depth

We propose a framework for descriptively analyzing sets of partial orders based on the concept of depth functions. Despite intensive studies in linear and metric spaces, there is very little discussion on depth functions for non-standard data types such as partial orders. We introduce an adaptation of the well-known simplicial depth to the set of all partial orders, the union-free generic (ufg) depth. Moreover, we utilize our ufg depth for a comparison of machine learning algorithms based on multidimensional performance measures. Concretely, we provide two examples of classifier comparisons on samples of standard benchmark data sets. Our results demonstrate promisingly the wide variety of different analysis approaches based on ufg methods. Furthermore, the examples outline that our approach differs substantially from existing benchmarking approaches, and thus adds a new perspective to the vivid debate on classifier comparison.

Evaluating machine learning models in non-standard settings: An overview and new findings

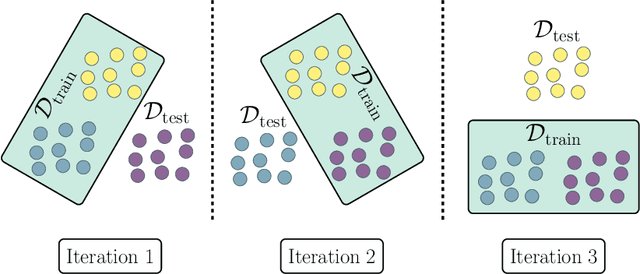
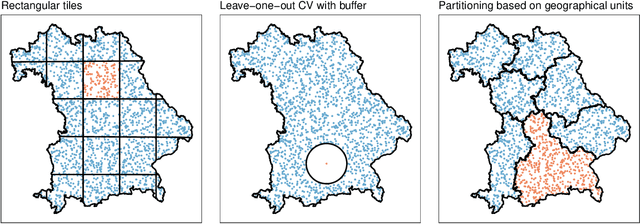
Estimating the generalization error (GE) of machine learning models is fundamental, with resampling methods being the most common approach. However, in non-standard settings, particularly those where observations are not independently and identically distributed, resampling using simple random data divisions may lead to biased GE estimates. This paper strives to present well-grounded guidelines for GE estimation in various such non-standard settings: clustered data, spatial data, unequal sampling probabilities, concept drift, and hierarchically structured outcomes. Our overview combines well-established methodologies with other existing methods that, to our knowledge, have not been frequently considered in these particular settings. A unifying principle among these techniques is that the test data used in each iteration of the resampling procedure should reflect the new observations to which the model will be applied, while the training data should be representative of the entire data set used to obtain the final model. Beyond providing an overview, we address literature gaps by conducting simulation studies. These studies assess the necessity of using GE-estimation methods tailored to the respective setting. Our findings corroborate the concern that standard resampling methods often yield biased GE estimates in non-standard settings, underscoring the importance of tailored GE estimation.

Depth Functions for Partial Orders with a Descriptive Analysis of Machine Learning Algorithms

We propose a framework for descriptively analyzing sets of partial orders based on the concept of depth functions. Despite intensive studies of depth functions in linear and metric spaces, there is very little discussion on depth functions for non-standard data types such as partial orders. We introduce an adaptation of the well-known simplicial depth to the set of all partial orders, the union-free generic (ufg) depth. Moreover, we utilize our ufg depth for a comparison of machine learning algorithms based on multidimensional performance measures. Concretely, we analyze the distribution of different classifier performances over a sample of standard benchmark data sets. Our results promisingly demonstrate that our approach differs substantially from existing benchmarking approaches and, therefore, adds a new perspective to the vivid debate on the comparison of classifiers.

Statistical Comparisons of Classifiers by Generalized Stochastic Dominance

Although being a question in the very methodological core of machine learning, there is still no unanimous consensus on how to compare classifiers. Every comparison framework is confronted with (at least) three fundamental challenges: the multiplicity of quality criteria, the multiplicity of data sets and the randomness/arbitrariness of the selection of data sets. In this paper, we add a fresh view to the vivid debate by adopting recent developments in decision theory. Our resulting framework, based on so-called preference systems, ranks classifiers by a generalized concept of stochastic dominance, which powerfully circumvents the cumbersome, and often even self-contradictory, reliance on aggregates. Moreover, we show that generalized stochastic dominance can be operationalized by solving easy-to-handle linear programs and statistically tested by means of an adapted two-sample observation-randomization test. This indeed yields a powerful framework for the statistical comparison of classifiers with respect to multiple quality criteria simultaneously. We illustrate and investigate our framework in a simulation study and with standard benchmark data sets.

Tree Ensembles with Rule Structured Horseshoe Regularization

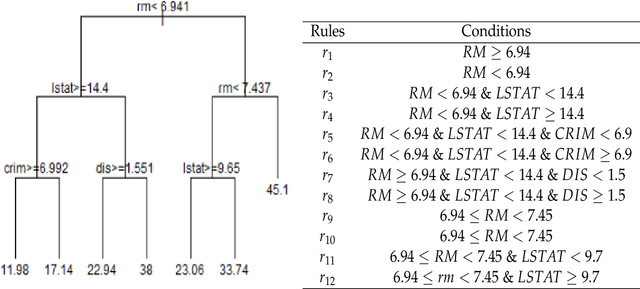
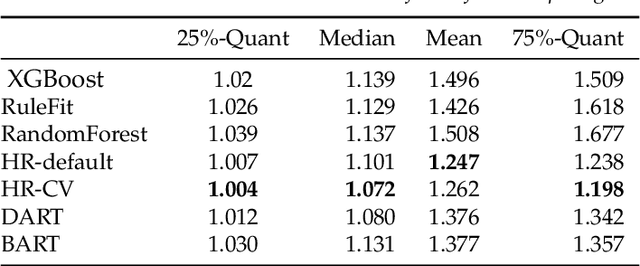
We propose a new Bayesian model for flexible nonlinear regression and classification using tree ensembles. The model is based on the RuleFit approach in Friedman and Popescu (2008) where rules from decision trees and linear terms are used in a L1-regularized regression. We modify RuleFit by replacing the L1-regularization by a horseshoe prior, which is well known to give aggressive shrinkage of noise predictor while leaving the important signal essentially untouched. This is especially important when a large number of rules are used as predictors as many of them only contribute noise. Our horseshoe prior has an additional hierarchical layer that applies more shrinkage a priori to rules with a large number of splits, and to rules that are only satisfied by a few observations. The aggressive noise shrinkage of our prior also makes it possible to complement the rules from boosting in Friedman and Popescu (2008) with an additional set of trees from random forest, which brings a desirable diversity to the ensemble. We sample from the posterior distribution using a very efficient and easily implemented Gibbs sampler. The new model is shown to outperform state-of-the-art methods like RuleFit, BART and random forest on 16 datasets. The model and its interpretation is demonstrated on the well known Boston housing data, and on gene expression data for cancer classification. The posterior sampling, prediction and graphical tools for interpreting the model results are implemented in a publicly available R package.