Thomas Augustin
Ludwig-Maximilians-Universität München
Consensus in Motion: A Case of Dynamic Rationality of Sequential Learning in Probability Aggregation
Apr 20, 2025Abstract:We propose a framework for probability aggregation based on propositional probability logic. Unlike conventional judgment aggregation, which focuses on static rationality, our model addresses dynamic rationality by ensuring that collective beliefs update consistently with new information. We show that any consensus-compatible and independent aggregation rule on a non-nested agenda is necessarily linear. Furthermore, we provide sufficient conditions for a fair learning process, where individuals initially agree on a specified subset of propositions known as the common ground, and new information is restricted to this shared foundation. This guarantees that updating individual judgments via Bayesian conditioning-whether performed before or after aggregation-yields the same collective belief. A distinctive feature of our framework is its treatment of sequential decision-making, which allows new information to be incorporated progressively through multiple stages while maintaining the established common ground. We illustrate our findings with a running example in a political scenario concerning healthcare and immigration policies.
A Statistical Case Against Empirical Human-AI Alignment
Feb 20, 2025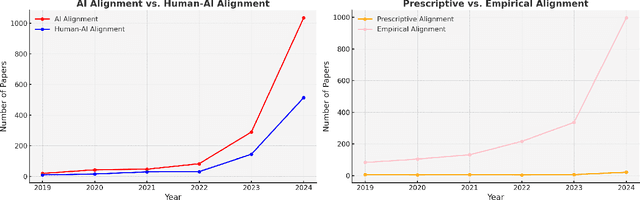



Abstract:Empirical human-AI alignment aims to make AI systems act in line with observed human behavior. While noble in its goals, we argue that empirical alignment can inadvertently introduce statistical biases that warrant caution. This position paper thus advocates against naive empirical alignment, offering prescriptive alignment and a posteriori empirical alignment as alternatives. We substantiate our principled argument by tangible examples like human-centric decoding of language models.
Statistical Multicriteria Benchmarking via the GSD-Front
Jun 06, 2024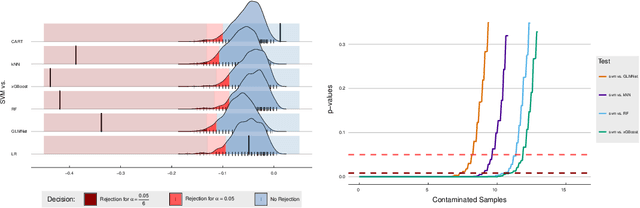
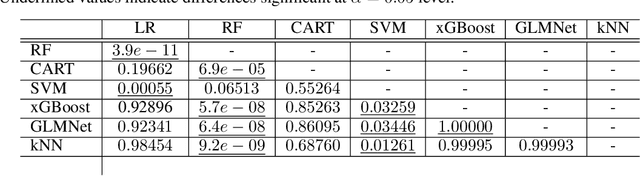
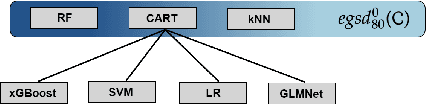
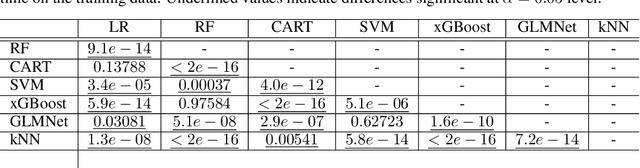
Abstract:Given the vast number of classifiers that have been (and continue to be) proposed, reliable methods for comparing them are becoming increasingly important. The desire for reliability is broken down into three main aspects: (1) Comparisons should allow for different quality metrics simultaneously. (2) Comparisons should take into account the statistical uncertainty induced by the choice of benchmark suite. (3) The robustness of the comparisons under small deviations in the underlying assumptions should be verifiable. To address (1), we propose to compare classifiers using a generalized stochastic dominance ordering (GSD) and present the GSD-front as an information-efficient alternative to the classical Pareto-front. For (2), we propose a consistent statistical estimator for the GSD-front and construct a statistical test for whether a (potentially new) classifier lies in the GSD-front of a set of state-of-the-art classifiers. For (3), we relax our proposed test using techniques from robust statistics and imprecise probabilities. We illustrate our concepts on the benchmark suite PMLB and on the platform OpenML.
Explaining Bayesian Optimization by Shapley Values Facilitates Human-AI Collaboration
Mar 08, 2024



Abstract:Bayesian optimization (BO) with Gaussian processes (GP) has become an indispensable algorithm for black box optimization problems. Not without a dash of irony, BO is often considered a black box itself, lacking ways to provide reasons as to why certain parameters are proposed to be evaluated. This is particularly relevant in human-in-the-loop applications of BO, such as in robotics. We address this issue by proposing ShapleyBO, a framework for interpreting BO's proposals by game-theoretic Shapley values.They quantify each parameter's contribution to BO's acquisition function. Exploiting the linearity of Shapley values, we are further able to identify how strongly each parameter drives BO's exploration and exploitation for additive acquisition functions like the confidence bound. We also show that ShapleyBO can disentangle the contributions to exploration into those that explore aleatoric and epistemic uncertainty. Moreover, our method gives rise to a ShapleyBO-assisted human machine interface (HMI), allowing users to interfere with BO in case proposals do not align with human reasoning. We demonstrate this HMI's benefits for the use case of personalizing wearable robotic devices (assistive back exosuits) by human-in-the-loop BO. Results suggest human-BO teams with access to ShapleyBO can achieve lower regret than teams without.
Evaluating machine learning models in non-standard settings: An overview and new findings
Oct 23, 2023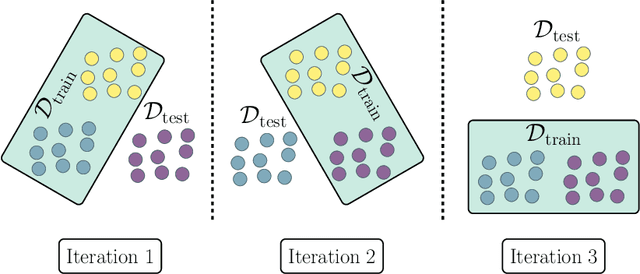

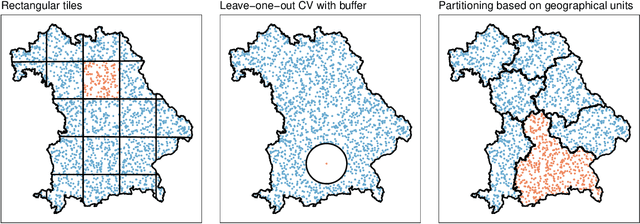

Abstract:Estimating the generalization error (GE) of machine learning models is fundamental, with resampling methods being the most common approach. However, in non-standard settings, particularly those where observations are not independently and identically distributed, resampling using simple random data divisions may lead to biased GE estimates. This paper strives to present well-grounded guidelines for GE estimation in various such non-standard settings: clustered data, spatial data, unequal sampling probabilities, concept drift, and hierarchically structured outcomes. Our overview combines well-established methodologies with other existing methods that, to our knowledge, have not been frequently considered in these particular settings. A unifying principle among these techniques is that the test data used in each iteration of the resampling procedure should reflect the new observations to which the model will be applied, while the training data should be representative of the entire data set used to obtain the final model. Beyond providing an overview, we address literature gaps by conducting simulation studies. These studies assess the necessity of using GE-estimation methods tailored to the respective setting. Our findings corroborate the concern that standard resampling methods often yield biased GE estimates in non-standard settings, underscoring the importance of tailored GE estimation.
Robust Statistical Comparison of Random Variables with Locally Varying Scale of Measurement
Jun 22, 2023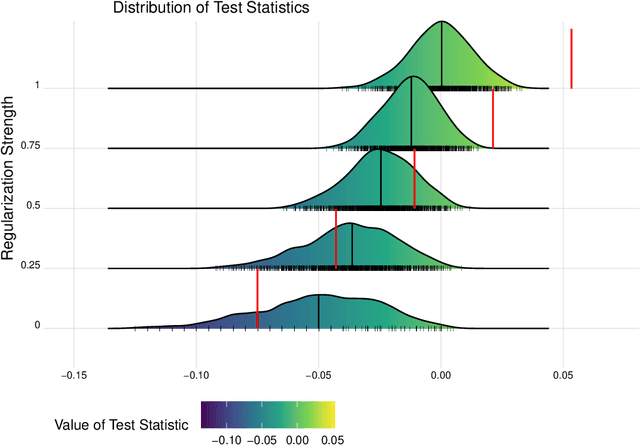
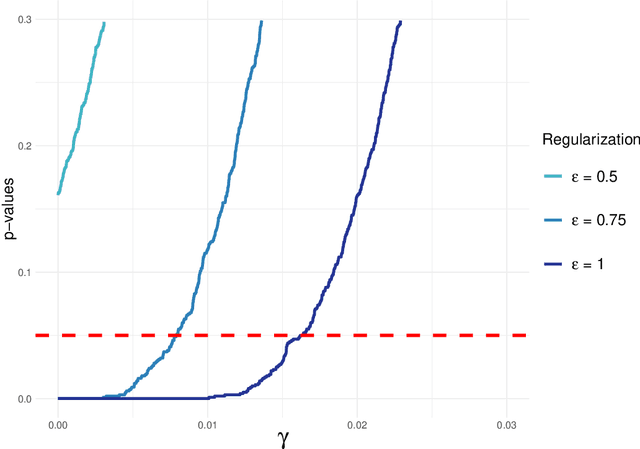
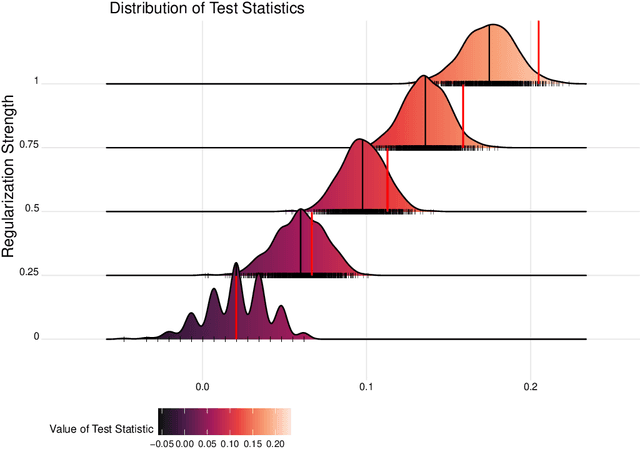
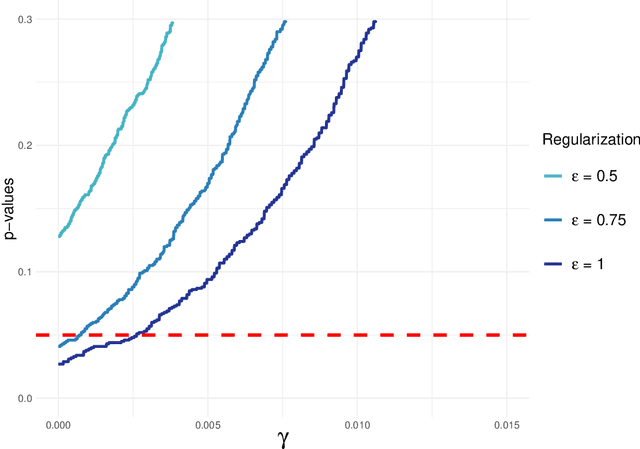
Abstract:Spaces with locally varying scale of measurement, like multidimensional structures with differently scaled dimensions, are pretty common in statistics and machine learning. Nevertheless, it is still understood as an open question how to exploit the entire information encoded in them properly. We address this problem by considering an order based on (sets of) expectations of random variables mapping into such non-standard spaces. This order contains stochastic dominance and expectation order as extreme cases when no, or respectively perfect, cardinal structure is given. We derive a (regularized) statistical test for our proposed generalized stochastic dominance (GSD) order, operationalize it by linear optimization, and robustify it by imprecise probability models. Our findings are illustrated with data from multidimensional poverty measurement, finance, and medicine.
In all LikelihoodS: How to Reliably Select Pseudo-Labeled Data for Self-Training in Semi-Supervised Learning
Mar 02, 2023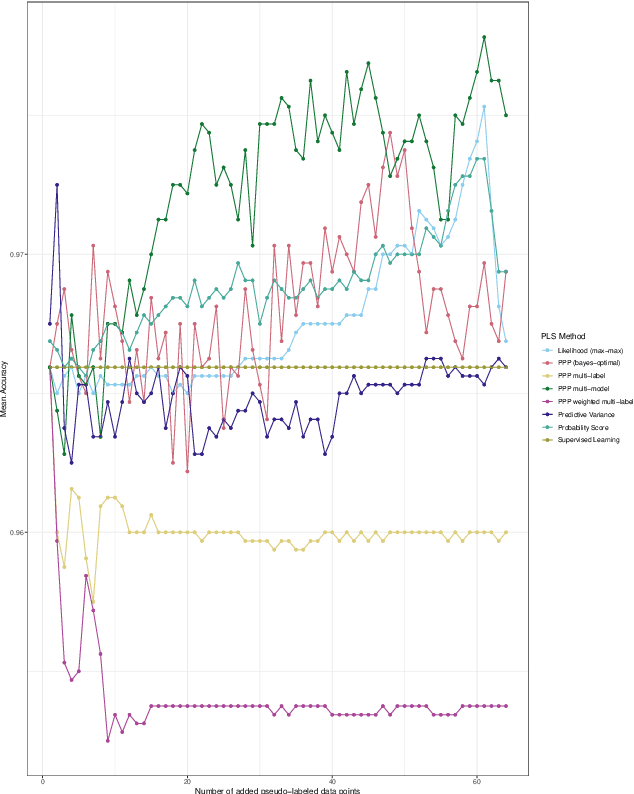
Abstract:Self-training is a simple yet effective method within semi-supervised learning. The idea is to iteratively enhance training data by adding pseudo-labeled data. Its generalization performance heavily depends on the selection of these pseudo-labeled data (PLS). In this paper, we aim at rendering PLS more robust towards the involved modeling assumptions. To this end, we propose to select pseudo-labeled data that maximize a multi-objective utility function. The latter is constructed to account for different sources of uncertainty, three of which we discuss in more detail: model selection, accumulation of errors and covariate shift. In the absence of second-order information on such uncertainties, we furthermore consider the generic approach of the generalized Bayesian alpha-cut updating rule for credal sets. As a practical proof of concept, we spotlight the application of three of our robust extensions on simulated and real-world data. Results suggest that in particular robustness w.r.t. model choice can lead to substantial accuracy gains.
Approximate Bayes Optimal Pseudo-Label Selection
Feb 20, 2023Abstract:Semi-supervised learning by self-training heavily relies on pseudo-label selection (PLS). The selection often depends on the initial model fit on labeled data. Early overfitting might thus be propagated to the final model by selecting instances with overconfident but erroneous predictions, often referred to as confirmation bias. This paper introduces BPLS, a Bayesian framework for PLS that aims to mitigate this issue. At its core lies a criterion for selecting instances to label: an analytical approximation of the posterior predictive of pseudo-samples. We derive this selection criterion by proving Bayes optimality of the posterior predictive of pseudo-samples. We further overcome computational hurdles by approximating the criterion analytically. Its relation to the marginal likelihood allows us to come up with an approximation based on Laplace's method and the Gaussian integral. We empirically assess BPLS for parametric generalized linear and non-parametric generalized additive models on simulated and real-world data. When faced with high-dimensional data prone to overfitting, BPLS outperforms traditional PLS methods.
Multi-Target Decision Making under Conditions of Severe Uncertainty
Dec 13, 2022


Abstract:The quality of consequences in a decision making problem under (severe) uncertainty must often be compared among different targets (goals, objectives) simultaneously. In addition, the evaluations of a consequence's performance under the various targets often differ in their scale of measurement, classically being either purely ordinal or perfectly cardinal. In this paper, we transfer recent developments from abstract decision theory with incomplete preferential and probabilistic information to this multi-target setting and show how -- by exploiting the (potentially) partial cardinal and partial probabilistic information -- more informative orders for comparing decisions can be given than the Pareto order. We discuss some interesting properties of the proposed orders between decision options and show how they can be concretely computed by linear optimization. We conclude the paper by demonstrating our framework in an artificial (but quite real-world) example in the context of comparing algorithms under different performance measures.
Statistical Comparisons of Classifiers by Generalized Stochastic Dominance
Sep 05, 2022



Abstract:Although being a question in the very methodological core of machine learning, there is still no unanimous consensus on how to compare classifiers. Every comparison framework is confronted with (at least) three fundamental challenges: the multiplicity of quality criteria, the multiplicity of data sets and the randomness/arbitrariness of the selection of data sets. In this paper, we add a fresh view to the vivid debate by adopting recent developments in decision theory. Our resulting framework, based on so-called preference systems, ranks classifiers by a generalized concept of stochastic dominance, which powerfully circumvents the cumbersome, and often even self-contradictory, reliance on aggregates. Moreover, we show that generalized stochastic dominance can be operationalized by solving easy-to-handle linear programs and statistically tested by means of an adapted two-sample observation-randomization test. This indeed yields a powerful framework for the statistical comparison of classifiers with respect to multiple quality criteria simultaneously. We illustrate and investigate our framework in a simulation study and with standard benchmark data sets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge