Towards Better Open-Ended Text Generation: A Multicriteria Evaluation Framework

Open-ended text generation has become a prominent task in natural language processing due to the rise of powerful (large) language models. However, evaluating the quality of these models and the employed decoding strategies remains challenging because of trade-offs among widely used metrics such as coherence, diversity, and perplexity. Decoding methods often excel in some metrics while underperforming in others, complicating the establishment of a clear ranking. In this paper, we present novel ranking strategies within this multicriteria framework. Specifically, we employ benchmarking approaches based on partial orderings and present a new summary metric designed to balance existing automatic indicators, providing a more holistic evaluation of text generation quality. Furthermore, we discuss the alignment of these approaches with human judgments. Our experiments demonstrate that the proposed methods offer a robust way to compare decoding strategies, exhibit similarities with human preferences, and serve as valuable tools in guiding model selection for open-ended text generation tasks. Finally, we suggest future directions for improving evaluation methodologies in text generation. Our codebase, datasets, and models are publicly available.

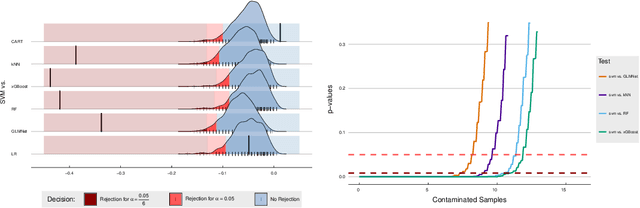
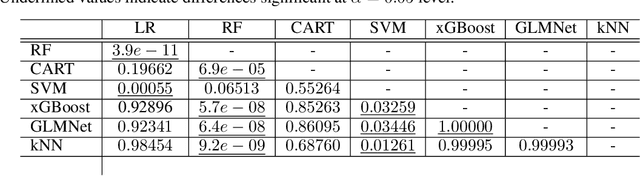
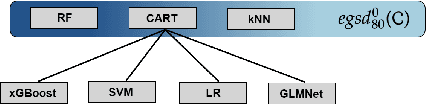
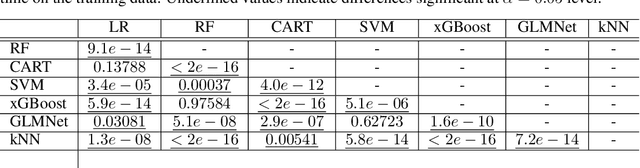
Statistical Multicriteria Benchmarking via the GSD-Front

Given the vast number of classifiers that have been (and continue to be) proposed, reliable methods for comparing them are becoming increasingly important. The desire for reliability is broken down into three main aspects: (1) Comparisons should allow for different quality metrics simultaneously. (2) Comparisons should take into account the statistical uncertainty induced by the choice of benchmark suite. (3) The robustness of the comparisons under small deviations in the underlying assumptions should be verifiable. To address (1), we propose to compare classifiers using a generalized stochastic dominance ordering (GSD) and present the GSD-front as an information-efficient alternative to the classical Pareto-front. For (2), we propose a consistent statistical estimator for the GSD-front and construct a statistical test for whether a (potentially new) classifier lies in the GSD-front of a set of state-of-the-art classifiers. For (3), we relax our proposed test using techniques from robust statistics and imprecise probabilities. We illustrate our concepts on the benchmark suite PMLB and on the platform OpenML.

Partial Rankings of Optimizers

We introduce a framework for benchmarking optimizers according to multiple criteria over various test functions. Based on a recently introduced union-free generic depth function for partial orders/rankings, it fully exploits the ordinal information and allows for incomparability. Our method describes the distribution of all partial orders/rankings, avoiding the notorious shortcomings of aggregation. This permits to identify test functions that produce central or outlying rankings of optimizers and to assess the quality of benchmarking suites.

Comparing Machine Learning Algorithms by Union-Free Generic Depth

We propose a framework for descriptively analyzing sets of partial orders based on the concept of depth functions. Despite intensive studies in linear and metric spaces, there is very little discussion on depth functions for non-standard data types such as partial orders. We introduce an adaptation of the well-known simplicial depth to the set of all partial orders, the union-free generic (ufg) depth. Moreover, we utilize our ufg depth for a comparison of machine learning algorithms based on multidimensional performance measures. Concretely, we provide two examples of classifier comparisons on samples of standard benchmark data sets. Our results demonstrate promisingly the wide variety of different analysis approaches based on ufg methods. Furthermore, the examples outline that our approach differs substantially from existing benchmarking approaches, and thus adds a new perspective to the vivid debate on classifier comparison.

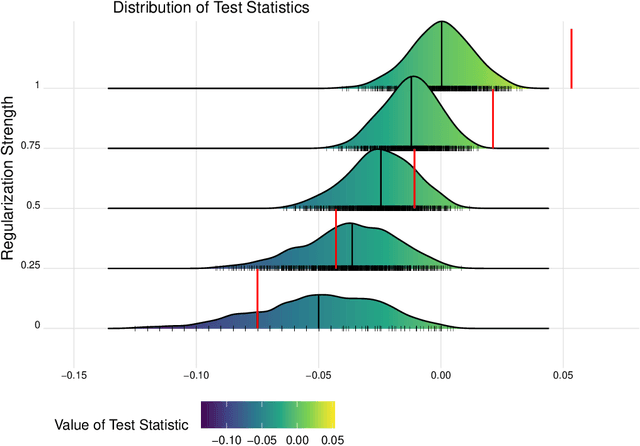
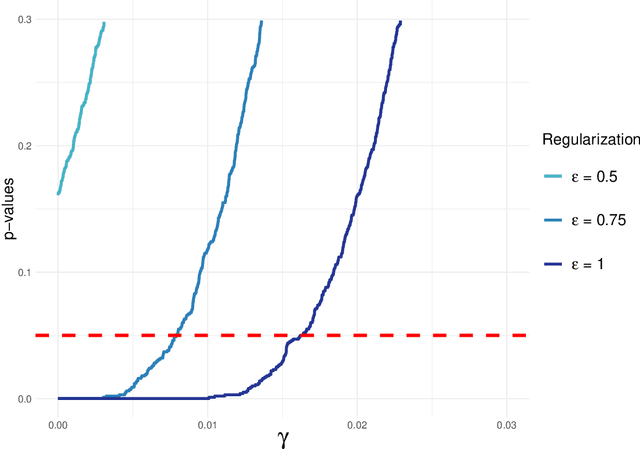
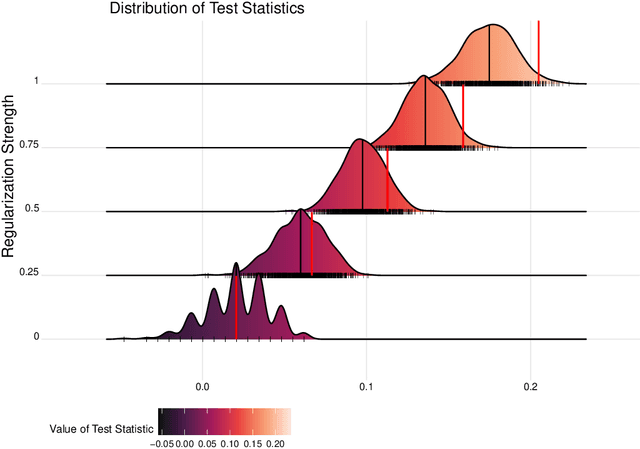
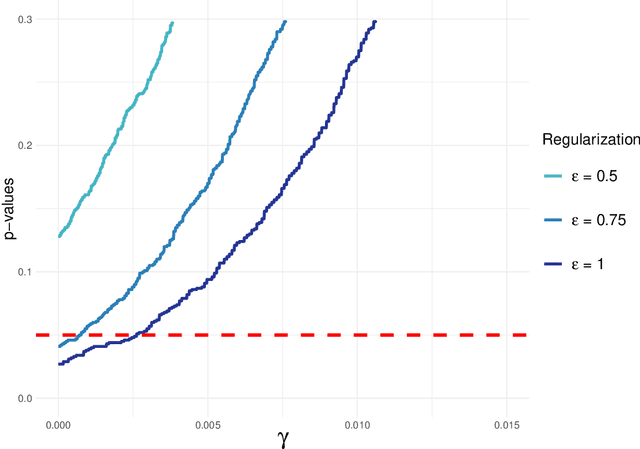
Robust Statistical Comparison of Random Variables with Locally Varying Scale of Measurement

Spaces with locally varying scale of measurement, like multidimensional structures with differently scaled dimensions, are pretty common in statistics and machine learning. Nevertheless, it is still understood as an open question how to exploit the entire information encoded in them properly. We address this problem by considering an order based on (sets of) expectations of random variables mapping into such non-standard spaces. This order contains stochastic dominance and expectation order as extreme cases when no, or respectively perfect, cardinal structure is given. We derive a (regularized) statistical test for our proposed generalized stochastic dominance (GSD) order, operationalize it by linear optimization, and robustify it by imprecise probability models. Our findings are illustrated with data from multidimensional poverty measurement, finance, and medicine.

A note on the connectedness property of union-free generic sets of partial orders

This short note describes and proves a connectedness property which was introduced in Blocher et al. [2023] in the context of data depth functions for partial orders. The connectedness property gives a structural insight into union-free generic sets. These sets, presented in Blocher et al. [2023], are defined by using a closure operator on the set of all partial orders which naturally appears within the theory of formal concept analysis. In the language of formal concept analysis, the property of connectedness can be vividly proven. However, since within Blocher et al. [2023] we did not discuss formal concept analysis, we outsourced the proof to this note.

Depth Functions for Partial Orders with a Descriptive Analysis of Machine Learning Algorithms

We propose a framework for descriptively analyzing sets of partial orders based on the concept of depth functions. Despite intensive studies of depth functions in linear and metric spaces, there is very little discussion on depth functions for non-standard data types such as partial orders. We introduce an adaptation of the well-known simplicial depth to the set of all partial orders, the union-free generic (ufg) depth. Moreover, we utilize our ufg depth for a comparison of machine learning algorithms based on multidimensional performance measures. Concretely, we analyze the distribution of different classifier performances over a sample of standard benchmark data sets. Our results promisingly demonstrate that our approach differs substantially from existing benchmarking approaches and, therefore, adds a new perspective to the vivid debate on the comparison of classifiers.

Information efficient learning of complexly structured preferences: Elicitation procedures and their application to decision making under uncertainty

In this paper we propose efficient methods for elicitation of complexly structured preferences and utilize these in problems of decision making under (severe) uncertainty. Based on the general framework introduced in Jansen, Schollmeyer and Augustin (2018, Int. J. Approx. Reason), we now design elicitation procedures and algorithms that enable decision makers to reveal their underlying preference system (i.e. two relations, one encoding the ordinal, the other the cardinal part of the preferences) while having to answer as few as possible simple ranking questions. Here, two different approaches are followed. The first approach directly utilizes the collected ranking data for obtaining the ordinal part of the preferences, while their cardinal part is constructed implicitly by measuring meta data on the decision maker's consideration times. In contrast, the second approach explicitly elicits also the cardinal part of the decision maker's preference system, however, only an approximate version of it. This approximation is obtained by additionally collecting labels of preference strength during the elicitation procedure. For both approaches, we give conditions under which they produce the decision maker's true preference system and investigate how their efficiency can be improved. For the latter purpose, besides data-free approaches, we also discuss ways for effectively guiding the elicitation procedure if data from previous elicitation rounds is available. Finally, we demonstrate how the proposed elicitation methods can be utilized in problems of decision under (severe) uncertainty. Precisely, we show that under certain conditions optimal decisions can be found without fully specifying the preference system.