Beyond algorithm hyperparameters: on preprocessing hyperparameters and associated pitfalls in machine learning applications

Adequately generating and evaluating prediction models based on supervised machine learning (ML) is often challenging, especially for less experienced users in applied research areas. Special attention is required in settings where the model generation process involves hyperparameter tuning, i.e. data-driven optimization of different types of hyperparameters to improve the predictive performance of the resulting model. Discussions about tuning typically focus on the hyperparameters of the ML algorithm (e.g., the minimum number of observations in each terminal node for a tree-based algorithm). In this context, it is often neglected that hyperparameters also exist for the preprocessing steps that are applied to the data before it is provided to the algorithm (e.g., how to handle missing feature values in the data). As a consequence, users experimenting with different preprocessing options to improve model performance may be unaware that this constitutes a form of hyperparameter tuning - albeit informal and unsystematic - and thus may fail to report or account for this optimization. To illuminate this issue, this paper reviews and empirically illustrates different procedures for generating and evaluating prediction models, explicitly addressing the different ways algorithm and preprocessing hyperparameters are typically handled by applied ML users. By highlighting potential pitfalls, especially those that may lead to exaggerated performance claims, this review aims to further improve the quality of predictive modeling in ML applications.

Constructing Confidence Intervals for 'the' Generalization Error -- a Comprehensive Benchmark Study

When assessing the quality of prediction models in machine learning, confidence intervals (CIs) for the generalization error, which measures predictive performance, are a crucial tool. Luckily, there exist many methods for computing such CIs and new promising approaches are continuously being proposed. Typically, these methods combine various resampling procedures, most popular among them cross-validation and bootstrapping, with different variance estimation techniques. Unfortunately, however, there is currently no consensus on when any of these combinations may be most reliably employed and how they generally compare. In this work, we conduct the first large-scale study comparing CIs for the generalization error - empirically evaluating 13 different methods on a total of 18 tabular regression and classification problems, using four different inducers and a total of eight loss functions. We give an overview of the methodological foundations and inherent challenges of constructing CIs for the generalization error and provide a concise review of all 13 methods in a unified framework. Finally, the CI methods are evaluated in terms of their relative coverage frequency, width, and runtime. Based on these findings, we are able to identify a subset of methods that we would recommend. We also publish the datasets as a benchmarking suite on OpenML and our code on GitHub to serve as a basis for further studies.

Position Paper: Rethinking Empirical Research in Machine Learning: Addressing Epistemic and Methodological Challenges of Experimentation

We warn against a common but incomplete understanding of empirical research in machine learning (ML) that leads to non-replicable results, makes findings unreliable, and threatens to undermine progress in the field. To overcome this alarming situation, we call for more awareness of the plurality of ways of gaining knowledge experimentally but also of some epistemic limitations. In particular, we argue most current empirical ML research is fashioned as confirmatory research while it should rather be considered exploratory.

Understanding random forests and overfitting: a visualization and simulation study

Random forests have become popular for clinical risk prediction modelling. In a case study on predicting ovarian malignancy, we observed training c-statistics close to 1. Although this suggests overfitting, performance was competitive on test data. We aimed to understand the behaviour of random forests by (1) visualizing data space in three real world case studies and (2) a simulation study. For the case studies, risk estimates were visualised using heatmaps in a 2-dimensional subspace. The simulation study included 48 logistic data generating mechanisms (DGM), varying the predictor distribution, the number of predictors, the correlation between predictors, the true c-statistic and the strength of true predictors. For each DGM, 1000 training datasets of size 200 or 4000 were simulated and RF models trained with minimum node size 2 or 20 using ranger package, resulting in 192 scenarios in total. The visualizations suggested that the model learned spikes of probability around events in the training set. A cluster of events created a bigger peak, isolated events local peaks. In the simulation study, median training c-statistics were between 0.97 and 1 unless there were 4 or 16 binary predictors with minimum node size 20. Median test c-statistics were higher with higher events per variable, higher minimum node size, and binary predictors. Median training slopes were always above 1, and were not correlated with median test slopes across scenarios (correlation -0.11). Median test slopes were higher with higher true c-statistic, higher minimum node size, and higher sample size. Random forests learn local probability peaks that often yield near perfect training c-statistics without strongly affecting c-statistics on test data. When the aim is probability estimation, the simulation results go against the common recommendation to use fully grown trees in random forest models.

Evaluating machine learning models in non-standard settings: An overview and new findings

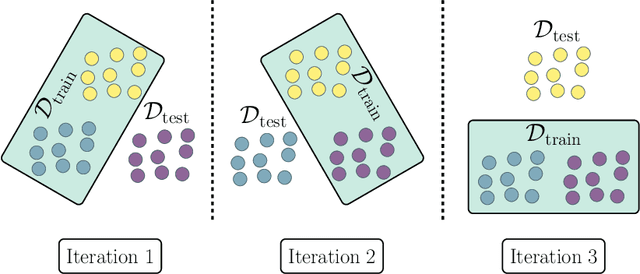
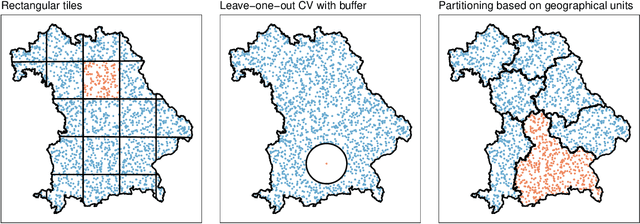
Estimating the generalization error (GE) of machine learning models is fundamental, with resampling methods being the most common approach. However, in non-standard settings, particularly those where observations are not independently and identically distributed, resampling using simple random data divisions may lead to biased GE estimates. This paper strives to present well-grounded guidelines for GE estimation in various such non-standard settings: clustered data, spatial data, unequal sampling probabilities, concept drift, and hierarchically structured outcomes. Our overview combines well-established methodologies with other existing methods that, to our knowledge, have not been frequently considered in these particular settings. A unifying principle among these techniques is that the test data used in each iteration of the resampling procedure should reflect the new observations to which the model will be applied, while the training data should be representative of the entire data set used to obtain the final model. Beyond providing an overview, we address literature gaps by conducting simulation studies. These studies assess the necessity of using GE-estimation methods tailored to the respective setting. Our findings corroborate the concern that standard resampling methods often yield biased GE estimates in non-standard settings, underscoring the importance of tailored GE estimation.

Prediction approaches for partly missing multi-omics covariate data: A literature review and an empirical comparison study

As the availability of omics data has increased in the last few years, more multi-omics data have been generated, that is, high-dimensional molecular data consisting of several types such as genomic, transcriptomic, or proteomic data, all obtained from the same patients. Such data lend themselves to being used as covariates in automatic outcome prediction because each omics type may contribute unique information, possibly improving predictions compared to using only one omics data type. Frequently, however, in the training data and the data to which automatic prediction rules should be applied, the test data, the different omics data types are not available for all patients. We refer to this type of data as block-wise missing multi-omics data. First, we provide a literature review on existing prediction methods applicable to such data. Subsequently, using a collection of 13 publicly available multi-omics data sets, we compare the predictive performances of several of these approaches for different block-wise missingness patterns. Finally, we discuss the results of this empirical comparison study and draw some tentative conclusions.

Hyperparameter Optimization: Foundations, Algorithms, Best Practices and Open Challenges

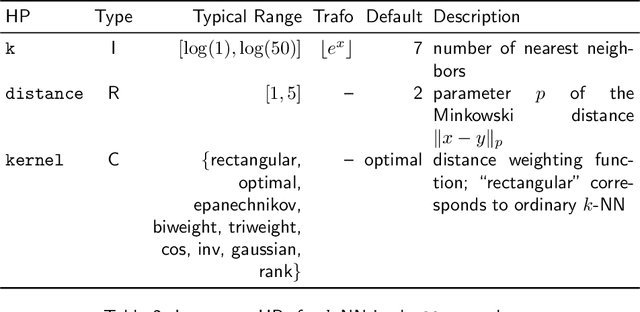
Most machine learning algorithms are configured by one or several hyperparameters that must be carefully chosen and often considerably impact performance. To avoid a time consuming and unreproducible manual trial-and-error process to find well-performing hyperparameter configurations, various automatic hyperparameter optimization (HPO) methods, e.g., based on resampling error estimation for supervised machine learning, can be employed. After introducing HPO from a general perspective, this paper reviews important HPO methods such as grid or random search, evolutionary algorithms, Bayesian optimization, Hyperband and racing. It gives practical recommendations regarding important choices to be made when conducting HPO, including the HPO algorithms themselves, performance evaluation, how to combine HPO with ML pipelines, runtime improvements, and parallelization.

Large-scale benchmark study of survival prediction methods using multi-omics data

Multi-omics data, that is, datasets containing different types of high-dimensional molecular variables (often in addition to classical clinical variables), are increasingly generated for the investigation of various diseases. Nevertheless, questions remain regarding the usefulness of multi-omics data for the prediction of disease outcomes such as survival time. It is also unclear which methods are most appropriate to derive such prediction models. We aim to give some answers to these questions by means of a large-scale benchmark study using real data. Different prediction methods from machine learning and statistics were applied on 18 multi-omics cancer datasets from the database "The Cancer Genome Atlas", containing from 35 to 1,000 observations and from 60,000 to 100,000 variables. The considered outcome was the (censored) survival time. Twelve methods based on boosting, penalized regression and random forest were compared, comprising both methods that do and that do not take the group structure of the omics variables into account. The Kaplan-Meier estimate and a Cox model using only clinical variables were used as reference methods. The methods were compared using several repetitions of 5-fold cross-validation. Uno's C-index and the integrated Brier-score served as performance metrics. The results show that, although multi-omics data can improve the prediction performance, this is not generally the case. Only the method block forest slightly outperformed the Cox model on average over all datasets. Taking into account the multi-omics structure improves the predictive performance and protects variables in low-dimensional groups - especially clinical variables - from not being included in the model. All analyses are reproducible using freely available R code.

Tunability: Importance of Hyperparameters of Machine Learning Algorithms

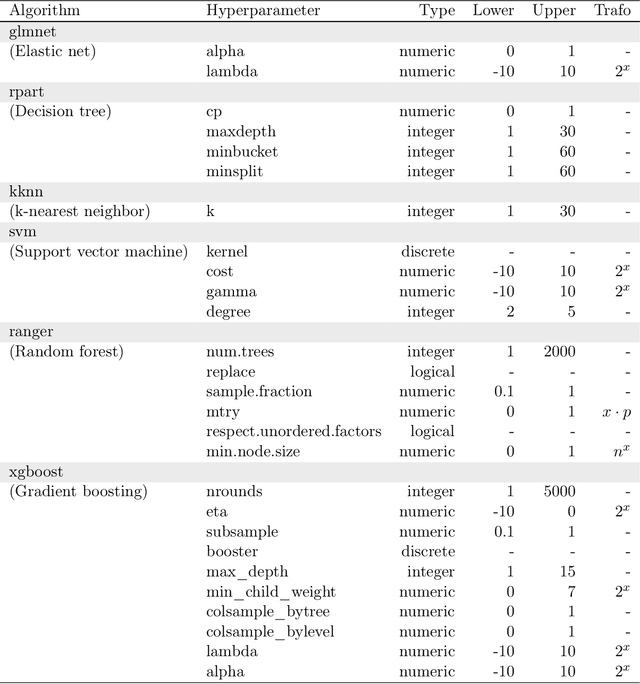
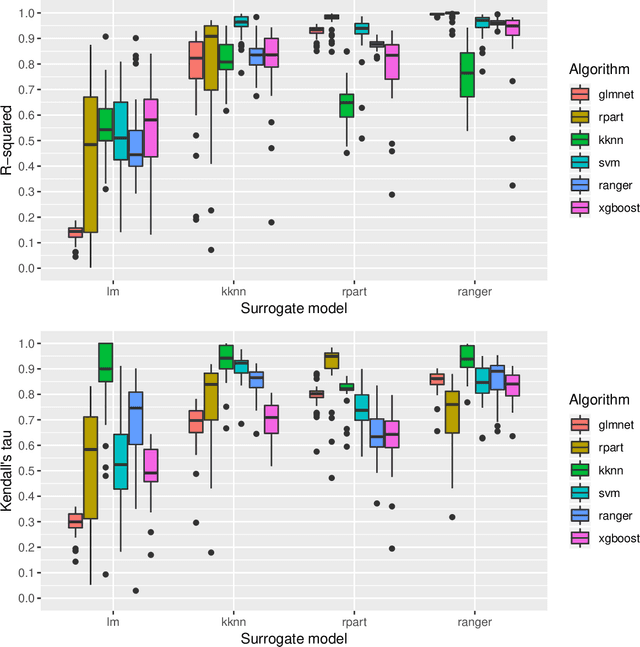
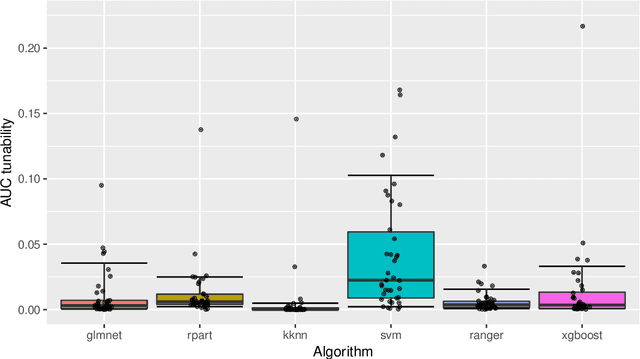
Modern supervised machine learning algorithms involve hyperparameters that have to be set before running them. Options for setting hyperparameters are default values from the software package, manual configuration by the user or configuring them for optimal predictive performance by a tuning procedure. The goal of this paper is two-fold. Firstly, we formalize the problem of tuning from a statistical point of view, define data-based defaults and suggest general measures quantifying the tunability of hyperparameters of algorithms. Secondly, we conduct a large-scale benchmarking study based on 38 datasets from the OpenML platform and six common machine learning algorithms. We apply our measures to assess the tunability of their parameters. Our results yield default values for hyperparameters and enable users to decide whether it is worth conducting a possibly time consuming tuning strategy, to focus on the most important hyperparameters and to chose adequate hyperparameter spaces for tuning.

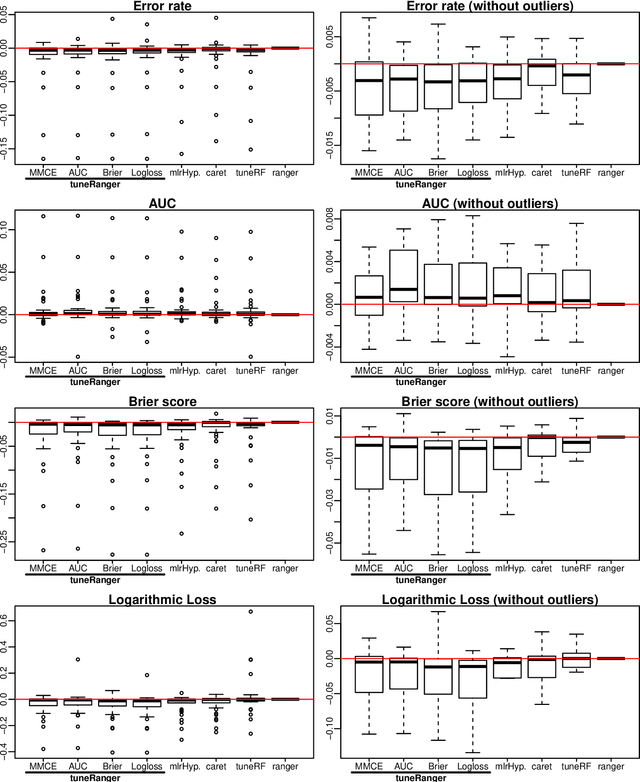
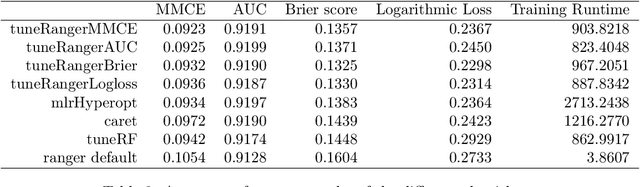
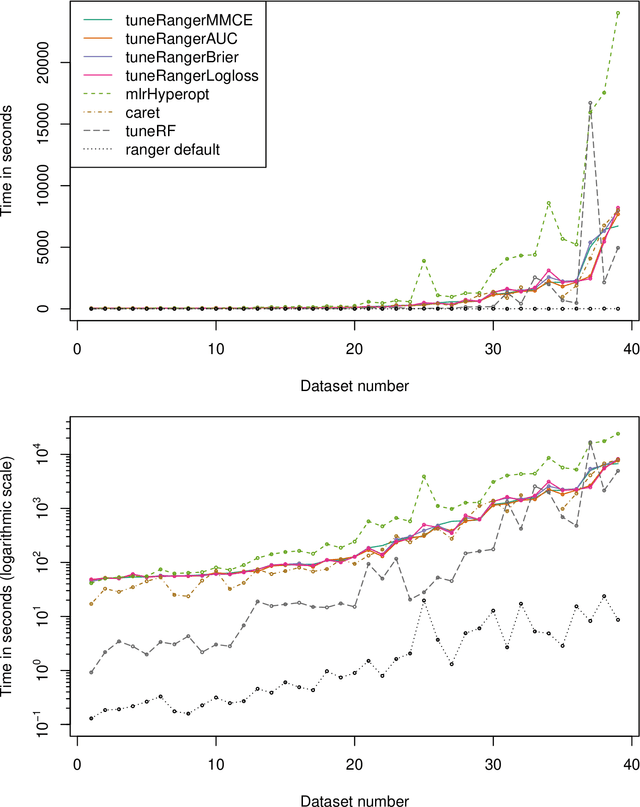
Hyperparameters and Tuning Strategies for Random Forest

The random forest algorithm (RF) has several hyperparameters that have to be set by the user, e.g., the number of observations drawn randomly for each tree and whether they are drawn with or without replacement, the number of variables drawn randomly for each split, the splitting rule, the minimum number of samples that a node must contain and the number of trees. In this paper, we first provide a literature review on the parameters' influence on the prediction performance and on variable importance measures, also considering interactions between hyperparameters. It is well known that in most cases RF works reasonably well with the default values of the hyperparameters specified in software packages. Nevertheless, tuning the hyperparameters can improve the performance of RF. In the second part of this paper, after a brief overview of tuning strategies we demonstrate the application of one of the most established tuning strategies, model-based optimization (MBO). To make it easier to use, we provide the tuneRanger R package that tunes RF with MBO automatically. In a benchmark study on several datasets, we compare the prediction performance and runtime of tuneRanger with other tuning implementations in R and RF with default hyperparameters.