Constructing Confidence Intervals for 'the' Generalization Error -- a Comprehensive Benchmark Study

When assessing the quality of prediction models in machine learning, confidence intervals (CIs) for the generalization error, which measures predictive performance, are a crucial tool. Luckily, there exist many methods for computing such CIs and new promising approaches are continuously being proposed. Typically, these methods combine various resampling procedures, most popular among them cross-validation and bootstrapping, with different variance estimation techniques. Unfortunately, however, there is currently no consensus on when any of these combinations may be most reliably employed and how they generally compare. In this work, we conduct the first large-scale study comparing CIs for the generalization error - empirically evaluating 13 different methods on a total of 18 tabular regression and classification problems, using four different inducers and a total of eight loss functions. We give an overview of the methodological foundations and inherent challenges of constructing CIs for the generalization error and provide a concise review of all 13 methods in a unified framework. Finally, the CI methods are evaluated in terms of their relative coverage frequency, width, and runtime. Based on these findings, we are able to identify a subset of methods that we would recommend. We also publish the datasets as a benchmarking suite on OpenML and our code on GitHub to serve as a basis for further studies.

Multi forests: Variable importance for multi-class outcomes

In prediction tasks with multi-class outcomes, identifying covariates specifically associated with one or more outcome classes can be important. Conventional variable importance measures (VIMs) from random forests (RFs), like permutation and Gini importance, focus on overall predictive performance or node purity, without differentiating between the classes. Therefore, they can be expected to fail to distinguish class-associated covariates from covariates that only distinguish between groups of classes. We introduce a VIM called multi-class VIM, tailored for identifying exclusively class-associated covariates, via a novel RF variant called multi forests (MuFs). The trees in MuFs use both multi-way and binary splitting. The multi-way splits generate child nodes for each class, using a split criterion that evaluates how well these nodes represent their respective classes. This setup forms the basis of the multi-class VIM, which measures the discriminatory ability of the splits performed in the respective covariates with regard to this split criterion. Alongside the multi-class VIM, we introduce a second VIM, the discriminatory VIM. This measure, based on the binary splits, assesses the strength of the general influence of the covariates, irrespective of their class-associatedness. Simulation studies demonstrate that the multi-class VIM specifically ranks class-associated covariates highly, unlike conventional VIMs which also rank other types of covariates highly. Analyses of 121 datasets reveal that MuFs often have slightly lower predictive performance compared to conventional RFs. This is, however, not a limiting factor given the algorithm's primary purpose of calculating the multi-class VIM.

Evaluating machine learning models in non-standard settings: An overview and new findings

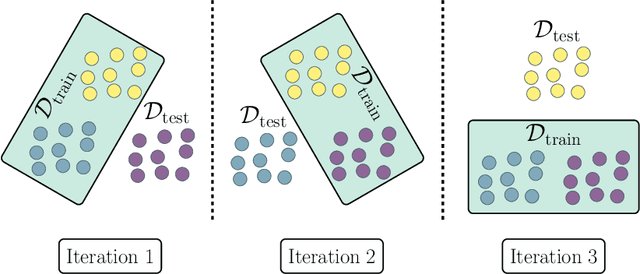
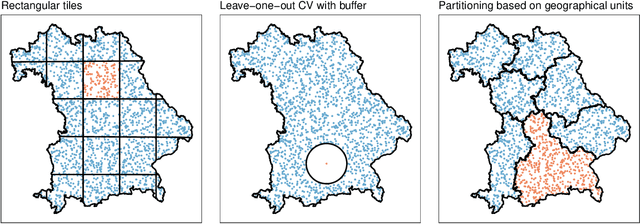
Estimating the generalization error (GE) of machine learning models is fundamental, with resampling methods being the most common approach. However, in non-standard settings, particularly those where observations are not independently and identically distributed, resampling using simple random data divisions may lead to biased GE estimates. This paper strives to present well-grounded guidelines for GE estimation in various such non-standard settings: clustered data, spatial data, unequal sampling probabilities, concept drift, and hierarchically structured outcomes. Our overview combines well-established methodologies with other existing methods that, to our knowledge, have not been frequently considered in these particular settings. A unifying principle among these techniques is that the test data used in each iteration of the resampling procedure should reflect the new observations to which the model will be applied, while the training data should be representative of the entire data set used to obtain the final model. Beyond providing an overview, we address literature gaps by conducting simulation studies. These studies assess the necessity of using GE-estimation methods tailored to the respective setting. Our findings corroborate the concern that standard resampling methods often yield biased GE estimates in non-standard settings, underscoring the importance of tailored GE estimation.

Prediction approaches for partly missing multi-omics covariate data: A literature review and an empirical comparison study

As the availability of omics data has increased in the last few years, more multi-omics data have been generated, that is, high-dimensional molecular data consisting of several types such as genomic, transcriptomic, or proteomic data, all obtained from the same patients. Such data lend themselves to being used as covariates in automatic outcome prediction because each omics type may contribute unique information, possibly improving predictions compared to using only one omics data type. Frequently, however, in the training data and the data to which automatic prediction rules should be applied, the test data, the different omics data types are not available for all patients. We refer to this type of data as block-wise missing multi-omics data. First, we provide a literature review on existing prediction methods applicable to such data. Subsequently, using a collection of 13 publicly available multi-omics data sets, we compare the predictive performances of several of these approaches for different block-wise missingness patterns. Finally, we discuss the results of this empirical comparison study and draw some tentative conclusions.

Sequential Permutation Testing of Random Forest Variable Importance Measures

Hypothesis testing of random forest (RF) variable importance measures (VIMP) remains the subject of ongoing research. Among recent developments, heuristic approaches to parametric testing have been proposed whose distributional assumptions are based on empirical evidence. Other formal tests under regularity conditions were derived analytically. However, these approaches can be computationally expensive or even practically infeasible. This problem also occurs with non-parametric permutation tests, which are, however, distribution-free and can generically be applied to any type of RF and VIMP. Embracing this advantage, it is proposed here to use sequential permutation tests and sequential p-value estimation to reduce the high computational costs associated with conventional permutation tests. The popular and widely used permutation VIMP serves as a practical and relevant application example. The results of simulation studies confirm that the theoretical properties of the sequential tests apply, that is, the type-I error probability is controlled at a nominal level and a high power is maintained with considerably fewer permutations needed in comparison to conventional permutation testing. The numerical stability of the methods is investigated in two additional application studies. In summary, theoretically sound sequential permutation testing of VIMP is possible at greatly reduced computational costs. Recommendations for application are given. A respective implementation is provided through the accompanying R package $rfvimptest$. The approach can also be easily applied to any kind of prediction model.

Large-scale benchmark study of survival prediction methods using multi-omics data

Multi-omics data, that is, datasets containing different types of high-dimensional molecular variables (often in addition to classical clinical variables), are increasingly generated for the investigation of various diseases. Nevertheless, questions remain regarding the usefulness of multi-omics data for the prediction of disease outcomes such as survival time. It is also unclear which methods are most appropriate to derive such prediction models. We aim to give some answers to these questions by means of a large-scale benchmark study using real data. Different prediction methods from machine learning and statistics were applied on 18 multi-omics cancer datasets from the database "The Cancer Genome Atlas", containing from 35 to 1,000 observations and from 60,000 to 100,000 variables. The considered outcome was the (censored) survival time. Twelve methods based on boosting, penalized regression and random forest were compared, comprising both methods that do and that do not take the group structure of the omics variables into account. The Kaplan-Meier estimate and a Cox model using only clinical variables were used as reference methods. The methods were compared using several repetitions of 5-fold cross-validation. Uno's C-index and the integrated Brier-score served as performance metrics. The results show that, although multi-omics data can improve the prediction performance, this is not generally the case. Only the method block forest slightly outperformed the Cox model on average over all datasets. Taking into account the multi-omics structure improves the predictive performance and protects variables in low-dimensional groups - especially clinical variables - from not being included in the model. All analyses are reproducible using freely available R code.

A U-statistic estimator for the variance of resampling-based error estimators

We revisit resampling procedures for error estimation in binary classification in terms of U-statistics. In particular, we exploit the fact that the error rate estimator involving all learning-testing splits is a U-statistic. Thus, it has minimal variance among all unbiased estimators and is asymptotically normally distributed. Moreover, there is an unbiased estimator for this minimal variance if the total sample size is at least the double learning set size plus two. In this case, we exhibit such an estimator which is another U-statistic. It enjoys, again, various optimality properties and yields an asymptotically exact hypothesis test of the equality of error rates when two learning algorithms are compared. Our statements apply to any deterministic learning algorithms under weak non-degeneracy assumptions.