ProDAG: Projection-induced variational inference for directed acyclic graphs

Directed acyclic graph (DAG) learning is a rapidly expanding field of research. Though the field has witnessed remarkable advances over the past few years, it remains statistically and computationally challenging to learn a single (point estimate) DAG from data, let alone provide uncertainty quantification. Our article addresses the difficult task of quantifying graph uncertainty by developing a variational Bayes inference framework based on novel distributions that have support directly on the space of DAGs. The distributions, which we use to form our prior and variational posterior, are induced by a projection operation, whereby an arbitrary continuous distribution is projected onto the space of sparse weighted acyclic adjacency matrices (matrix representations of DAGs) with probability mass on exact zeros. Though the projection constitutes a combinatorial optimization problem, it is solvable at scale via recently developed techniques that reformulate acyclicity as a continuous constraint. We empirically demonstrate that our method, ProDAG, can deliver accurate inference, and often outperforms existing state-of-the-art alternatives.

Contextual directed acyclic graphs

Estimating the structure of directed acyclic graphs (DAGs) from observational data remains a significant challenge in machine learning. Most research in this area concentrates on learning a single DAG for the entire population. This paper considers an alternative setting where the graph structure varies across individuals based on available "contextual" features. We tackle this contextual DAG problem via a neural network that maps the contextual features to a DAG, represented as a weighted adjacency matrix. The neural network is equipped with a novel projection layer that ensures the output matrices are sparse and satisfy a recently developed characterization of acyclicity. We devise a scalable computational framework for learning contextual DAGs and provide a convergence guarantee and an analytical gradient for backpropagating through the projection layer. Our experiments suggest that the new approach can recover the true context-specific graph where existing approaches fail.

DeepVol: A Deep Transfer Learning Approach for Universal Asset Volatility Modeling

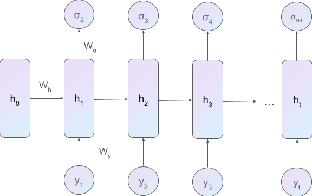
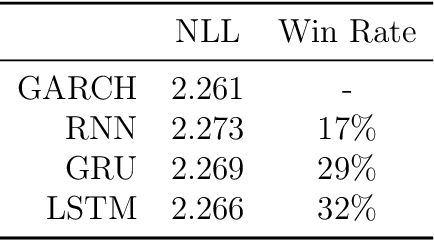
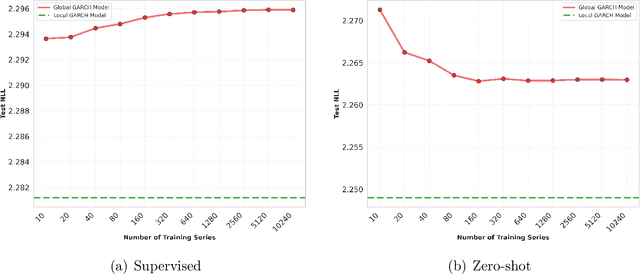
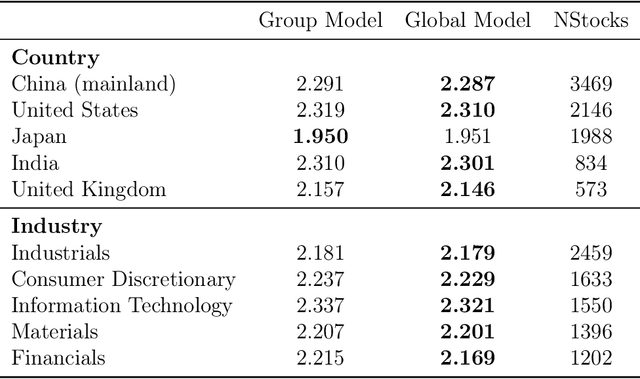
This paper introduces DeepVol, a promising new deep learning volatility model that outperforms traditional econometric models in terms of model generality. DeepVol leverages the power of transfer learning to effectively capture and model the volatility dynamics of all financial assets, including previously unseen ones, using a single universal model. This contrasts to the prevailing practice in econometrics literature, which necessitates training separate models for individual datasets. The introduction of DeepVol opens up new avenues for volatility modeling and forecasting in the finance industry, potentially transforming the way volatility is understood and predicted.

Particle Mean Field Variational Bayes

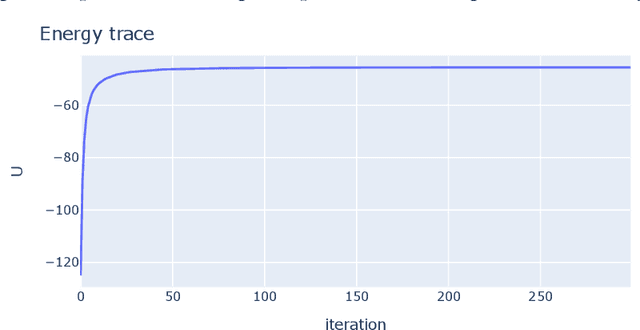
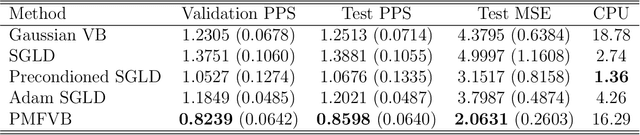
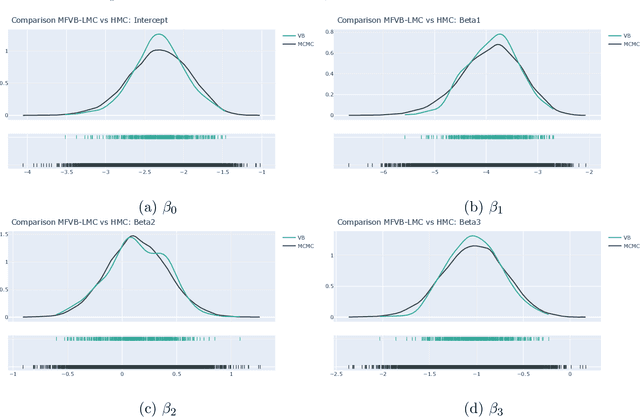
The Mean Field Variational Bayes (MFVB) method is one of the most computationally efficient techniques for Bayesian inference. However, its use has been restricted to models with conjugate priors or those that require analytical calculations. This paper proposes a novel particle-based MFVB approach that greatly expands the applicability of the MFVB method. We establish the theoretical basis of the new method by leveraging the connection between Wasserstein gradient flows and Langevin diffusion dynamics, and demonstrate the effectiveness of this approach using Bayesian logistic regression, stochastic volatility, and deep neural networks.

Realized recurrent conditional heteroskedasticity model for volatility modelling

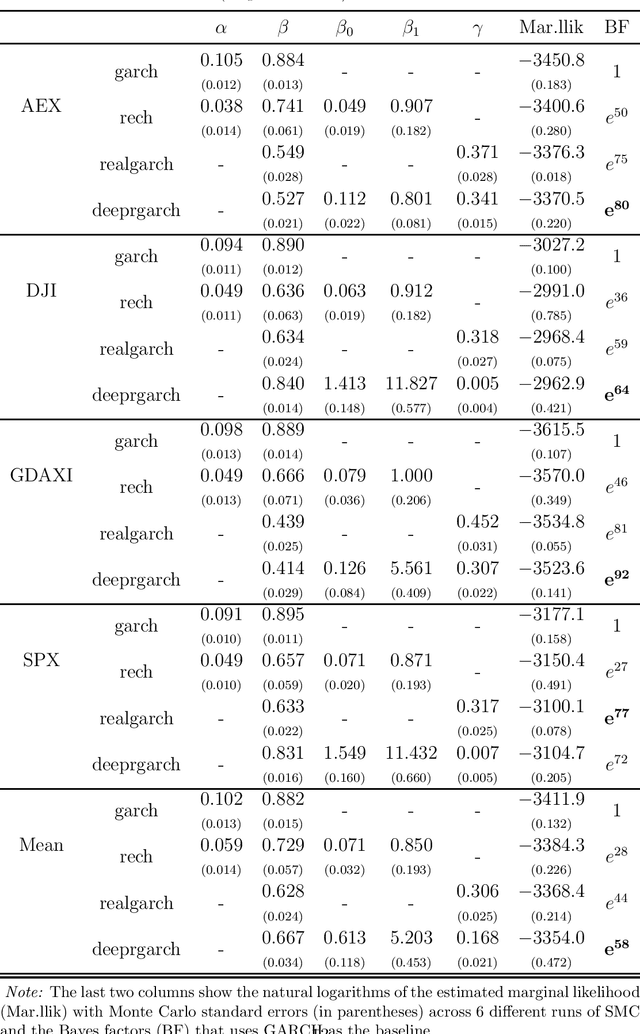
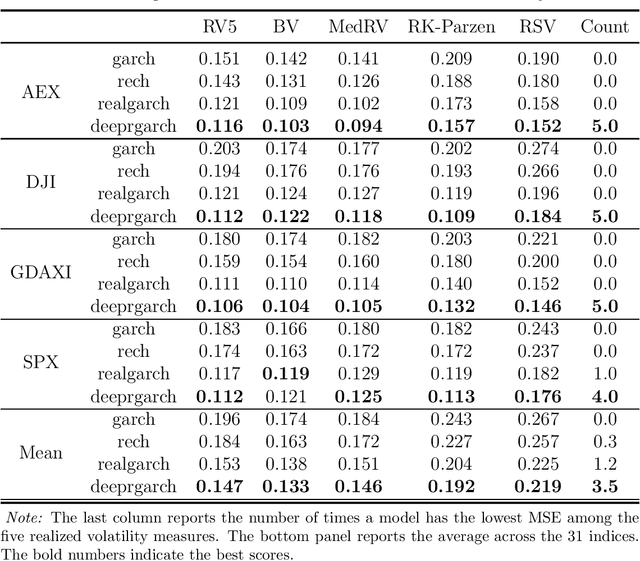
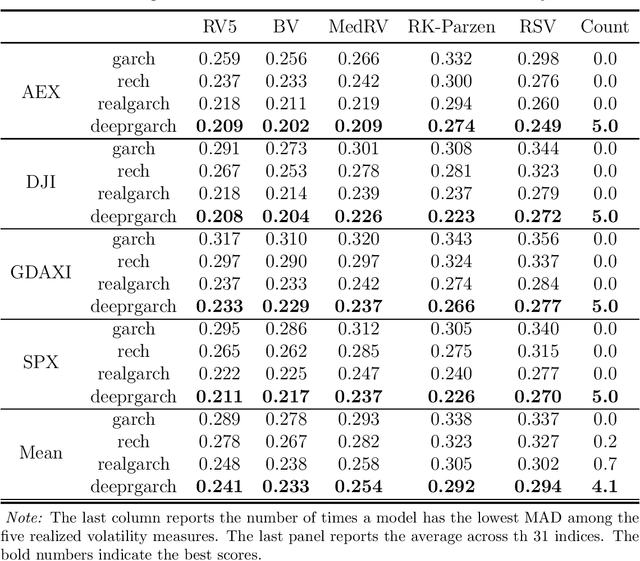
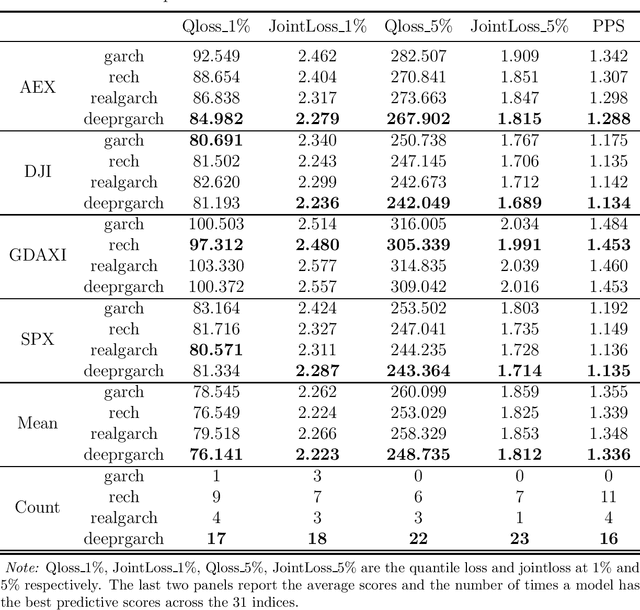
We propose a new approach to volatility modelling by combining deep learning (LSTM) and realized volatility measures. This LSTM-enhanced realized GARCH framework incorporates and distills modeling advances from financial econometrics, high frequency trading data and deep learning. Bayesian inference via the Sequential Monte Carlo method is employed for statistical inference and forecasting. The new framework can jointly model the returns and realized volatility measures, has an excellent in-sample fit and superior predictive performance compared to several benchmark models, while being able to adapt well to the stylized facts in volatility. The performance of the new framework is tested using a wide range of metrics, from marginal likelihood, volatility forecasting, to tail risk forecasting and option pricing. We report on a comprehensive empirical study using 31 widely traded stock indices over a time period that includes COVID-19 pandemic.

The Contextual Lasso: Sparse Linear Models via Deep Neural Networks

Sparse linear models are a gold standard tool for interpretable machine learning, a field of emerging importance as predictive models permeate decision-making in many domains. Unfortunately, sparse linear models are far less flexible as functions of their input features than black-box models like deep neural networks. With this capability gap in mind, we study a not-uncommon situation where the input features dichotomize into two groups: explanatory features, which we wish to explain the model's predictions, and contextual features, which we wish to determine the model's explanations. This dichotomy leads us to propose the contextual lasso, a new statistical estimator that fits a sparse linear model whose sparsity pattern and coefficients can vary with the contextual features. The fitting process involves learning a nonparametric map, realized via a deep neural network, from contextual feature vector to sparse coefficient vector. To attain sparse coefficients, we train the network with a novel lasso regularizer in the form of a projection layer that maps the network's output onto the space of $\ell_1$-constrained linear models. Extensive experiments on real and synthetic data suggest that the learned models, which remain highly transparent, can be sparser than the regular lasso without sacrificing the predictive power of a standard deep neural network.

Variance reduction properties of the reparameterization trick

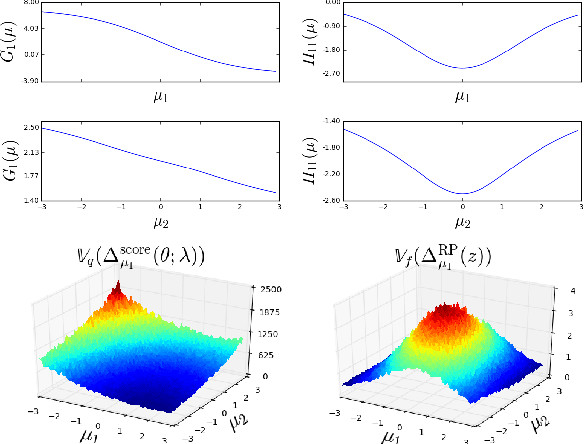
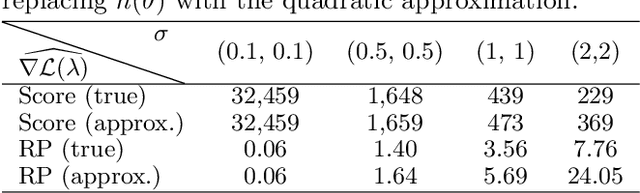
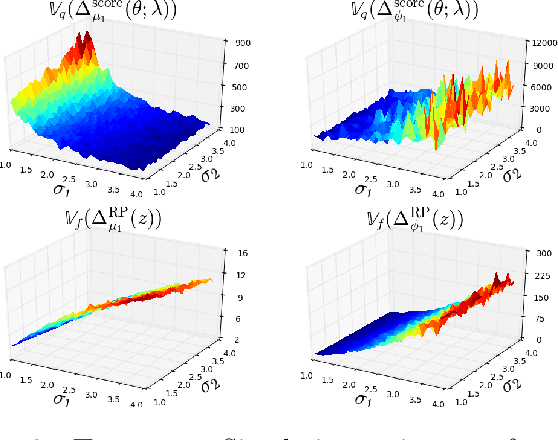
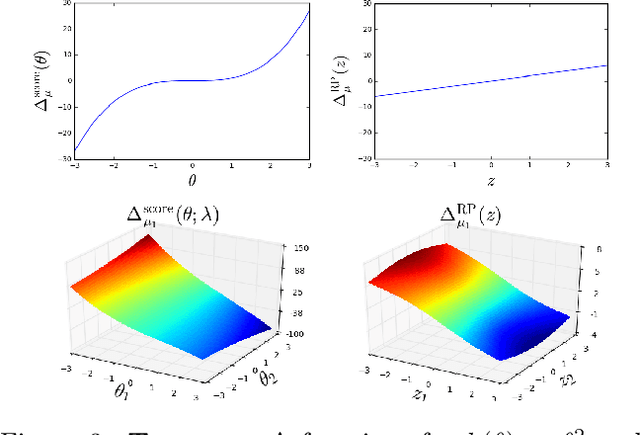
The reparameterization trick is widely used in variational inference as it yields more accurate estimates of the gradient of the variational objective than alternative approaches such as the score function method. Although there is overwhelming empirical evidence in the literature showing its success, there is relatively little research exploring why the reparameterization trick is so effective. We explore this under the idealized assumptions that the variational approximation is a mean-field Gaussian density and that the log of the joint density of the model parameters and the data is a quadratic function that depends on the variational mean. From this, we show that the marginal variances of the reparameterization gradient estimator are smaller than those of the score function gradient estimator. We apply the result of our idealized analysis to real-world examples.

Subsampling MCMC - An introduction for the survey statistician

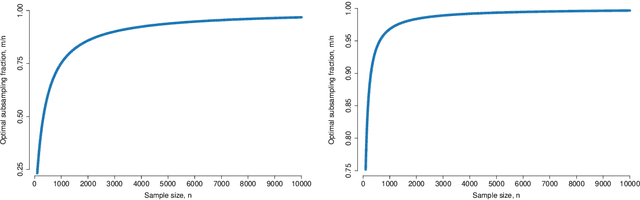
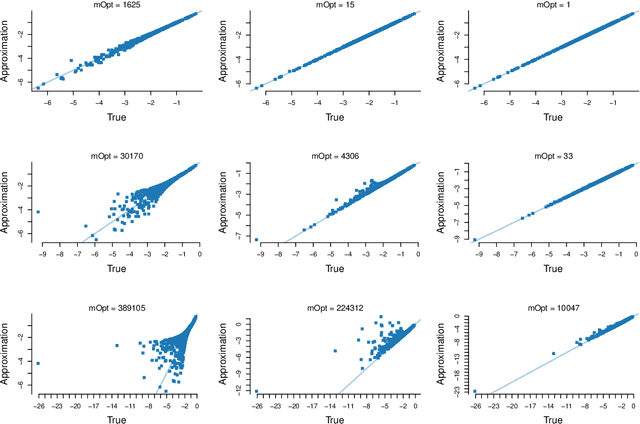
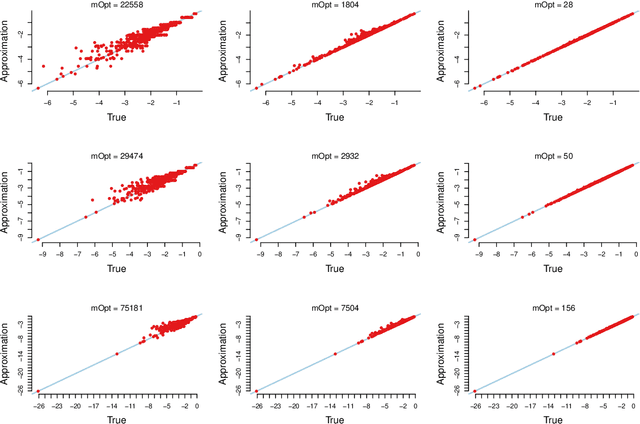
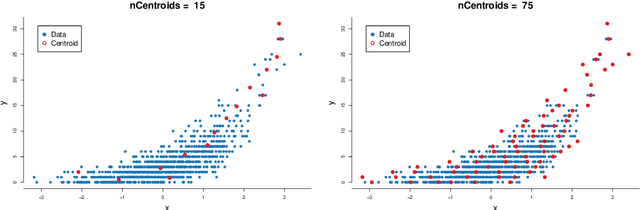
The rapid development of computing power and efficient Markov Chain Monte Carlo (MCMC) simulation algorithms have revolutionized Bayesian statistics, making it a highly practical inference method in applied work. However, MCMC algorithms tend to be computationally demanding, and are particularly slow for large datasets. Data subsampling has recently been suggested as a way to make MCMC methods scalable on massively large data, utilizing efficient sampling schemes and estimators from the survey sampling literature. These developments tend to be unknown by many survey statisticians who traditionally work with non-Bayesian methods, and rarely use MCMC. Our article explains the idea of data subsampling in MCMC by reviewing one strand of work, Subsampling MCMC, a so called pseudo-marginal MCMC approach to speeding up MCMC through data subsampling. The review is written for a survey statistician without previous knowledge of MCMC methods since our aim is to motivate survey sampling experts to contribute to the growing Subsampling MCMC literature.

Subsampling Sequential Monte Carlo for Static Bayesian Models

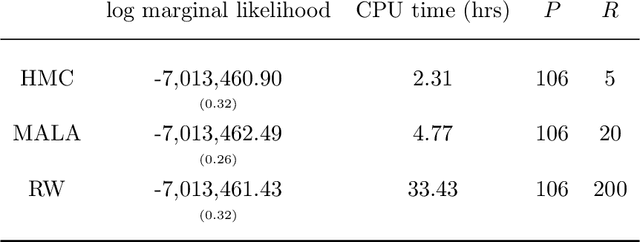
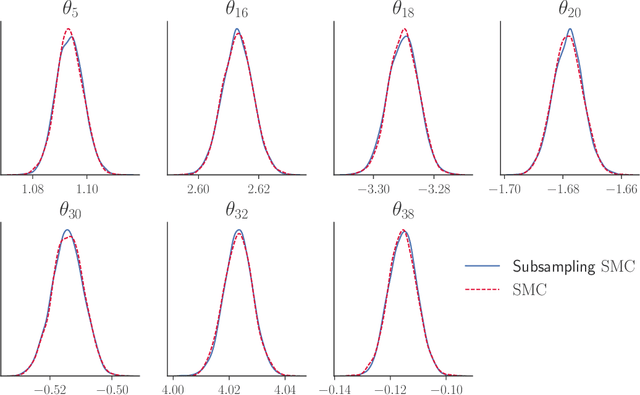
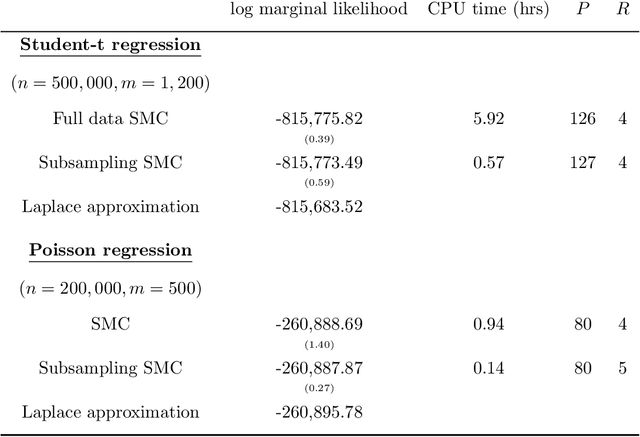
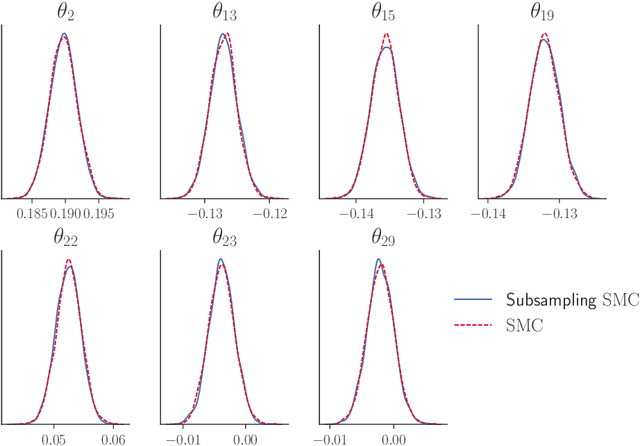
Our article shows how to carry out Bayesian inference by combining data subsampling with Sequential Monte Carlo (SMC). This takes advantage of the attractive properties of SMC for Bayesian computations with the ability of subsampling to tackle big data problems. SMC sequentially updates a cloud of particles through a sequence of densities, beginning with a density that is easy to sample from such as the prior and ending with the posterior density. Each update of the particle cloud consists of three steps: reweighting, resampling, and moving. In the move step, each particle is moved using a Markov kernel and this is typically the most computationally expensive part, particularly when the dataset is large. It is crucial to have an efficient move step to ensure particle diversity. Our article makes two important contributions. First, in order to speed up the SMC computation, we use an approximately unbiased and efficient annealed likelihood estimator based on data subsampling. The subsampling approach is more memory efficient than the corresponding full data SMC, which is a great advantage for parallel computation. Second, we use a Metropolis within Gibbs kernel with two conditional updates. First, a Hamiltonian Monte Carlo update makes distant moves for the model parameters. Second, a block pseudo-marginal proposal is used for the particles corresponding to the auxiliary variables for the data subsampling. We demonstrate the usefulness of the methodology using two large datasets.

Gaussian variational approximation for high-dimensional state space models

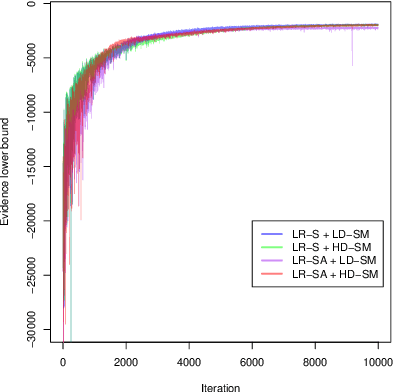
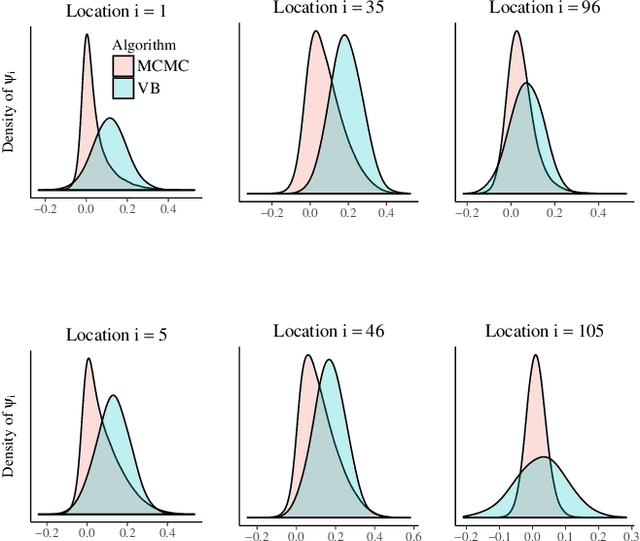
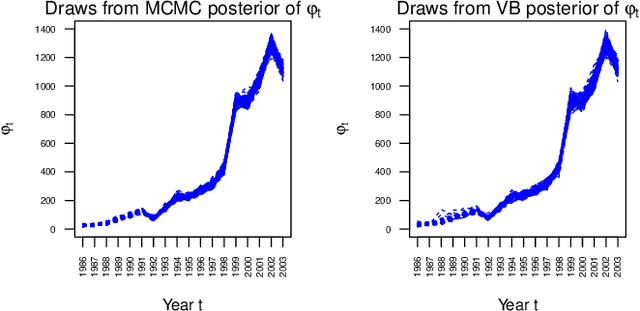
This article considers variational approximations of the posterior distribution in a high-dimensional state space model. The variational approximation is a multivariate Gaussian density, in which the variational parameters to be optimized are a mean vector and a covariance matrix. The number of parameters in the covariance matrix grows as the square of the number of model parameters, so it is necessary to find simple yet effective parametrizations of the covariance structure when the number of model parameters is large. The joint posterior distribution over the high-dimensional state vectors is approximated using a dynamic factor model, with Markovian dependence in time and a factor covariance structure for the states. This gives a reduced dimension description of the dependence structure for the states, as well as a temporal conditional independence structure similar to that in the true posterior. We illustrate our approach in two high-dimensional applications which are challenging for Markov chain Monte Carlo sampling. The first is a spatio-temporal model for the spread of the Eurasian Collared-Dove across North America. The second is a multivariate stochastic volatility model for financial returns via a Wishart process.