Autoencoder Enhanced Realised GARCH on Volatility Forecasting

Realised volatility has become increasingly prominent in volatility forecasting due to its ability to capture intraday price fluctuations. With a growing variety of realised volatility estimators, each with unique advantages and limitations, selecting an optimal estimator may introduce challenges. In this thesis, aiming to synthesise the impact of various realised volatility measures on volatility forecasting, we propose an extension of the Realised GARCH model that incorporates an autoencoder-generated synthetic realised measure, combining the information from multiple realised measures in a nonlinear manner. Our proposed model extends existing linear methods, such as Principal Component Analysis and Independent Component Analysis, to reduce the dimensionality of realised measures. The empirical evaluation, conducted across four major stock markets from January 2000 to June 2022 and including the period of COVID-19, demonstrates both the feasibility of applying an autoencoder to synthesise volatility measures and the superior effectiveness of the proposed model in one-step-ahead rolling volatility forecasting. The model exhibits enhanced flexibility in parameter estimations across each rolling window, outperforming traditional linear approaches. These findings indicate that nonlinear dimension reduction offers further adaptability and flexibility in improving the synthetic realised measure, with promising implications for future volatility forecasting applications.

Loss-based Bayesian Sequential Prediction of Value at Risk with a Long-Memory and Non-linear Realized Volatility Model

A long memory and non-linear realized volatility model class is proposed for direct Value at Risk (VaR) forecasting. This model, referred to as RNN-HAR, extends the heterogeneous autoregressive (HAR) model, a framework known for efficiently capturing long memory in realized measures, by integrating a Recurrent Neural Network (RNN) to handle non-linear dynamics. Loss-based generalized Bayesian inference with Sequential Monte Carlo is employed for model estimation and sequential prediction in RNN HAR. The empirical analysis is conducted using daily closing prices and realized measures from 2000 to 2022 across 31 market indices. The proposed models one step ahead VaR forecasting performance is compared against a basic HAR model and its extensions. The results demonstrate that the proposed RNN-HAR model consistently outperforms all other models considered in the study.

DeepVol: A Deep Transfer Learning Approach for Universal Asset Volatility Modeling

This paper introduces DeepVol, a promising new deep learning volatility model that outperforms traditional econometric models in terms of model generality. DeepVol leverages the power of transfer learning to effectively capture and model the volatility dynamics of all financial assets, including previously unseen ones, using a single universal model. This contrasts to the prevailing practice in econometrics literature, which necessitates training separate models for individual datasets. The introduction of DeepVol opens up new avenues for volatility modeling and forecasting in the finance industry, potentially transforming the way volatility is understood and predicted.

A Bayesian Long Short-Term Memory Model for Value at Risk and Expected Shortfall Joint Forecasting

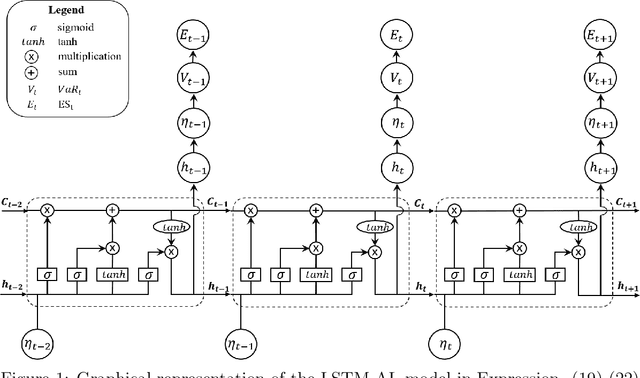
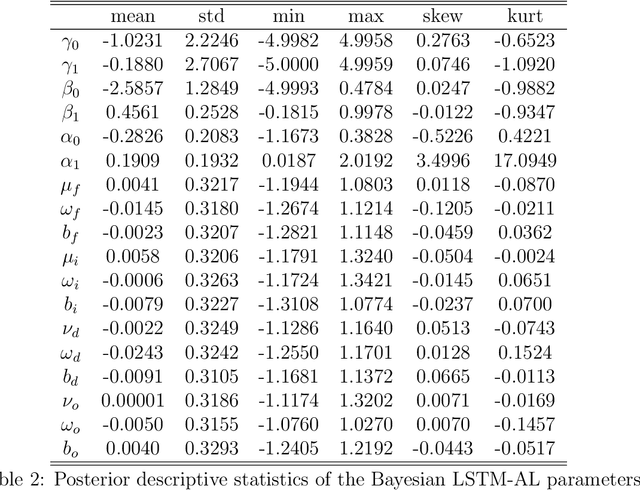
Value-at-Risk (VaR) and Expected Shortfall (ES) are widely used in the financial sector to measure the market risk and manage the extreme market movement. The recent link between the quantile score function and the Asymmetric Laplace density has led to a flexible likelihood-based framework for joint modelling of VaR and ES. It is of high interest in financial applications to be able to capture the underlying joint dynamics of these two quantities. We address this problem by developing a hybrid model that is based on the Asymmetric Laplace quasi-likelihood and employs the Long Short-Term Memory (LSTM) time series modelling technique from Machine Learning to capture efficiently the underlying dynamics of VaR and ES. We refer to this model as LSTM-AL. We adopt the adaptive Markov chain Monte Carlo (MCMC) algorithm for Bayesian inference in the LSTM-AL model. Empirical results show that the proposed LSTM-AL model can improve the VaR and ES forecasting accuracy over a range of well-established competing models.

Manifold Optimisation Assisted Gaussian Variational Approximation

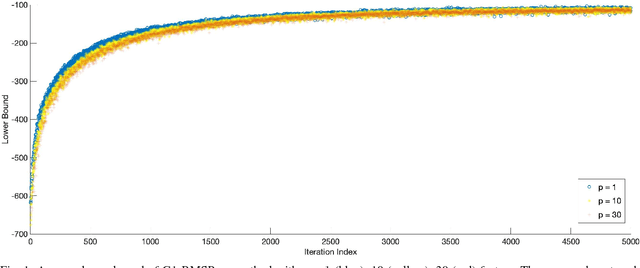
Variational approximation methods are a way to approximate the posterior in Bayesian inference especially when the dataset has a large volume or high dimension. Factor covariance structure was introduced in previous work with three restrictions to handle the problem of computational infeasibility in Gaussian approximation. However, the three strong constraints on the covariance matrix could possibly break down during the process of the structure optimization, and the identification issue could still possibly exist within the final approximation. In this paper, we consider two types of manifold parameterization, Stiefel manifold and Grassmann manifold, to address the problems. Moreover, the Riemannian stochastic gradient descent method is applied to solve the resulting optimization problem while maintaining the orthogonal factors. Results from two experiments demonstrate that our model fixes the potential issue of the previous method with comparable accuracy and competitive converge speed even in high-dimensional problems.

Bayesian Nonparametric Adaptive Spectral Density Estimation for Financial Time Series

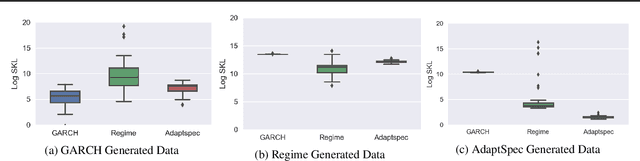
Discrimination between non-stationarity and long-range dependency is a difficult and long-standing issue in modelling financial time series. This paper uses an adaptive spectral technique which jointly models the non-stationarity and dependency of financial time series in a non-parametric fashion assuming that the time series consists of a finite, but unknown number, of locally stationary processes, the locations of which are also unknown. The model allows a non-parametric estimate of the dependency structure by modelling the auto-covariance function in the spectral domain. All our estimates are made within a Bayesian framework where we use aReversible Jump Markov Chain Monte Carlo algorithm for inference. We study the frequentist properties of our estimates via a simulation study, and present a novel way of generating time series data from a nonparametric spectrum. Results indicate that our techniques perform well across a range of data generating processes. We apply our method to a number of real examples and our results indicate that several financial time series exhibit both long-range dependency and non-stationarity.

Fighting Accounting Fraud Through Forensic Data Analytics

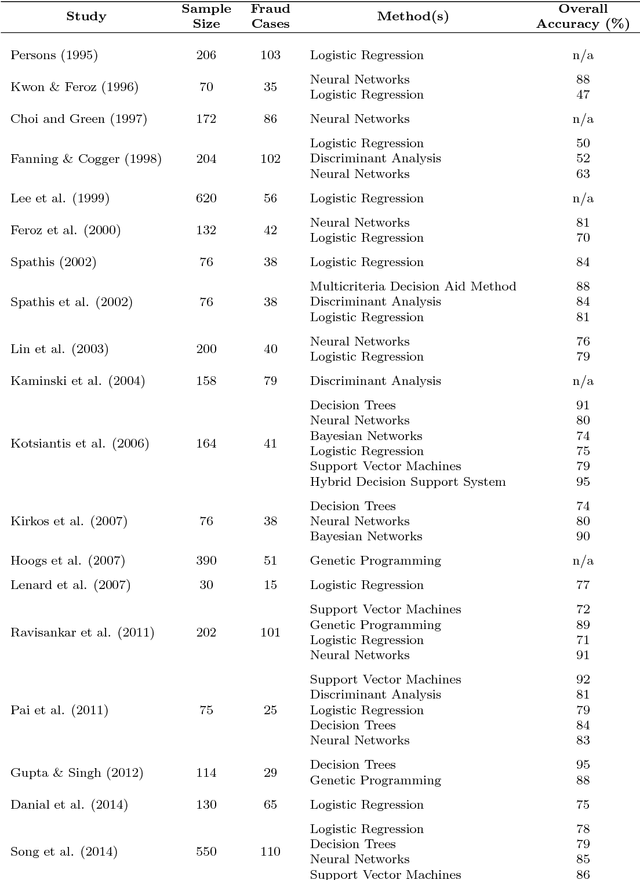
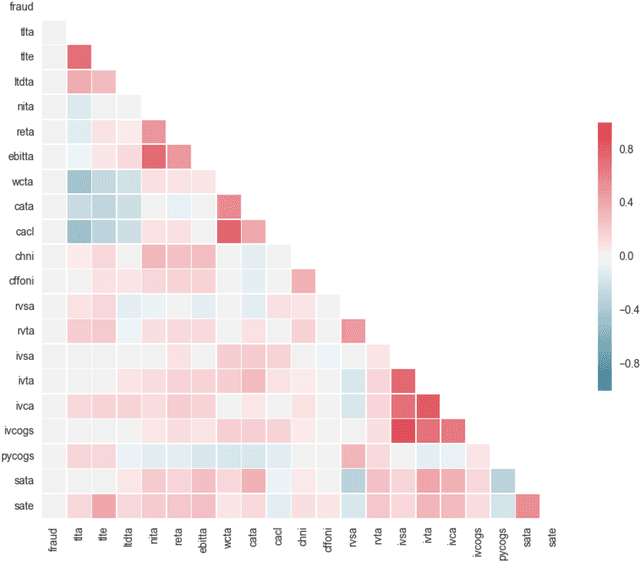
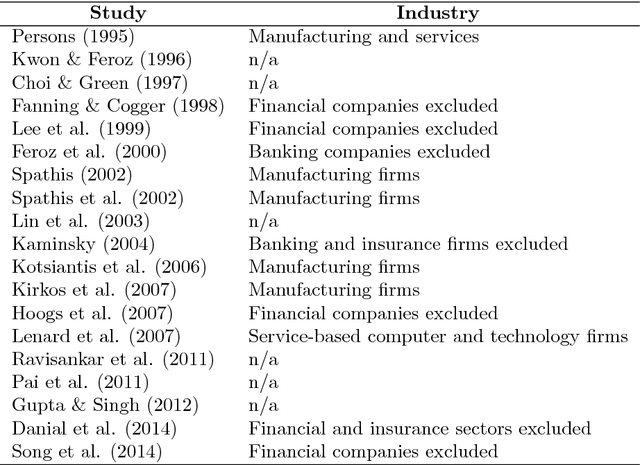
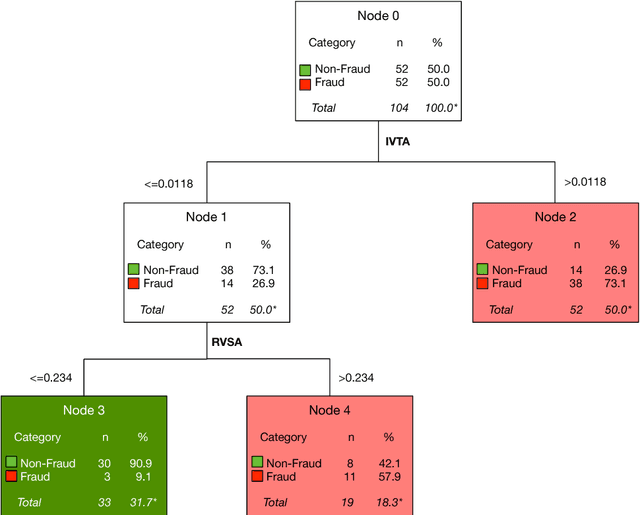
Accounting fraud is a global concern representing a significant threat to the financial system stability due to the resulting diminishing of the market confidence and trust of regulatory authorities. Several tricks can be used to commit accounting fraud, hence the need for non-static regulatory interventions that take into account different fraudulent patterns. Accordingly, this study aims to improve the detection of accounting fraud via the implementation of several machine learning methods to better differentiate between fraud and non-fraud companies, and to further assist the task of examination within the riskier firms by evaluating relevant financial indicators. Out-of-sample results suggest there is a great potential in detecting falsified financial statements through statistical modelling and analysis of publicly available accounting information. The proposed methodology can be of assistance to public auditors and regulatory agencies as it facilitates auditing processes, and supports more targeted and effective examinations of accounting reports.