Covariate Dependent Mixture of Bayesian Networks

Learning the structure of Bayesian networks from data provides insights into underlying processes and the causal relationships that generate the data, but its usefulness depends on the homogeneity of the data population, a condition often violated in real-world applications. In such cases, using a single network structure for inference can be misleading, as it may not capture sub-population differences. To address this, we propose a novel approach of modelling a mixture of Bayesian networks where component probabilities depend on individual characteristics. Our method identifies both network structures and demographic predictors of sub-population membership, aiding personalised interventions. We evaluate our method through simulations and a youth mental health case study, demonstrating its potential to improve tailored interventions in health, education, and social policy.

Bayesian Nonparametric Adaptive Spectral Density Estimation for Financial Time Series

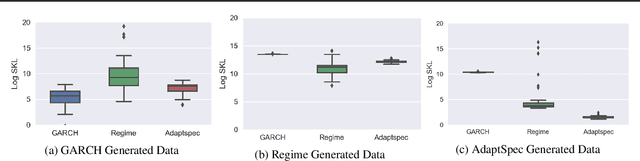
Discrimination between non-stationarity and long-range dependency is a difficult and long-standing issue in modelling financial time series. This paper uses an adaptive spectral technique which jointly models the non-stationarity and dependency of financial time series in a non-parametric fashion assuming that the time series consists of a finite, but unknown number, of locally stationary processes, the locations of which are also unknown. The model allows a non-parametric estimate of the dependency structure by modelling the auto-covariance function in the spectral domain. All our estimates are made within a Bayesian framework where we use aReversible Jump Markov Chain Monte Carlo algorithm for inference. We study the frequentist properties of our estimates via a simulation study, and present a novel way of generating time series data from a nonparametric spectrum. Results indicate that our techniques perform well across a range of data generating processes. We apply our method to a number of real examples and our results indicate that several financial time series exhibit both long-range dependency and non-stationarity.

Sequential Bayesian Optimisation as a POMDP for Environment Monitoring with UAVs

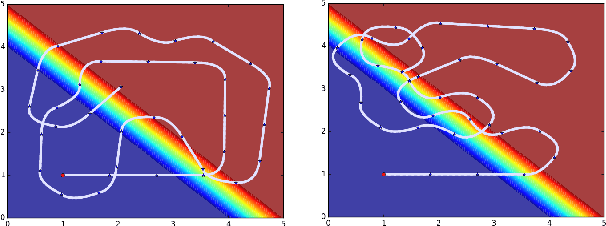
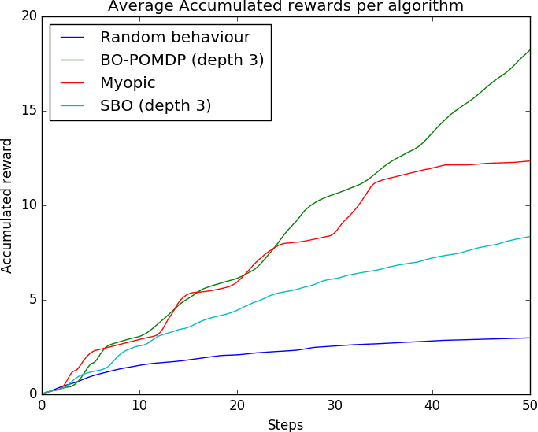
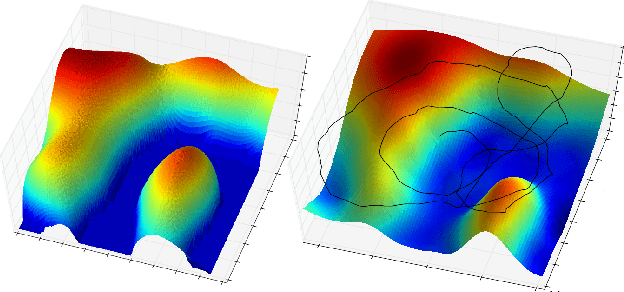
Bayesian Optimisation has gained much popularity lately, as a global optimisation technique for functions that are expensive to evaluate or unknown a priori. While classical BO focuses on where to gather an observation next, it does not take into account practical constraints for a robotic system such as where it is physically possible to gather samples from, nor the sequential nature of the problem while executing a trajectory. In field robotics and other real-life situations, physical and trajectory constraints are inherent problems. This paper addresses these issues by formulating Bayesian Optimisation for continuous trajectories within a Partially Observable Markov Decision Process (POMDP) framework. The resulting POMDP is solved using Monte-Carlo Tree Search (MCTS), which we adapt to using a reward function balancing exploration and exploitation. Experiments on monitoring a spatial phenomenon with a UAV illustrate how our BO-POMDP algorithm outperforms competing techniques.

Occupancy Map Building through Bayesian Exploration

We propose a novel holistic approach for safe autonomous exploration and map building based on constrained Bayesian optimisation. This method finds optimal continuous paths instead of discrete sensing locations that inherently satisfy motion and safety constraints. Evaluating both the objective and constraints functions requires forward simulation of expected observations. As such evaluations are costly, the Bayesian optimiser proposes only paths which are likely to yield optimal results and satisfy the constraints with high confidence. By balancing the reward and risk associated with each path, the optimiser minimises the number of expensive function evaluations. We demonstrate the effectiveness of our approach in a series of experiments both in simulation and with a real ground robot and provide comparisons to other exploration techniques. Evidently, each method has its specific favourable conditions, where it outperforms all other techniques. Yet, by reasoning on the usefulness of the entire path instead of its end point, our method provides a robust and consistent performance through all tests and performs better than or as good as the other leading methods.