Optimal Particle-based Approximation of Discrete Distributions (OPAD)

Particle-based methods include a variety of techniques, such as Markov Chain Monte Carlo (MCMC) and Sequential Monte Carlo (SMC), for approximating a probabilistic target distribution with a set of weighted particles. In this paper, we prove that for any set of particles, there is a unique weighting mechanism that minimizes the Kullback-Leibler (KL) divergence of the (particle-based) approximation from the target distribution, when that distribution is discrete -- any other weighting mechanism (e.g. MCMC weighting that is based on particles' repetitions in the Markov chain) is sub-optimal with respect to this divergence measure. Our proof does not require any restrictions either on the target distribution, or the process by which the particles are generated, other than the discreteness of the target. We show that the optimal weights can be determined based on values that any existing particle-based method already computes; As such, with minimal modifications and no extra computational costs, the performance of any particle-based method can be improved. Our empirical evaluations are carried out on important applications of discrete distributions including Bayesian Variable Selection and Bayesian Structure Learning. The results illustrate that our proposed reweighting of the particles improves any particle-based approximation to the target distribution consistently and often substantially.

Distilled Reverse Attention Network for Open-world Compositional Zero-Shot Learning

Open-World Compositional Zero-Shot Learning (OW-CZSL) aims to recognize new compositions of seen attributes and objects. In OW-CZSL, methods built on the conventional closed-world setting degrade severely due to the unconstrained OW test space. While previous works alleviate the issue by pruning compositions according to external knowledge or correlations in seen pairs, they introduce biases that harm the generalization. Some methods thus predict state and object with independently constructed and trained classifiers, ignoring that attributes are highly context-dependent and visually entangled with objects. In this paper, we propose a novel Distilled Reverse Attention Network to address the challenges. We also model attributes and objects separately but with different motivations, capturing contextuality and locality, respectively. We further design a reverse-and-distill strategy that learns disentangled representations of elementary components in training data supervised by reverse attention and knowledge distillation. We conduct experiments on three datasets and consistently achieve state-of-the-art (SOTA) performance.

Structured Variational Inference in Continuous Cox Process Models

We propose a scalable framework for inference in an inhomogeneous Poisson process modeled by a continuous sigmoidal Cox process that assumes the corresponding intensity function is given by a Gaussian process (GP) prior transformed with a scaled logistic sigmoid function. We present a tractable representation of the likelihood through augmentation with a superposition of Poisson processes. This view enables a structured variational approximation capturing dependencies across variables in the model. Our framework avoids discretization of the domain, does not require accurate numerical integration over the input space and is not limited to GPs with squared exponential kernels. We evaluate our approach on synthetic and real-world data showing that its benefits are particularly pronounced on multivariate input settings where it overcomes the limitations of mean-field methods and sampling schemes. We provide the state of-the-art in terms of speed, accuracy and uncertainty quantification trade-offs.

Bayesian Nonparametric Adaptive Spectral Density Estimation for Financial Time Series

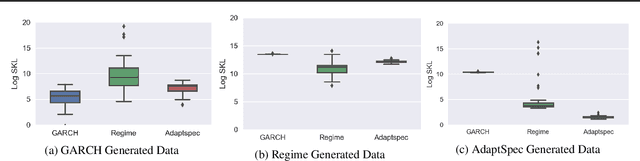
Discrimination between non-stationarity and long-range dependency is a difficult and long-standing issue in modelling financial time series. This paper uses an adaptive spectral technique which jointly models the non-stationarity and dependency of financial time series in a non-parametric fashion assuming that the time series consists of a finite, but unknown number, of locally stationary processes, the locations of which are also unknown. The model allows a non-parametric estimate of the dependency structure by modelling the auto-covariance function in the spectral domain. All our estimates are made within a Bayesian framework where we use aReversible Jump Markov Chain Monte Carlo algorithm for inference. We study the frequentist properties of our estimates via a simulation study, and present a novel way of generating time series data from a nonparametric spectrum. Results indicate that our techniques perform well across a range of data generating processes. We apply our method to a number of real examples and our results indicate that several financial time series exhibit both long-range dependency and non-stationarity.

Efficiency and robustness in Monte Carlo sampling of 3-D geophysical inversions with Obsidian v0.1.2: Setting up for success

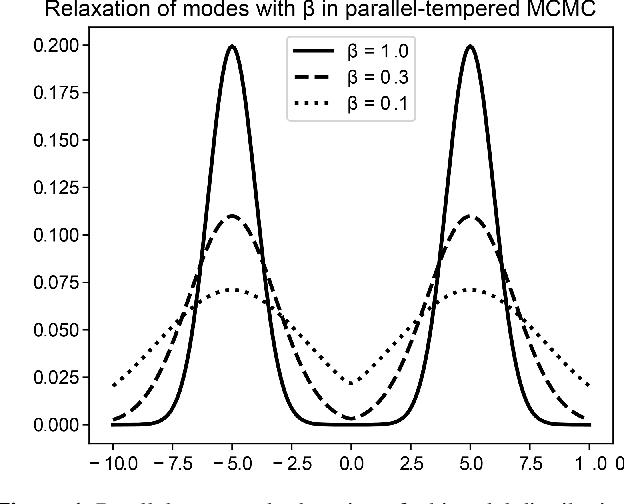
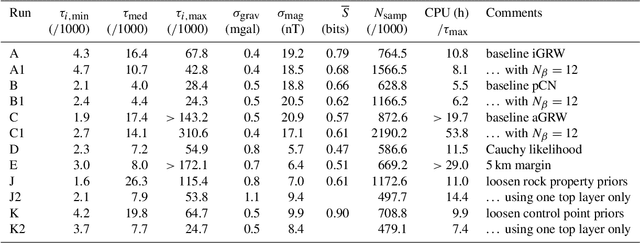
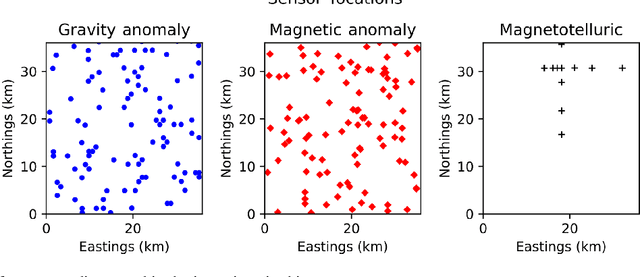
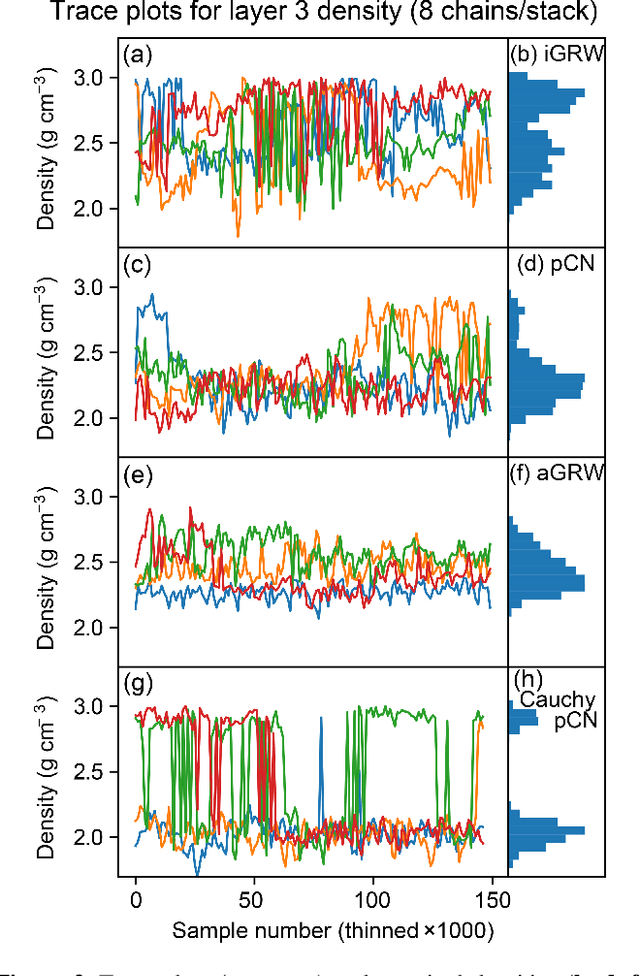
The rigorous quantification of uncertainty in geophysical inversions is a challenging problem. Inversions are often ill-posed and the likelihood surface may be multi-modal; properties of any single mode become inadequate uncertainty measures, and sampling methods become inefficient for irregular posteriors or high-dimensional parameter spaces. We explore the influences of different choices made by the practitioner on the efficiency and accuracy of Bayesian geophysical inversion methods that rely on Markov chain Monte Carlo sampling to assess uncertainty, using a multi-sensor inversion of the three-dimensional structure and composition of a region in the Cooper Basin of South Australia as a case study. The inversion is performed using an updated version of the Obsidian distributed inversion software. We find that the posterior for this inversion has complex local covariance structure, hindering the efficiency of adaptive sampling methods that adjust the proposal based on the chain history. Within the context of a parallel-tempered Markov chain Monte Carlo scheme for exploring high-dimensional multi-modal posteriors, a preconditioned Crank-Nicholson proposal outperforms more conventional forms of random walk. Aspects of the problem setup, such as priors on petrophysics or on 3-D geological structure, affect the shape and separation of posterior modes, influencing sampling performance as well as the inversion results. Use of uninformative priors on sensor noise can improve inversion results by enabling optimal weighting among multiple sensors even if noise levels are uncertain. Efficiency could be further increased by using posterior gradient information within proposals, which Obsidian does not currently support, but which could be emulated using posterior surrogates.

Langevin-gradient parallel tempering for Bayesian neural learning

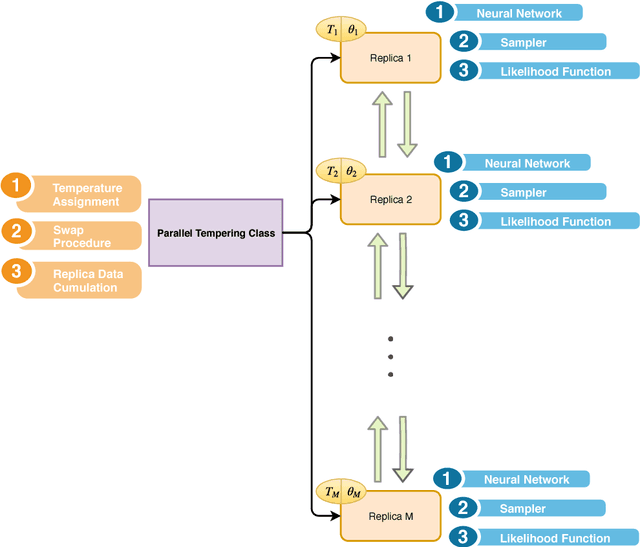
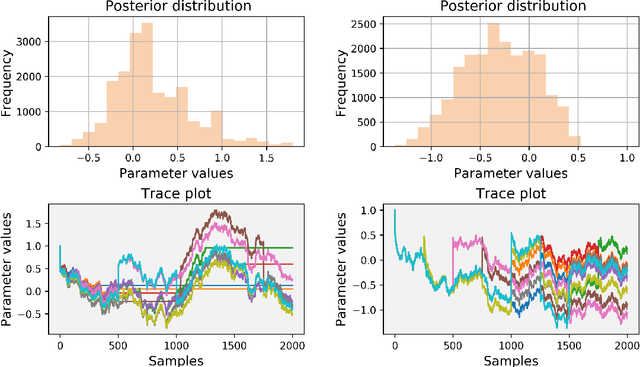
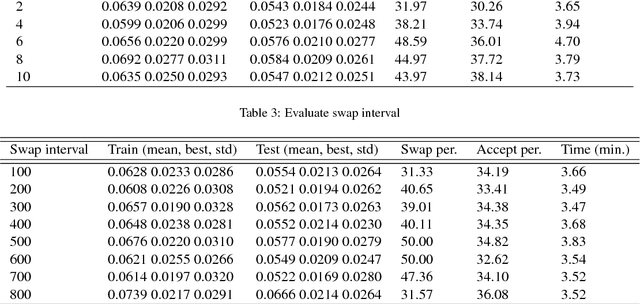
Bayesian neural learning feature a rigorous approach to estimation and uncertainty quantification via the posterior distribution of weights that represent knowledge of the neural network. This not only provides point estimates of optimal set of weights but also the ability to quantify uncertainty in decision making using the posterior distribution. Markov chain Monte Carlo (MCMC) techniques are typically used to obtain sample-based estimates of the posterior distribution. However, these techniques face challenges in convergence and scalability, particularly in settings with large datasets and network architectures. This paper address these challenges in two ways. First, parallel tempering is used used to explore multiple modes of the posterior distribution and implemented in multi-core computing architecture. Second, we make within-chain sampling schemes more efficient by using Langevin gradient information in forming Metropolis-Hastings proposal distributions. We demonstrate the techniques using time series prediction and pattern classification applications. The results show that the method not only improves the computational time, but provides better prediction or decision making capabilities when compared to related methods.

BayesLands: A Bayesian inference approach for parameter uncertainty quantification in Badlands

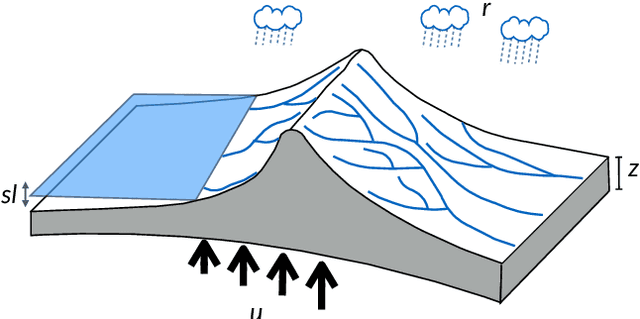
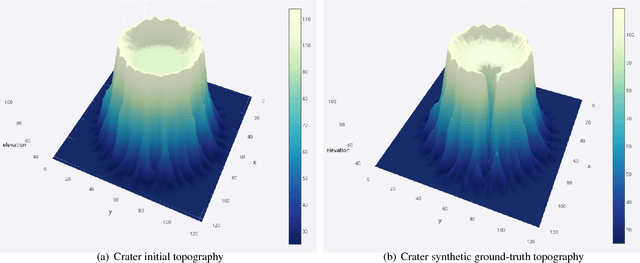
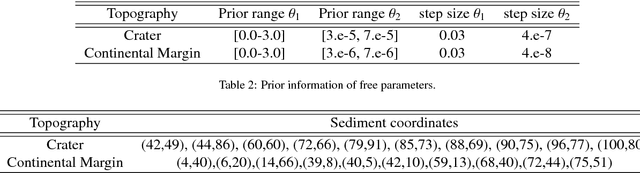
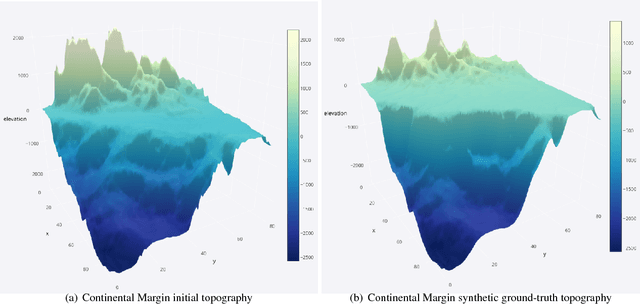
Bayesian inference provides a principled approach towards uncertainty quantification of free parameters in geophysical forward models. This provides advantages over optimization methods that provide single point estimates as solutions, which lack uncertainty quantification. Badlands (basin and landscape dynamics model) is geophysical forward model that simulates topography development at various space and time scales. Badlands consists of a number of geophysical parameters that need to be estimated with appropriate uncertainty quantification, given the observed ground truth such as surface topography, sediment thickness and stratigraphy through time. This is challenging due to the scarcity of data, sensitivity of the parameters and complexity of the Badlands model. In this paper, we take a Bayesian approach to provide inference using Markov chain Monte Carlo sampling (MCMC). Hence, we present \textit{BayesLands}, a Bayesian framework for Badlands that fuses information obtained from complex forward models with observational data and prior knowledge. As a proof-of-concept, we consider a synthetic and real-world topography with two free parameters, namely precipitation and erodibility, that we need to estimate through BayesLands. The results of the experiments shows that BayesLands yields a promising distribution of the parameters. Moreover, the challenge in sampling due to multi-modality is presented through visualizing a likelihood surface that has a range of suboptimal modes.