R. Dietmar Müller
Surrogate-assisted Bayesian inversion for landscape and basin evolution models
Dec 12, 2018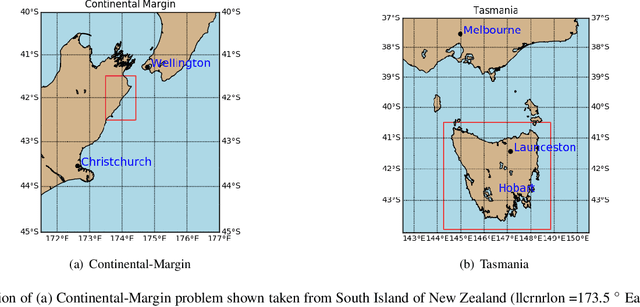
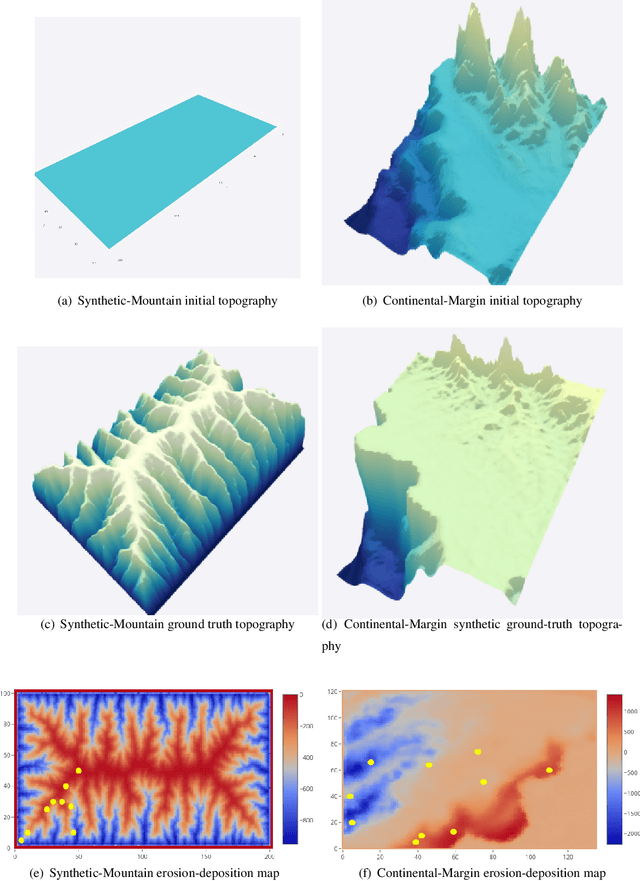

Abstract:The complex and computationally expensive features of the forward landscape and sedimentary basin evolution models pose a major challenge in the development of efficient inference and optimization methods. Bayesian inference provides a methodology for estimation and uncertainty quantification of free model parameters. In our previous work, parallel tempering Bayeslands was developed as a framework for parameter estimation and uncertainty quantification for the landscape and basin evolution modelling software Badlands. Parallel tempering Bayeslands features high-performance computing with dozens of processing cores running in parallel to enhance computational efficiency. Although parallel computing is used, the procedure remains computationally challenging since thousands of samples need to be drawn and evaluated. In large-scale landscape and basin evolution problems, a single model evaluation can take from several minutes to hours, and in certain cases, even days. Surrogate-assisted optimization has been with successfully applied to a number of engineering problems. This motivates its use in optimisation and inference methods suited for complex models in geology and geophysics. Surrogates can speed up parallel tempering Bayeslands by developing computationally inexpensive surrogates to mimic expensive models. In this paper, we present an application of surrogate-assisted parallel tempering where that surrogate mimics a landscape evolution model including erosion, sediment transport and deposition, by estimating the likelihood function that is given by the model. We employ a machine learning model as a surrogate that learns from the samples generated by the parallel tempering algorithm. The results show that the methodology is effective in lowering the overall computational cost significantly while retaining the quality of solutions.
BayesLands: A Bayesian inference approach for parameter uncertainty quantification in Badlands
May 02, 2018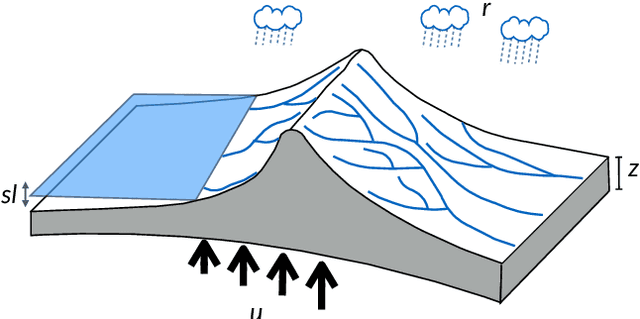
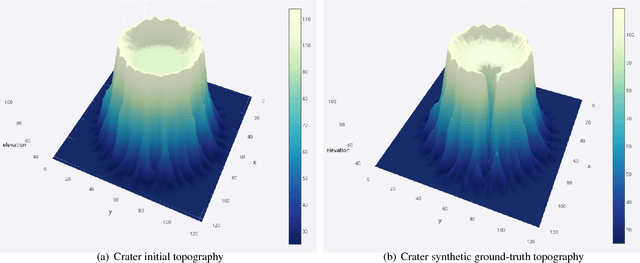
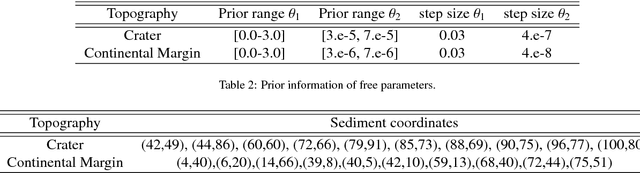
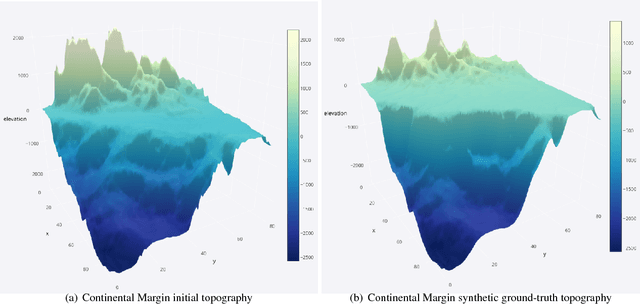
Abstract:Bayesian inference provides a principled approach towards uncertainty quantification of free parameters in geophysical forward models. This provides advantages over optimization methods that provide single point estimates as solutions, which lack uncertainty quantification. Badlands (basin and landscape dynamics model) is geophysical forward model that simulates topography development at various space and time scales. Badlands consists of a number of geophysical parameters that need to be estimated with appropriate uncertainty quantification, given the observed ground truth such as surface topography, sediment thickness and stratigraphy through time. This is challenging due to the scarcity of data, sensitivity of the parameters and complexity of the Badlands model. In this paper, we take a Bayesian approach to provide inference using Markov chain Monte Carlo sampling (MCMC). Hence, we present \textit{BayesLands}, a Bayesian framework for Badlands that fuses information obtained from complex forward models with observational data and prior knowledge. As a proof-of-concept, we consider a synthetic and real-world topography with two free parameters, namely precipitation and erodibility, that we need to estimate through BayesLands. The results of the experiments shows that BayesLands yields a promising distribution of the parameters. Moreover, the challenge in sampling due to multi-modality is presented through visualizing a likelihood surface that has a range of suboptimal modes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge