BayesLands: A Bayesian inference approach for parameter uncertainty quantification in Badlands

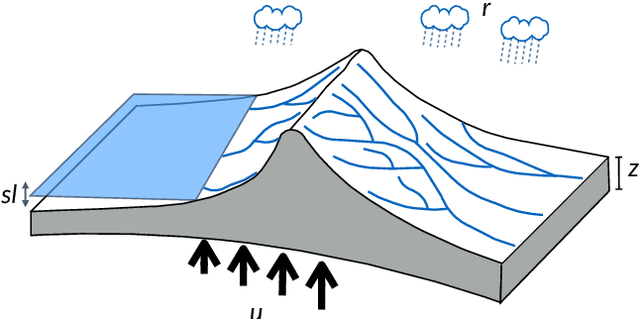
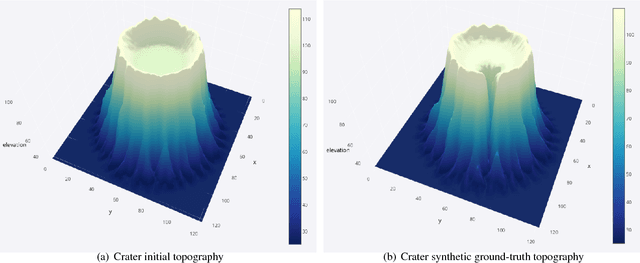
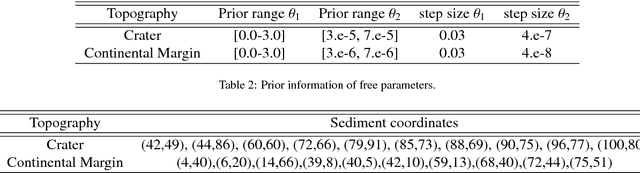
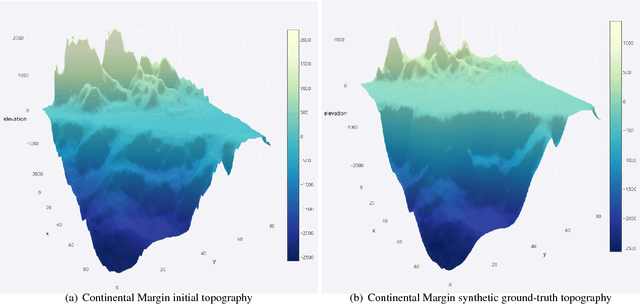
Bayesian inference provides a principled approach towards uncertainty quantification of free parameters in geophysical forward models. This provides advantages over optimization methods that provide single point estimates as solutions, which lack uncertainty quantification. Badlands (basin and landscape dynamics model) is geophysical forward model that simulates topography development at various space and time scales. Badlands consists of a number of geophysical parameters that need to be estimated with appropriate uncertainty quantification, given the observed ground truth such as surface topography, sediment thickness and stratigraphy through time. This is challenging due to the scarcity of data, sensitivity of the parameters and complexity of the Badlands model. In this paper, we take a Bayesian approach to provide inference using Markov chain Monte Carlo sampling (MCMC). Hence, we present \textit{BayesLands}, a Bayesian framework for Badlands that fuses information obtained from complex forward models with observational data and prior knowledge. As a proof-of-concept, we consider a synthetic and real-world topography with two free parameters, namely precipitation and erodibility, that we need to estimate through BayesLands. The results of the experiments shows that BayesLands yields a promising distribution of the parameters. Moreover, the challenge in sampling due to multi-modality is presented through visualizing a likelihood surface that has a range of suboptimal modes.