When AI Trading Agents Compete: Adverse Selection of Meta-Orders by Reinforcement Learning-Based Market Making

We investigate the mechanisms by which medium-frequency trading agents are adversely selected by opportunistic high-frequency traders. We use reinforcement learning (RL) within a Hawkes Limit Order Book (LOB) model in order to replicate the behaviours of high-frequency market makers. In contrast to the classical models with exogenous price impact assumptions, the Hawkes model accounts for endogenous price impact and other key properties of the market (Jain et al. 2024a). Given the real-world impracticalities of the market maker updating strategies for every event in the LOB, we formulate the high-frequency market making agent via an impulse control reinforcement learning framework (Jain et al. 2025). The RL used in the simulation utilises Proximal Policy Optimisation (PPO) and self-imitation learning. To replicate the adverse selection phenomenon, we test the RL agent trading against a medium frequency trader (MFT) executing a meta-order and demonstrate that, with training against the MFT meta-order execution agent, the RL market making agent learns to capitalise on the price drift induced by the meta-order. Recent empirical studies have shown that medium-frequency traders are increasingly subject to adverse selection by high-frequency trading agents. As high-frequency trading continues to proliferate across financial markets, the slippage costs incurred by medium-frequency traders are likely to increase over time. However, we do not observe that increased profits for the market making RL agent necessarily cause significantly increased slippages for the MFT agent.

Surrogate-assisted parallel tempering for Bayesian neural learning

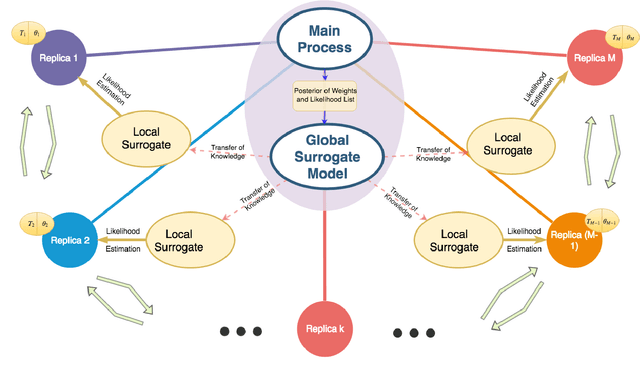
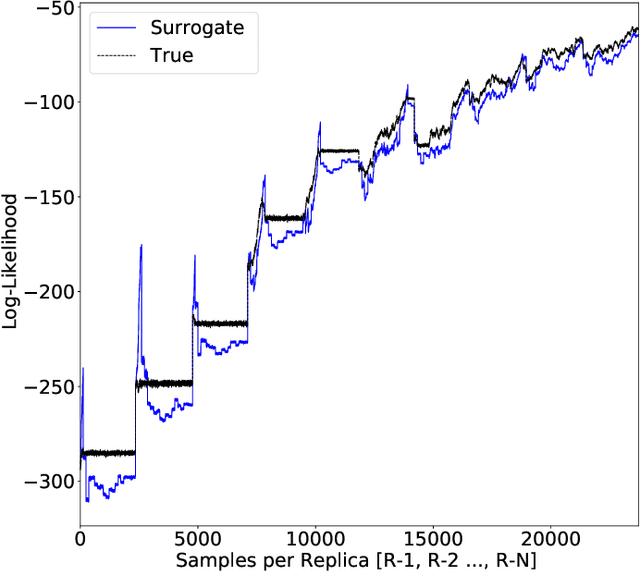
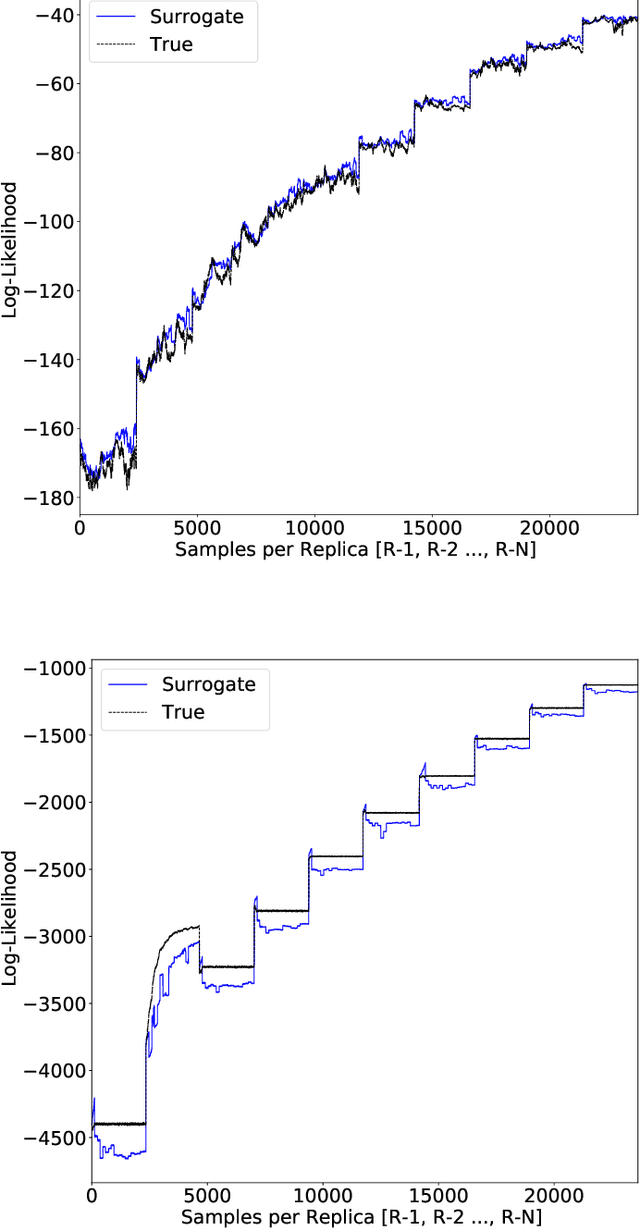
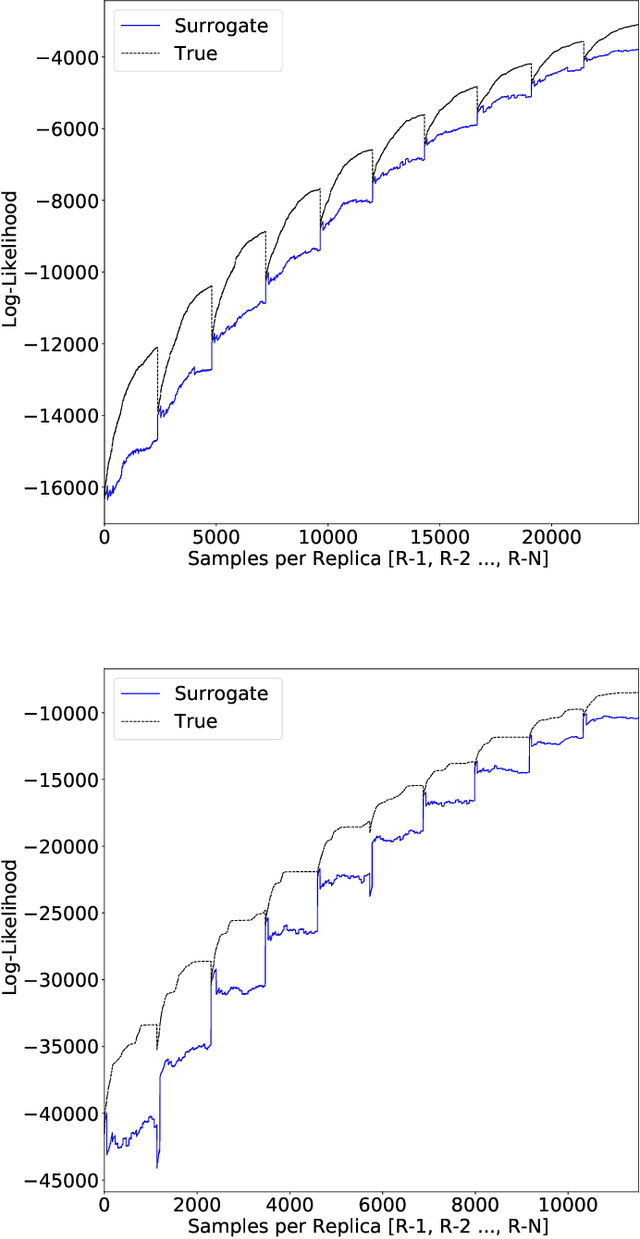
Parallel tempering addresses some of the drawbacks of canonical Markov Chain Monte-Carlo methods for Bayesian neural learning with the ability to utilize high performance computing. However, certain challenges remain given the large range of network parameters and big data. Surrogate-assisted optimization considers the estimation of an objective function for models given computational inefficiency or difficulty to obtain clear results. We address the inefficiency of parallel tempering for large-scale problems by combining parallel computing features with surrogate assisted estimation of likelihood function that describes the plausibility of a model parameter value, given specific observed data. In this paper, we present surrogate-assisted parallel tempering for Bayesian neural learning where the surrogates are used to estimate the likelihood. The estimation via the surrogate becomes useful rather than evaluating computationally expensive models that feature large number of parameters and datasets. Our results demonstrate that the methodology significantly lowers the computational cost while maintaining quality in decision making using Bayesian neural learning. The method has applications for a Bayesian inversion and uncertainty quantification for a broad range of numerical models.

Langevin-gradient parallel tempering for Bayesian neural learning

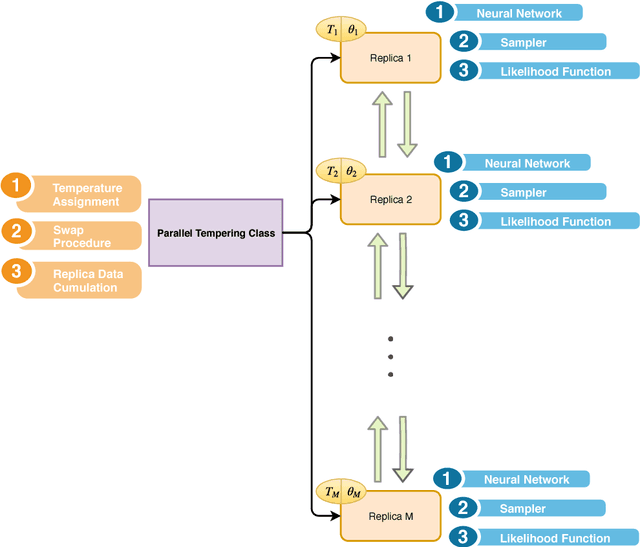
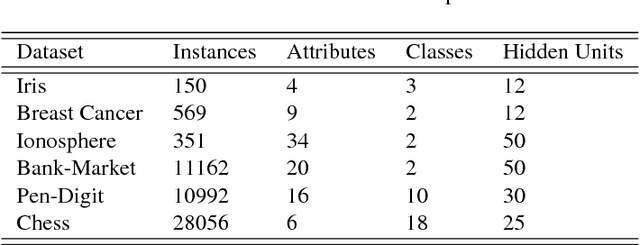
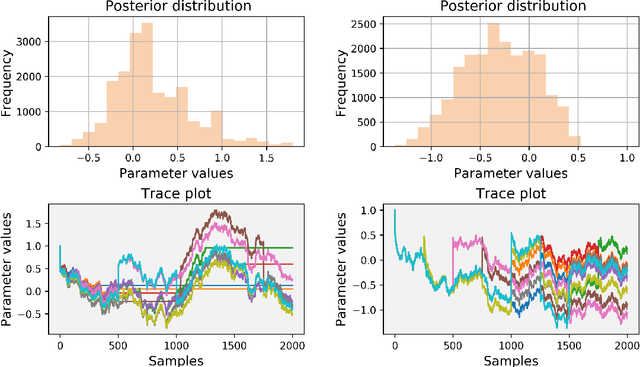
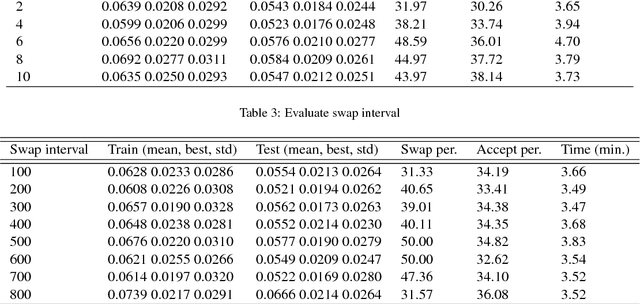
Bayesian neural learning feature a rigorous approach to estimation and uncertainty quantification via the posterior distribution of weights that represent knowledge of the neural network. This not only provides point estimates of optimal set of weights but also the ability to quantify uncertainty in decision making using the posterior distribution. Markov chain Monte Carlo (MCMC) techniques are typically used to obtain sample-based estimates of the posterior distribution. However, these techniques face challenges in convergence and scalability, particularly in settings with large datasets and network architectures. This paper address these challenges in two ways. First, parallel tempering is used used to explore multiple modes of the posterior distribution and implemented in multi-core computing architecture. Second, we make within-chain sampling schemes more efficient by using Langevin gradient information in forming Metropolis-Hastings proposal distributions. We demonstrate the techniques using time series prediction and pattern classification applications. The results show that the method not only improves the computational time, but provides better prediction or decision making capabilities when compared to related methods.