Surrogate-assisted parallel tempering for Bayesian neural learning

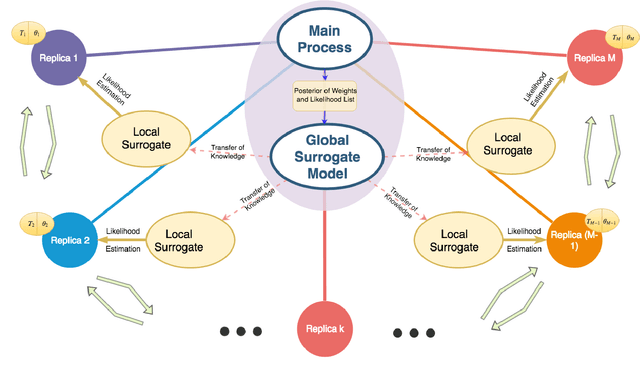
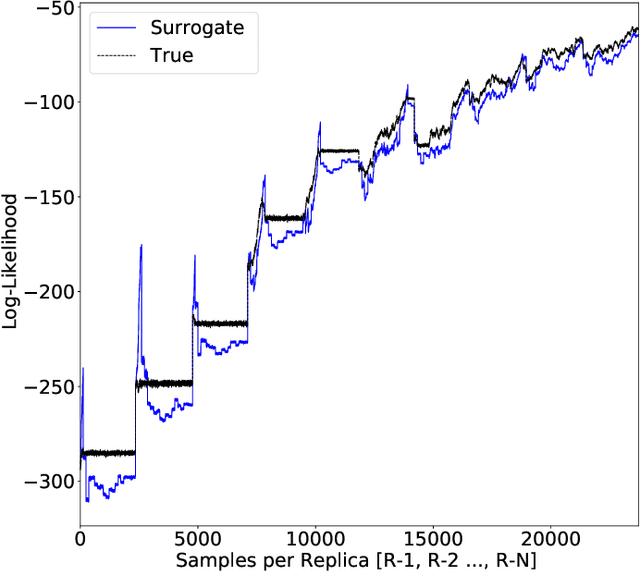
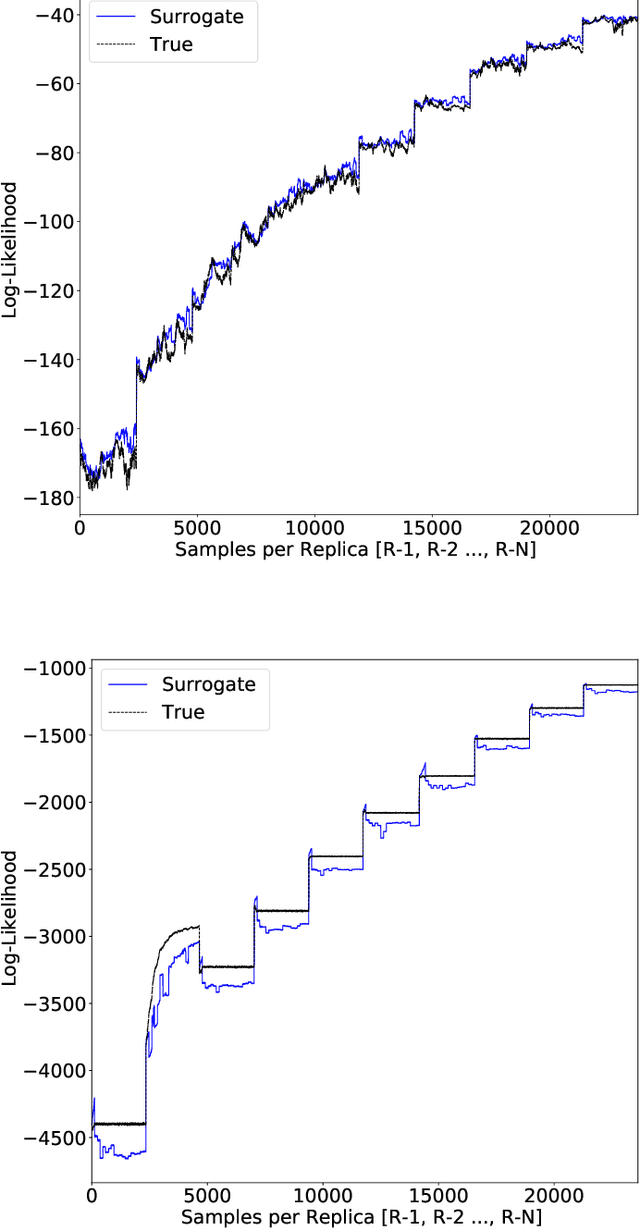
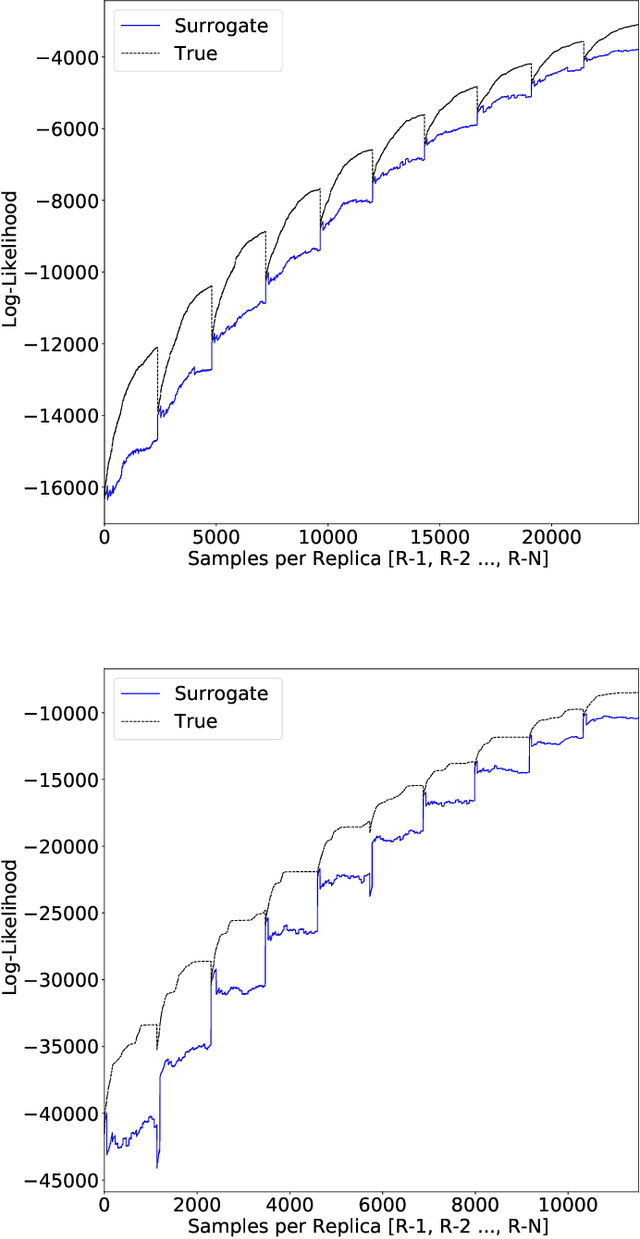
Parallel tempering addresses some of the drawbacks of canonical Markov Chain Monte-Carlo methods for Bayesian neural learning with the ability to utilize high performance computing. However, certain challenges remain given the large range of network parameters and big data. Surrogate-assisted optimization considers the estimation of an objective function for models given computational inefficiency or difficulty to obtain clear results. We address the inefficiency of parallel tempering for large-scale problems by combining parallel computing features with surrogate assisted estimation of likelihood function that describes the plausibility of a model parameter value, given specific observed data. In this paper, we present surrogate-assisted parallel tempering for Bayesian neural learning where the surrogates are used to estimate the likelihood. The estimation via the surrogate becomes useful rather than evaluating computationally expensive models that feature large number of parameters and datasets. Our results demonstrate that the methodology significantly lowers the computational cost while maintaining quality in decision making using Bayesian neural learning. The method has applications for a Bayesian inversion and uncertainty quantification for a broad range of numerical models.