Ratneel V. Deo
Langevin-gradient parallel tempering for Bayesian neural learning
Nov 11, 2018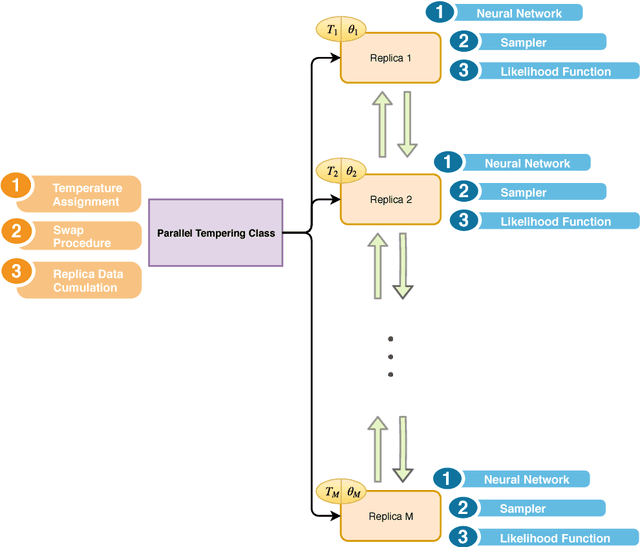
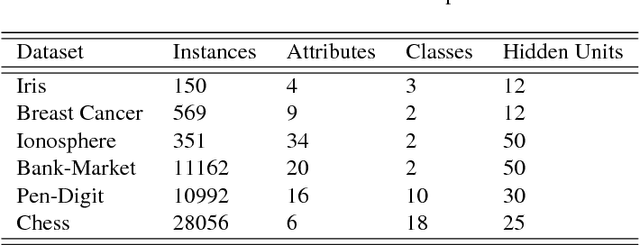
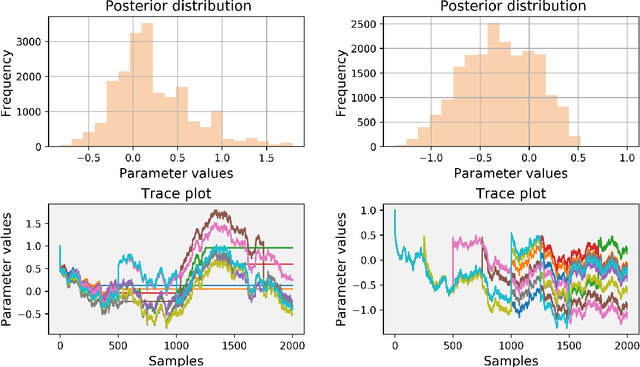
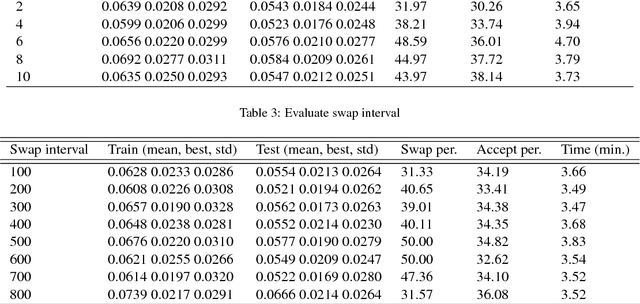
Abstract:Bayesian neural learning feature a rigorous approach to estimation and uncertainty quantification via the posterior distribution of weights that represent knowledge of the neural network. This not only provides point estimates of optimal set of weights but also the ability to quantify uncertainty in decision making using the posterior distribution. Markov chain Monte Carlo (MCMC) techniques are typically used to obtain sample-based estimates of the posterior distribution. However, these techniques face challenges in convergence and scalability, particularly in settings with large datasets and network architectures. This paper address these challenges in two ways. First, parallel tempering is used used to explore multiple modes of the posterior distribution and implemented in multi-core computing architecture. Second, we make within-chain sampling schemes more efficient by using Langevin gradient information in forming Metropolis-Hastings proposal distributions. We demonstrate the techniques using time series prediction and pattern classification applications. The results show that the method not only improves the computational time, but provides better prediction or decision making capabilities when compared to related methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge