Variational Learning of Fractional Posteriors

We introduce a novel one-parameter variational objective that lower bounds the data evidence and enables the estimation of approximate fractional posteriors. We extend this framework to hierarchical construction and Bayes posteriors, offering a versatile tool for probabilistic modelling. We demonstrate two cases where gradients can be obtained analytically and a simulation study on mixture models showing that our fractional posteriors can be used to achieve better calibration compared to posteriors from the conventional variational bound. When applied to variational autoencoders (VAEs), our approach attains higher evidence bounds and enables learning of high-performing approximate Bayes posteriors jointly with fractional posteriors. We show that VAEs trained with fractional posteriors produce decoders that are better aligned for generation from the prior.

Active Flow Matching

Discrete diffusion and flow matching models capture complex, non-additive and non-autoregressive structure in high-dimensional objective landscapes through parallel, iterative refinement. However, their implicit generative nature precludes direct integration with principled variational frameworks for online black-box optimisation, such as variational search distributions (VSD) and conditioning by adaptive sampling (CbAS). We introduce Active Flow Matching (AFM), which reformulates variational objectives to operate on conditional endpoint distributions along the flow, enabling gradient-based steering of flow models toward high-fitness regions while preserving the rigour of VSD and CbAS. We derive forward and reverse Kullback-Leibler (KL) variants using self-normalised importance sampling. Across a suite of online protein and small molecule design tasks, forward-KL AFM consistently performs competitively compared to state-of-the-art baselines, demonstrating effective exploration-exploitation under tight experimental budgets.

Multi-Scale Wavelet Transformers for Operator Learning of Dynamical Systems

Recent years have seen a surge in data-driven surrogates for dynamical systems that can be orders of magnitude faster than numerical solvers. However, many machine learning-based models such as neural operators exhibit spectral bias, attenuating high-frequency components that often encode small-scale structure. This limitation is particularly damaging in applications such as weather forecasting, where misrepresented high frequencies can induce long-horizon instability. To address this issue, we propose multi-scale wavelet transformers (MSWTs), which learn system dynamics in a tokenized wavelet domain. The wavelet transform explicitly separates low- and high-frequency content across scales. MSWTs leverage a wavelet-preserving downsampling scheme that retains high-frequency features and employ wavelet-based attention to capture dependencies across scales and frequency bands. Experiments on chaotic dynamical systems show substantial error reductions and improved long horizon spectral fidelity. On the ERA5 climate reanalysis, MSWTs further reduce climatological bias, demonstrating their effectiveness in a real-world forecasting setting.

Causal Preference Elicitation

We propose causal preference elicitation, a Bayesian framework for expert-in-the-loop causal discovery that actively queries local edge relations to concentrate a posterior over directed acyclic graphs (DAGs). From any black-box observational posterior, we model noisy expert judgments with a three-way likelihood over edge existence and direction. Posterior inference uses a flexible particle approximation, and queries are selected by an efficient expected information gain criterion on the expert's categorical response. Experiments on synthetic graphs, protein signaling data, and a human gene perturbation benchmark show faster posterior concentration and improved recovery of directed effects under tight query budgets.

Ordering-based Causal Discovery via Generalized Score Matching

Learning DAG structures from purely observational data remains a long-standing challenge across scientific domains. An emerging line of research leverages the score of the data distribution to initially identify a topological order of the underlying DAG via leaf node detection and subsequently performs edge pruning for graph recovery. This paper extends the score matching framework for causal discovery, which is originally designated for continuous data, and introduces a novel leaf discriminant criterion based on the discrete score function. Through simulated and real-world experiments, we demonstrate that our theory enables accurate inference of true causal orders from observed discrete data and the identified ordering can significantly boost the accuracy of existing causal discovery baselines on nearly all of the settings.

Improving Uncertainty Quantification in Large Language Models via Semantic Embeddings

Accurately quantifying uncertainty in large language models (LLMs) is crucial for their reliable deployment, especially in high-stakes applications. Current state-of-the-art methods for measuring semantic uncertainty in LLMs rely on strict bidirectional entailment criteria between multiple generated responses and also depend on sequence likelihoods. While effective, these approaches often overestimate uncertainty due to their sensitivity to minor wording differences, additional correct information, and non-important words in the sequence. We propose a novel approach that leverages semantic embeddings to achieve smoother and more robust estimation of semantic uncertainty in LLMs. By capturing semantic similarities without depending on sequence likelihoods, our method inherently reduces any biases introduced by irrelevant words in the answers. Furthermore, we introduce an amortised version of our approach by explicitly modelling semantics as latent variables in a joint probabilistic model. This allows for uncertainty estimation in the embedding space with a single forward pass, significantly reducing computational overhead compared to existing multi-pass methods. Experiments across multiple question-answering datasets and frontier LLMs demonstrate that our embedding-based methods provide more accurate and nuanced uncertainty quantification than traditional approaches.

Variational Search Distributions

We develop variational search distributions (VSD), a method for finding discrete, combinatorial designs of a rare desired class in a batch sequential manner with a fixed experimental budget. We formalize the requirements and desiderata for this problem and formulate a solution via variational inference that fulfill these. In particular, VSD uses off-the-shelf gradient based optimization routines, and can take advantage of scalable predictive models. We show that VSD can outperform existing baseline methods on a set of real sequence-design problems in various biological systems.

Rényi Neural Processes

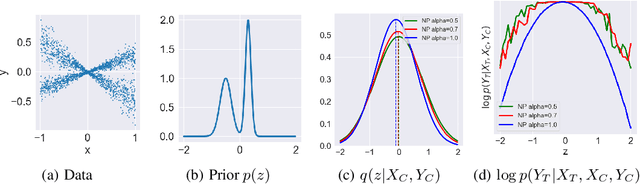
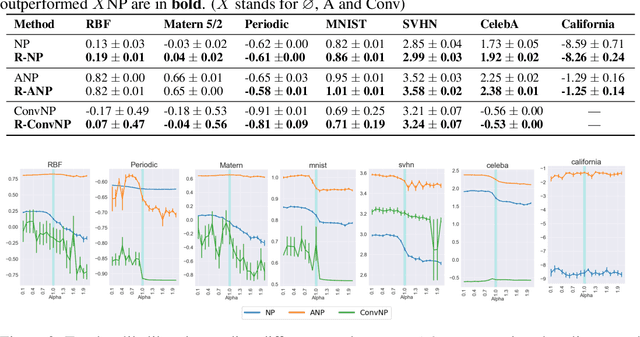
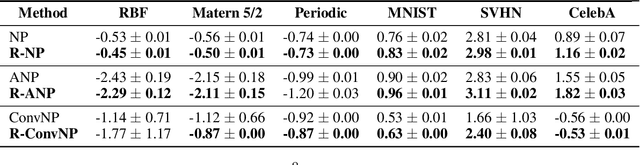
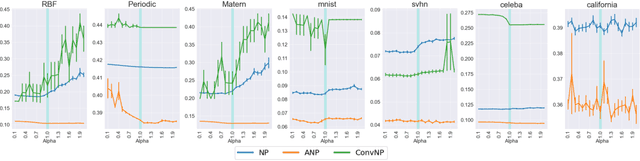
Neural Processes (NPs) are variational frameworks that aim to represent stochastic processes with deep neural networks. Despite their obvious benefits in uncertainty estimation for complex distributions via data-driven priors, NPs enforce network parameter sharing between the conditional prior and posterior distributions, thereby risking introducing a misspecified prior. We hereby propose R\'enyi Neural Processes (RNP) to relax the influence of the misspecified prior and optimize a tighter bound of the marginal likelihood. More specifically, by replacing the standard KL divergence with the R\'enyi divergence between the posterior and the approximated prior, we ameliorate the impact of the misspecified prior via a parameter {\alpha} so that the resulting posterior focuses more on tail samples and reduce density on overconfident regions. Our experiments showed log-likelihood improvements on several existing NP families. We demonstrated the superior performance of our approach on various benchmarks including regression and image inpainting tasks. We also validate the effectiveness of RNPs on real-world tabular regression problems.

ProDAG: Projection-induced variational inference for directed acyclic graphs

Directed acyclic graph (DAG) learning is a rapidly expanding field of research. Though the field has witnessed remarkable advances over the past few years, it remains statistically and computationally challenging to learn a single (point estimate) DAG from data, let alone provide uncertainty quantification. Our article addresses the difficult task of quantifying graph uncertainty by developing a variational Bayes inference framework based on novel distributions that have support directly on the space of DAGs. The distributions, which we use to form our prior and variational posterior, are induced by a projection operation, whereby an arbitrary continuous distribution is projected onto the space of sparse weighted acyclic adjacency matrices (matrix representations of DAGs) with probability mass on exact zeros. Though the projection constitutes a combinatorial optimization problem, it is solvable at scale via recently developed techniques that reformulate acyclicity as a continuous constraint. We empirically demonstrate that our method, ProDAG, can deliver accurate inference, and often outperforms existing state-of-the-art alternatives.

Optimal Transport for Structure Learning Under Missing Data

Causal discovery in the presence of missing data introduces a chicken-and-egg dilemma. While the goal is to recover the true causal structure, robust imputation requires considering the dependencies or preferably causal relations among variables. Merely filling in missing values with existing imputation methods and subsequently applying structure learning on the complete data is empirical shown to be sub-optimal. To this end, we propose in this paper a score-based algorithm, based on optimal transport, for learning causal structure from missing data. This optimal transport viewpoint diverges from existing score-based approaches that are dominantly based on EM. We project structure learning as a density fitting problem, where the goal is to find the causal model that induces a distribution of minimum Wasserstein distance with the distribution over the observed data. Through extensive simulations and real-data experiments, our framework is shown to recover the true causal graphs more effectively than the baselines in various simulations and real-data experiments. Empirical evidences also demonstrate the superior scalability of our approach, along with the flexibility to incorporate any off-the-shelf causal discovery methods for complete data.