Nested AutoRegressive Models

AutoRegressive (AR) models have demonstrated competitive performance in image generation, achieving results comparable to those of diffusion models. However, their token-by-token image generation mechanism remains computationally intensive and existing solutions such as VAR often lead to limited sample diversity. In this work, we propose a Nested AutoRegressive~(NestAR) model, which proposes nested AutoRegressive architectures in generating images. NestAR designs multi-scale modules in a hierarchical order. These different scaled modules are constructed in an AR architecture, where one larger-scale module is conditioned on outputs from its previous smaller-scale module. Within each module, NestAR uses another AR structure to generate ``patches'' of tokens. The proposed nested AR architecture reduces the overall complexity from $\mathcal{O}(n)$ to $\mathcal{O}(\log n)$ in generating $n$ image tokens, as well as increases image diversities. NestAR further incorporates flow matching loss to use continuous tokens, and develops objectives to coordinate these multi-scale modules in model training. NestAR achieves competitive image generation performance while significantly lowering computational cost.

FAME: Fairness-aware Attention-modulated Video Editing

Training-free video editing (VE) models tend to fall back on gender stereotypes when rendering profession-related prompts. We propose \textbf{FAME} for \textit{Fairness-aware Attention-modulated Video Editing} that mitigates profession-related gender biases while preserving prompt alignment and temporal consistency for coherent VE. We derive fairness embeddings from existing minority representations by softly injecting debiasing tokens into the text encoder. Simultaneously, FAME integrates fairness modulation into both temporal self attention and prompt-to-region cross attention to mitigate the motion corruption and temporal inconsistency caused by directly introducing fairness cues. For temporal self attention, FAME introduces a region constrained attention mask combined with time decay weighting, which enhances intra-region coherence while suppressing irrelevant inter-region interactions. For cross attention, it reweights tokens to region matching scores by incorporating fairness sensitive similarity masks derived from debiasing prompt embeddings. Together, these modulations keep fairness-sensitive semantics tied to the right visual regions and prevent temporal drift across frames. Extensive experiments on new VE fairness-oriented benchmark \textit{FairVE} demonstrate that FAME achieves stronger fairness alignment and semantic fidelity, surpassing existing VE baselines.

VALA: Learning Latent Anchors for Training-Free and Temporally Consistent

Recent advances in training-free video editing have enabled lightweight and precise cross-frame generation by leveraging pre-trained text-to-image diffusion models. However, existing methods often rely on heuristic frame selection to maintain temporal consistency during DDIM inversion, which introduces manual bias and reduces the scalability of end-to-end inference. In this paper, we propose~\textbf{VALA} (\textbf{V}ariational \textbf{A}lignment for \textbf{L}atent \textbf{A}nchors), a variational alignment module that adaptively selects key frames and compresses their latent features into semantic anchors for consistent video editing. To learn meaningful assignments, VALA propose a variational framework with a contrastive learning objective. Therefore, it can transform cross-frame latent representations into compressed latent anchors that preserve both content and temporal coherence. Our method can be fully integrated into training-free text-to-image based video editing models. Extensive experiments on real-world video editing benchmarks show that VALA achieves state-of-the-art performance in inversion fidelity, editing quality, and temporal consistency, while offering improved efficiency over prior methods.

FigBO: A Generalized Acquisition Function Framework with Look-Ahead Capability for Bayesian Optimization

Bayesian optimization is a powerful technique for optimizing expensive-to-evaluate black-box functions, consisting of two main components: a surrogate model and an acquisition function. In recent years, myopic acquisition functions have been widely adopted for their simplicity and effectiveness. However, their lack of look-ahead capability limits their performance. To address this limitation, we propose FigBO, a generalized acquisition function that incorporates the future impact of candidate points on global information gain. FigBO is a plug-and-play method that can integrate seamlessly with most existing myopic acquisition functions. Theoretically, we analyze the regret bound and convergence rate of FigBO when combined with the myopic base acquisition function expected improvement (EI), comparing them to those of standard EI. Empirically, extensive experimental results across diverse tasks demonstrate that FigBO achieves state-of-the-art performance and significantly faster convergence compared to existing methods.

TraFlow: Trajectory Distillation on Pre-Trained Rectified Flow

Majorities of distillation methods on pre-trained diffusion models or on pre-trained rectified flow, focus on either the distillation outputs or the trajectories between random noises and clean images to speed up sample generations from pre-trained models. In those trajectory-based distillation methods, consistency distillation requires the self-consistent trajectory projection to regulate the trajectory, which might avoid the common ODE approximation error {while still be concerning about sampling efficiencies}. At the same time, rectified flow distillations enforce straight trajectory for fast sampling, although an ODE solver is still required. In this work, we propose a trajectory distillation method, \modelname, that enjoys the benefits of both and enables few-step generations. TraFlow adopts the settings of consistency trajectory models, and further enforces the properties of self-consistency and straightness throughout the entire trajectory. These two properties are pursued by reaching a balance with following three targets: (1) reconstruct the output from pre-trained models; (2) learn the amount of changes by pre-trained models; (3) satisfy the self-consistency over its trajectory. Extensive experimental results have shown the effectiveness of our proposed method.

A Survey on Pre-Trained Diffusion Model Distillations

Diffusion Models~(DMs) have emerged as the dominant approach in Generative Artificial Intelligence (GenAI), owing to their remarkable performance in tasks such as text-to-image synthesis. However, practical DMs, such as stable diffusion, are typically trained on massive datasets and thus usually require large storage. At the same time, many steps may be required, i.e., recursively evaluating the trained neural network, to generate a high-quality image, which results in significant computational costs during sample generation. As a result, distillation methods on pre-trained DM have become widely adopted practices to develop smaller, more efficient models capable of rapid, few-step generation in low-resource environment. When these distillation methods are developed from different perspectives, there is an urgent need for a systematic survey, particularly from a methodological perspective. In this survey, we review distillation methods through three aspects: output loss distillation, trajectory distillation and adversarial distillation. We also discuss current challenges and outline future research directions in the conclusion.

Navigating Towards Fairness with Data Selection

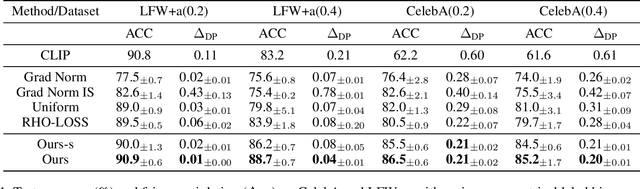
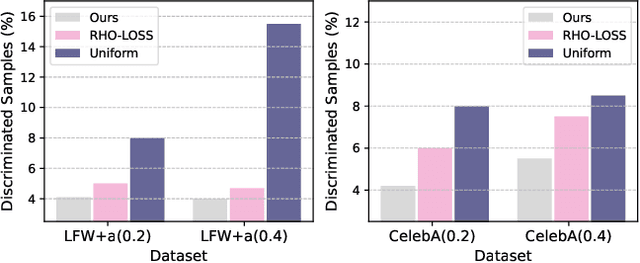
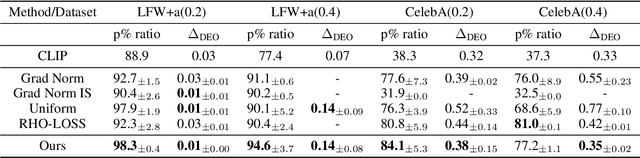
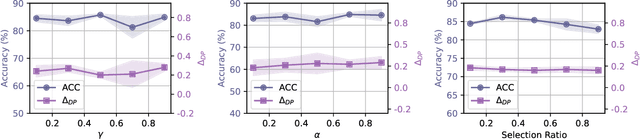
Machine learning algorithms often struggle to eliminate inherent data biases, particularly those arising from unreliable labels, which poses a significant challenge in ensuring fairness. Existing fairness techniques that address label bias typically involve modifying models and intervening in the training process, but these lack flexibility for large-scale datasets. To address this limitation, we introduce a data selection method designed to efficiently and flexibly mitigate label bias, tailored to more practical needs. Our approach utilizes a zero-shot predictor as a proxy model that simulates training on a clean holdout set. This strategy, supported by peer predictions, ensures the fairness of the proxy model and eliminates the need for an additional holdout set, which is a common requirement in previous methods. Without altering the classifier's architecture, our modality-agnostic method effectively selects appropriate training data and has proven efficient and effective in handling label bias and improving fairness across diverse datasets in experimental evaluations.

Marked Temporal Bayesian Flow Point Processes

Marked event data captures events by recording their continuous-valued occurrence timestamps along with their corresponding discrete-valued types. They have appeared in various real-world scenarios such as social media, financial transactions, and healthcare records, and have been effectively modeled through Marked Temporal Point Process (MTPP) models. Recently, developing generative models for these MTPP models have seen rapid development due to their powerful generative capability and less restrictive functional forms. However, existing generative MTPP models are usually challenged in jointly modeling events' timestamps and types since: (1) mainstream methods design the generative mechanisms for timestamps only and do not include event types; (2) the complex interdependence between the timestamps and event types are overlooked. In this paper, we propose a novel generative MTPP model called BMTPP. Unlike existing generative MTPP models, BMTPP flexibly models marked temporal joint distributions using a parameter-based approach. Additionally, by adding joint noise to the marked temporal data space, BMTPP effectively captures and explicitly reveals the interdependence between timestamps and event types. Extensive experiments validate the superiority of our approach over other state-of-the-art models and its ability to effectively capture marked-temporal interdependence.

Learning Coupled Subspaces for Multi-Condition Spike Data

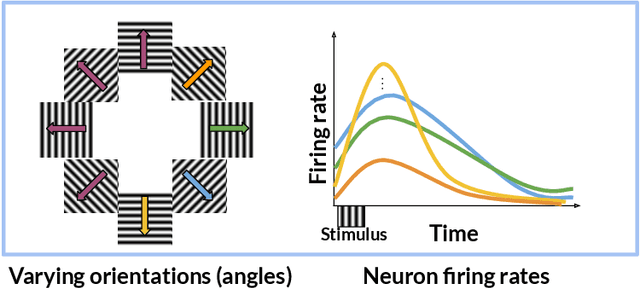
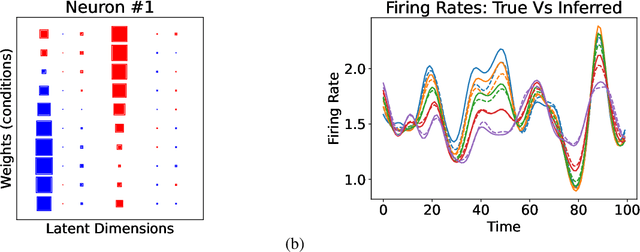
In neuroscience, researchers typically conduct experiments under multiple conditions to acquire neural responses in the form of high-dimensional spike train datasets. Analysing high-dimensional spike data is a challenging statistical problem. To this end, Gaussian process factor analysis (GPFA), a popular class of latent variable models has been proposed. GPFA extracts smooth, low-dimensional latent trajectories underlying high-dimensional spike train datasets. However, such analyses are often done separately for each experimental condition, contrary to the nature of neural datasets, which contain recordings under multiple experimental conditions. Exploiting the parametric nature of these conditions, we propose a multi-condition GPFA model and inference procedure to learn the underlying latent structure in the corresponding datasets in sample-efficient manner. In particular, we propose a non-parametric Bayesian approach to learn a smooth tuning function over the experiment condition space. Our approach not only boosts model accuracy and is faster, but also improves model interpretability compared to approaches that separately fit models for each experimental condition.

Federated Neural Nonparametric Point Processes

Temporal point processes (TPPs) are effective for modeling event occurrences over time, but they struggle with sparse and uncertain events in federated systems, where privacy is a major concern. To address this, we propose \textit{FedPP}, a Federated neural nonparametric Point Process model. FedPP integrates neural embeddings into Sigmoidal Gaussian Cox Processes (SGCPs) on the client side, which is a flexible and expressive class of TPPs, allowing it to generate highly flexible intensity functions that capture client-specific event dynamics and uncertainties while efficiently summarizing historical records. For global aggregation, FedPP introduces a divergence-based mechanism that communicates the distributions of SGCPs' kernel hyperparameters between the server and clients, while keeping client-specific parameters local to ensure privacy and personalization. FedPP effectively captures event uncertainty and sparsity, and extensive experiments demonstrate its superior performance in federated settings, particularly with KL divergence and Wasserstein distance-based global aggregation.