Learning Coupled Subspaces for Multi-Condition Spike Data
Paper and Code
Oct 24, 2024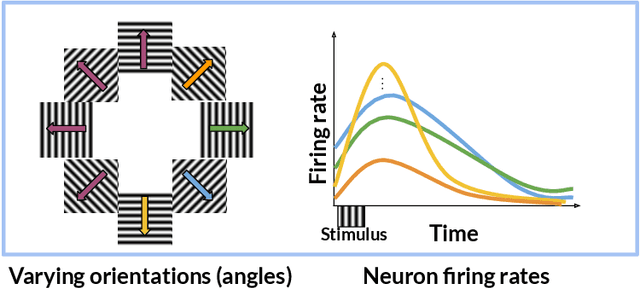

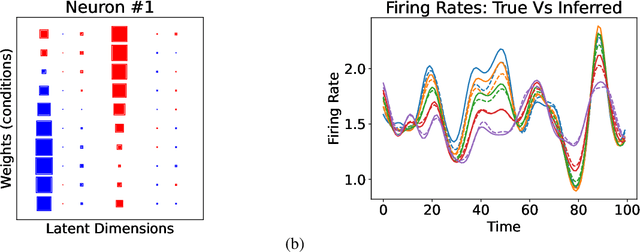

In neuroscience, researchers typically conduct experiments under multiple conditions to acquire neural responses in the form of high-dimensional spike train datasets. Analysing high-dimensional spike data is a challenging statistical problem. To this end, Gaussian process factor analysis (GPFA), a popular class of latent variable models has been proposed. GPFA extracts smooth, low-dimensional latent trajectories underlying high-dimensional spike train datasets. However, such analyses are often done separately for each experimental condition, contrary to the nature of neural datasets, which contain recordings under multiple experimental conditions. Exploiting the parametric nature of these conditions, we propose a multi-condition GPFA model and inference procedure to learn the underlying latent structure in the corresponding datasets in sample-efficient manner. In particular, we propose a non-parametric Bayesian approach to learn a smooth tuning function over the experiment condition space. Our approach not only boosts model accuracy and is faster, but also improves model interpretability compared to approaches that separately fit models for each experimental condition.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge