Learning Coupled Subspaces for Multi-Condition Spike Data

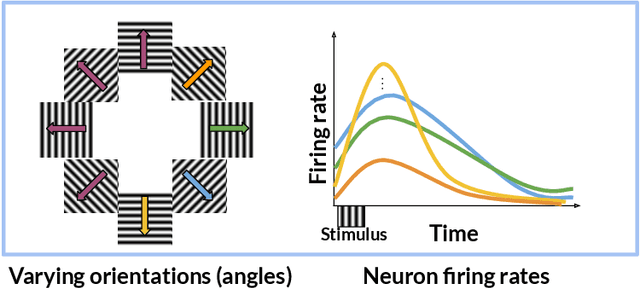
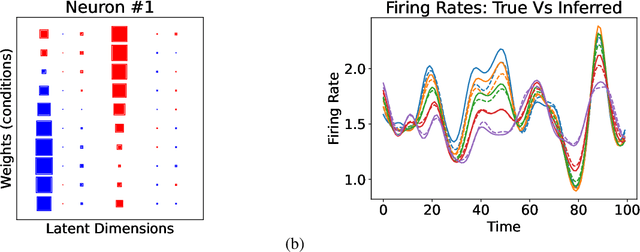
In neuroscience, researchers typically conduct experiments under multiple conditions to acquire neural responses in the form of high-dimensional spike train datasets. Analysing high-dimensional spike data is a challenging statistical problem. To this end, Gaussian process factor analysis (GPFA), a popular class of latent variable models has been proposed. GPFA extracts smooth, low-dimensional latent trajectories underlying high-dimensional spike train datasets. However, such analyses are often done separately for each experimental condition, contrary to the nature of neural datasets, which contain recordings under multiple experimental conditions. Exploiting the parametric nature of these conditions, we propose a multi-condition GPFA model and inference procedure to learn the underlying latent structure in the corresponding datasets in sample-efficient manner. In particular, we propose a non-parametric Bayesian approach to learn a smooth tuning function over the experiment condition space. Our approach not only boosts model accuracy and is faster, but also improves model interpretability compared to approaches that separately fit models for each experimental condition.

Conditionally-Conjugate Gaussian Process Factor Analysis for Spike Count Data via Data Augmentation

Gaussian process factor analysis (GPFA) is a latent variable modeling technique commonly used to identify smooth, low-dimensional latent trajectories underlying high-dimensional neural recordings. Specifically, researchers model spiking rates as Gaussian observations, resulting in tractable inference. Recently, GPFA has been extended to model spike count data. However, due to the non-conjugacy of the likelihood, the inference becomes intractable. Prior works rely on either black-box inference techniques, numerical integration or polynomial approximations of the likelihood to handle intractability. To overcome this challenge, we propose a conditionally-conjugate Gaussian process factor analysis (ccGPFA) resulting in both analytically and computationally tractable inference for modeling neural activity from spike count data. In particular, we develop a novel data augmentation based method that renders the model conditionally conjugate. Consequently, our model enjoys the advantage of simple closed-form updates using a variational EM algorithm. Furthermore, due to its conditional conjugacy, we show our model can be readily scaled using sparse Gaussian Processes and accelerated inference via natural gradients. To validate our method, we empirically demonstrate its efficacy through experiments.

Unified Projection-Free Algorithms for Adversarial DR-Submodular Optimization

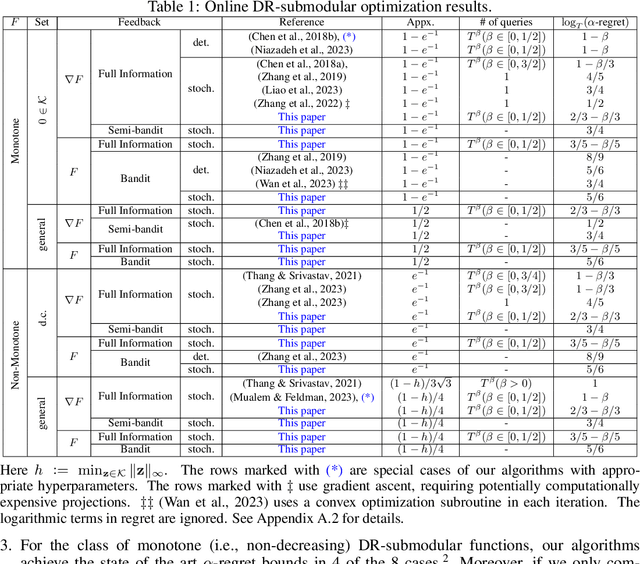
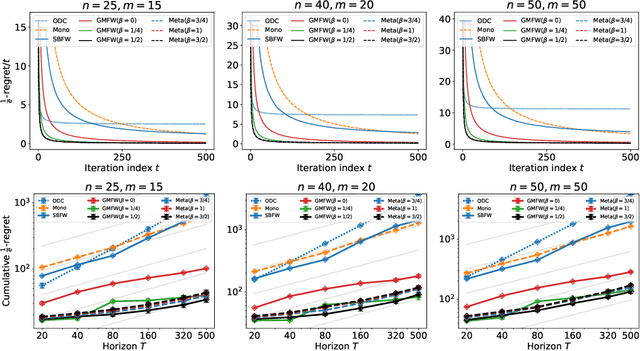
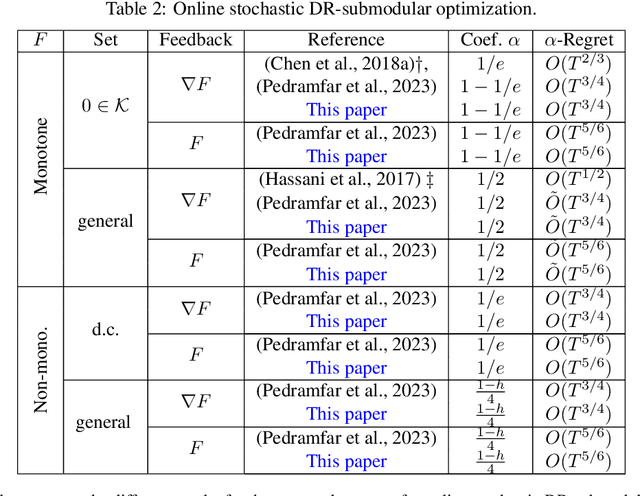
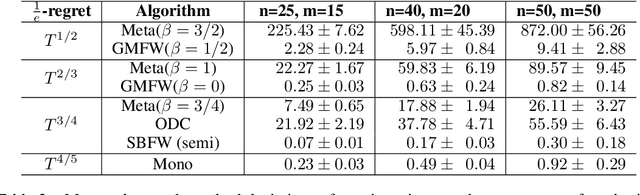
This paper introduces unified projection-free Frank-Wolfe type algorithms for adversarial continuous DR-submodular optimization, spanning scenarios such as full information and (semi-)bandit feedback, monotone and non-monotone functions, different constraints, and types of stochastic queries. For every problem considered in the non-monotone setting, the proposed algorithms are either the first with proven sub-linear $\alpha$-regret bounds or have better $\alpha$-regret bounds than the state of the art, where $\alpha$ is a corresponding approximation bound in the offline setting. In the monotone setting, the proposed approach gives state-of-the-art sub-linear $\alpha$-regret bounds among projection-free algorithms in 7 of the 8 considered cases while matching the result of the remaining case. Additionally, this paper addresses semi-bandit and bandit feedback for adversarial DR-submodular optimization, advancing the understanding of this optimization area.

DART: aDaptive Accept RejecT for non-linear top-K subset identification

We consider the bandit problem of selecting $K$ out of $N$ arms at each time step. The reward can be a non-linear function of the rewards of the selected individual arms. The direct use of a multi-armed bandit algorithm requires choosing among $\binom{N}{K}$ options, making the action space large. To simplify the problem, existing works on combinatorial bandits {typically} assume feedback as a linear function of individual rewards. In this paper, we prove the lower bound for top-$K$ subset selection with bandit feedback with possibly correlated rewards. We present a novel algorithm for the combinatorial setting without using individual arm feedback or requiring linearity of the reward function. Additionally, our algorithm works on correlated rewards of individual arms. Our algorithm, aDaptive Accept RejecT (DART), sequentially finds good arms and eliminates bad arms based on confidence bounds. DART is computationally efficient and uses storage linear in $N$. Further, DART achieves a regret bound of $\tilde{\mathcal{O}}(K\sqrt{KNT})$ for a time horizon $T$, which matches the lower bound in bandit feedback up to a factor of $\sqrt{\log{2NT}}$. When applied to the problem of cross-selling optimization and maximizing the mean of individual rewards, the performance of the proposed algorithm surpasses that of state-of-the-art algorithms. We also show that DART significantly outperforms existing methods for both linear and non-linear joint reward environments.

Directed Information Graphs

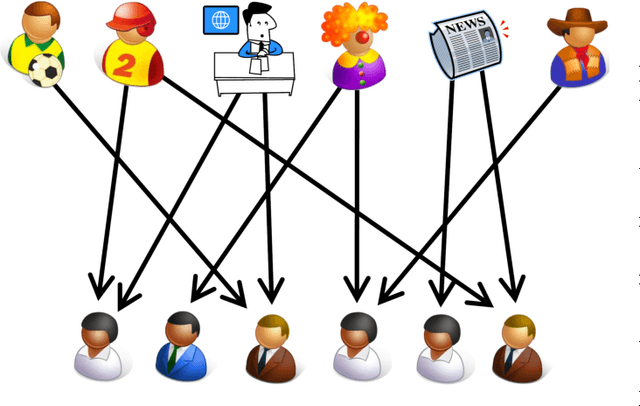
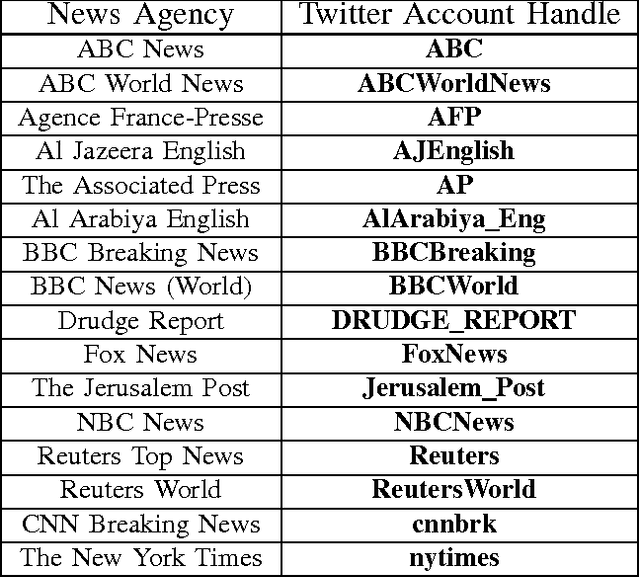
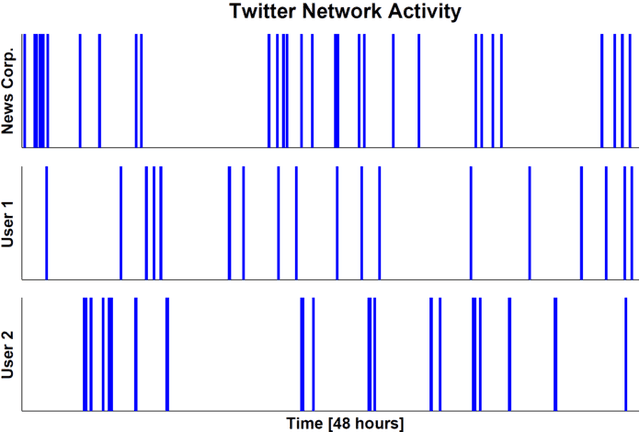
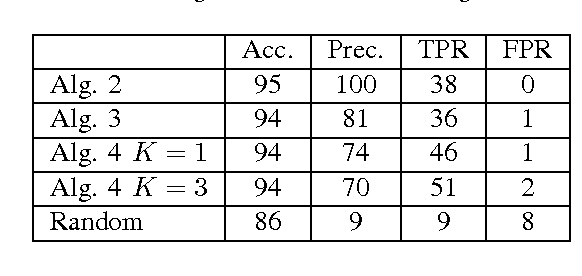
We propose a graphical model for representing networks of stochastic processes, the minimal generative model graph. It is based on reduced factorizations of the joint distribution over time. We show that under appropriate conditions, it is unique and consistent with another type of graphical model, the directed information graph, which is based on a generalization of Granger causality. We demonstrate how directed information quantifies Granger causality in a particular sequential prediction setting. We also develop efficient methods to estimate the topological structure from data that obviate estimating the joint statistics. One algorithm assumes upper-bounds on the degrees and uses the minimal dimension statistics necessary. In the event that the upper-bounds are not valid, the resulting graph is nonetheless an optimal approximation. Another algorithm uses near-minimal dimension statistics when no bounds are known but the distribution satisfies a certain criterion. Analogous to how structure learning algorithms for undirected graphical models use mutual information estimates, these algorithms use directed information estimates. We characterize the sample-complexity of two plug-in directed information estimators and obtain confidence intervals. For the setting when point estimates are unreliable, we propose an algorithm that uses confidence intervals to identify the best approximation that is robust to estimation error. Lastly, we demonstrate the effectiveness of the proposed algorithms through analysis of both synthetic data and real data from the Twitter network. In the latter case, we identify which news sources influence users in the network by merely analyzing tweet times.