Learning Coupled Subspaces for Multi-Condition Spike Data

In neuroscience, researchers typically conduct experiments under multiple conditions to acquire neural responses in the form of high-dimensional spike train datasets. Analysing high-dimensional spike data is a challenging statistical problem. To this end, Gaussian process factor analysis (GPFA), a popular class of latent variable models has been proposed. GPFA extracts smooth, low-dimensional latent trajectories underlying high-dimensional spike train datasets. However, such analyses are often done separately for each experimental condition, contrary to the nature of neural datasets, which contain recordings under multiple experimental conditions. Exploiting the parametric nature of these conditions, we propose a multi-condition GPFA model and inference procedure to learn the underlying latent structure in the corresponding datasets in sample-efficient manner. In particular, we propose a non-parametric Bayesian approach to learn a smooth tuning function over the experiment condition space. Our approach not only boosts model accuracy and is faster, but also improves model interpretability compared to approaches that separately fit models for each experimental condition.

Conditionally-Conjugate Gaussian Process Factor Analysis for Spike Count Data via Data Augmentation

Gaussian process factor analysis (GPFA) is a latent variable modeling technique commonly used to identify smooth, low-dimensional latent trajectories underlying high-dimensional neural recordings. Specifically, researchers model spiking rates as Gaussian observations, resulting in tractable inference. Recently, GPFA has been extended to model spike count data. However, due to the non-conjugacy of the likelihood, the inference becomes intractable. Prior works rely on either black-box inference techniques, numerical integration or polynomial approximations of the likelihood to handle intractability. To overcome this challenge, we propose a conditionally-conjugate Gaussian process factor analysis (ccGPFA) resulting in both analytically and computationally tractable inference for modeling neural activity from spike count data. In particular, we develop a novel data augmentation based method that renders the model conditionally conjugate. Consequently, our model enjoys the advantage of simple closed-form updates using a variational EM algorithm. Furthermore, due to its conditional conjugacy, we show our model can be readily scaled using sparse Gaussian Processes and accelerated inference via natural gradients. To validate our method, we empirically demonstrate its efficacy through experiments.

Unified Projection-Free Algorithms for Adversarial DR-Submodular Optimization

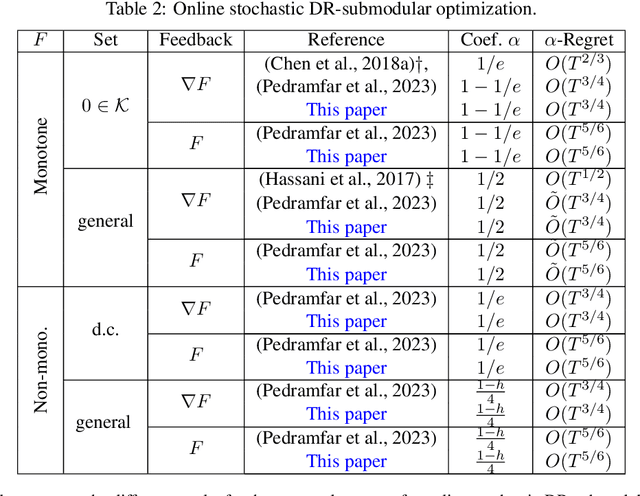
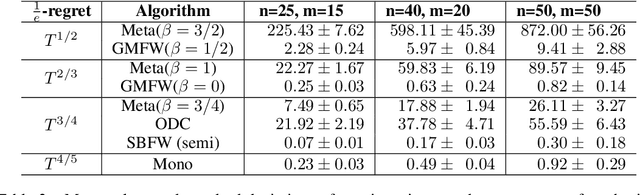
This paper introduces unified projection-free Frank-Wolfe type algorithms for adversarial continuous DR-submodular optimization, spanning scenarios such as full information and (semi-)bandit feedback, monotone and non-monotone functions, different constraints, and types of stochastic queries. For every problem considered in the non-monotone setting, the proposed algorithms are either the first with proven sub-linear $\alpha$-regret bounds or have better $\alpha$-regret bounds than the state of the art, where $\alpha$ is a corresponding approximation bound in the offline setting. In the monotone setting, the proposed approach gives state-of-the-art sub-linear $\alpha$-regret bounds among projection-free algorithms in 7 of the 8 considered cases while matching the result of the remaining case. Additionally, this paper addresses semi-bandit and bandit feedback for adversarial DR-submodular optimization, advancing the understanding of this optimization area.