Upper-Linearizability of Online Non-Monotone DR-Submodular Maximization over Down-Closed Convex Sets

We study online maximization of non-monotone Diminishing-Return(DR)-submodular functions over down-closed convex sets, a regime where existing projection-free online methods suffer from suboptimal regret and limited feedback guarantees. Our main contribution is a new structural result showing that this class is $1/e$-linearizable under carefully designed exponential reparametrization, scaling parameter, and surrogate potential, enabling a reduction to online linear optimization. As a result, we obtain $O(T^{1/2})$ static regret with a single gradient query per round and unlock adaptive and dynamic regret guarantees, together with improved rates under semi-bandit, bandit, and zeroth-order feedback. Across all feedback models, our bounds strictly improve the state of the art.

$γ$-weakly $θ$-up-concavity: Linearizable Non-Convex Optimization with Applications to DR-Submodular and OSS Functions

Optimizing monotone non-convex functions is a fundamental challenge across machine learning and combinatorial optimization. We introduce and study $γ$-weakly $θ$-up-concavity, a novel first-order condition that characterizes a broad class of such functions. This condition provides a powerful unifying framework, strictly generalizing both DR-submodular functions and One-Sided Smooth (OSS) functions. Our central theoretical contribution demonstrates that $γ$-weakly $θ$-up-concave functions are upper-linearizable: for any feasible point, we can construct a linear surrogate whose gains provably approximate the original non-linear objective. This approximation holds up to a constant factor, namely the approximation coefficient, dependent solely on $γ$, $θ$, and the geometry of the feasible set. This linearizability yields immediate and unified approximation guarantees for a wide range of problems. Specifically, we obtain unified approximation guarantees for offline optimization as well as static and dynamic regret bounds in online settings via standard reductions to linear optimization. Moreover, our framework recovers the optimal approximation coefficient for DR-submodular maximization and significantly improves existing approximation coefficients for OSS optimization, particularly over matroid constraints.

Diffusion Tree Sampling: Scalable inference-time alignment of diffusion models

Adapting a pretrained diffusion model to new objectives at inference time remains an open problem in generative modeling. Existing steering methods suffer from inaccurate value estimation, especially at high noise levels, which biases guidance. Moreover, information from past runs is not reused to improve sample quality, resulting in inefficient use of compute. Inspired by the success of Monte Carlo Tree Search, we address these limitations by casting inference-time alignment as a search problem that reuses past computations. We introduce a tree-based approach that samples from the reward-aligned target density by propagating terminal rewards back through the diffusion chain and iteratively refining value estimates with each additional generation. Our proposed method, Diffusion Tree Sampling (DTS), produces asymptotically exact samples from the target distribution in the limit of infinite rollouts, and its greedy variant, Diffusion Tree Search (DTS$^\star$), performs a global search for high reward samples. On MNIST and CIFAR-10 class-conditional generation, DTS matches the FID of the best-performing baseline with up to $10\times$ less compute. In text-to-image generation and language completion tasks, DTS$^\star$ effectively searches for high reward samples that match best-of-N with up to $5\times$ less compute. By reusing information from previous generations, we get an anytime algorithm that turns additional compute into steadily better samples, providing a scalable approach for inference-time alignment of diffusion models.

Order-Optimal Projection-Free Algorithm for Adversarially Constrained Online Convex Optimization

Projection-based algorithms for constrained Online Convex Optimization (COCO) face scalability challenges in high-dimensional settings due to the computational complexity of projecting iterates onto constraint sets. This paper introduces a projection-free algorithm for COCO that achieves state-of-the-art performance guarantees while eliminating the need for projections. By integrating a separation oracle with adaptive Online Gradient Descent (OGD) and employing a Lyapunov-driven surrogate function, while dynamically adjusting step sizes using gradient norms, our method jointly optimizes the regret and cumulative constraint violation (CCV). We also use a blocked version of OGD that helps achieve tradeoffs betweeen the regret and CCV with the number of calls to the separation oracle. For convex cost functions, our algorithm attains an optimal regret of $\mathcal{O}(\sqrt{T})$ and a CCV of $\mathcal{O}(\sqrt{T} \log T)$, matching the best-known projection-based results, while only using $\tilde{\mathcal{O}}({T})$ calls to the separation oracle. The results also demonstrate a tradeoff where lower calls to the separation oracle increase the regret and the CCV. In the strongly convex setting, we further achieve a regret of $\mathcal{O}(\log T)$ and a CCV of $\mathcal{O}(\sqrt{T\log T} )$, while requiring ${\mathcal{O}}({T}^2)$ calls to the separation oracle. Further, tradeoff with the decreasing oracle calls is studied. These results close the gap between projection-free and projection-based approaches, demonstrating that projection-free methods can achieve performance comparable to projection-based counterparts.

Decentralized Projection-free Online Upper-Linearizable Optimization with Applications to DR-Submodular Optimization

We introduce a novel framework for decentralized projection-free optimization, extending projection-free methods to a broader class of upper-linearizable functions. Our approach leverages decentralized optimization techniques with the flexibility of upper-linearizable function frameworks, effectively generalizing traditional DR-submodular function optimization. We obtain the regret of $O(T^{1-\theta/2})$ with communication complexity of $O(T^{\theta})$ and number of linear optimization oracle calls of $O(T^{2\theta})$ for decentralized upper-linearizable function optimization, for any $0\le \theta \le 1$. This approach allows for the first results for monotone up-concave optimization with general convex constraints and non-monotone up-concave optimization with general convex constraints. Further, the above results for first order feedback are extended to zeroth order, semi-bandit, and bandit feedback.

From Linear to Linearizable Optimization: A Novel Framework with Applications to Stationary and Non-stationary DR-submodular Optimization

This paper introduces the notion of upper linearizable/quadratizable functions, a class that extends concavity and DR-submodularity in various settings, including monotone and non-monotone cases over different convex sets. A general meta-algorithm is devised to convert algorithms for linear/quadratic maximization into ones that optimize upper quadratizable functions, offering a unified approach to tackling concave and DR-submodular optimization problems. The paper extends these results to multiple feedback settings, facilitating conversions between semi-bandit/first-order feedback and bandit/zeroth-order feedback, as well as between first/zeroth-order feedback and semi-bandit/bandit feedback. Leveraging this framework, new projection-free algorithms are derived using Follow The Perturbed Leader (FTPL) and other algorithms as base algorithms for linear/convex optimization, improving upon state-of-the-art results in various cases. Dynamic and adaptive regret guarantees are obtained for DR-submodular maximization, marking the first algorithms to achieve such guarantees in these settings. Notably, the paper achieves these advancements with fewer assumptions compared to existing state-of-the-art results, underscoring its broad applicability and theoretical contributions to non-convex optimization.

Unified Projection-Free Algorithms for Adversarial DR-Submodular Optimization

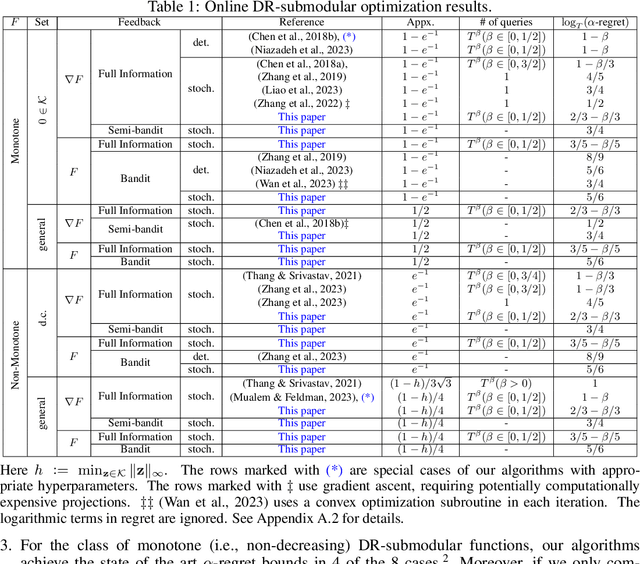
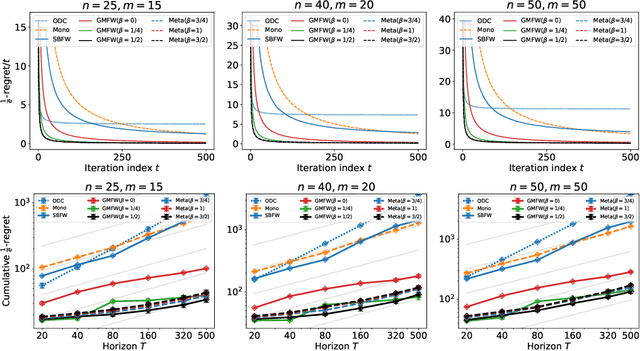
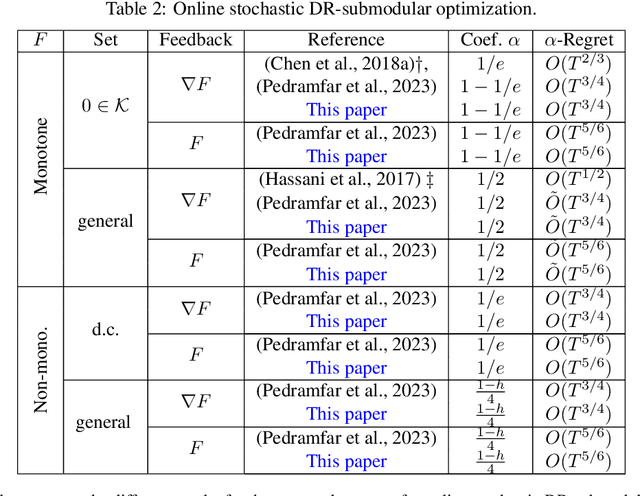
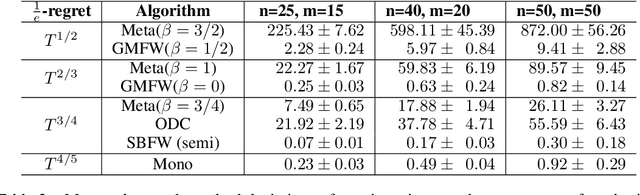
This paper introduces unified projection-free Frank-Wolfe type algorithms for adversarial continuous DR-submodular optimization, spanning scenarios such as full information and (semi-)bandit feedback, monotone and non-monotone functions, different constraints, and types of stochastic queries. For every problem considered in the non-monotone setting, the proposed algorithms are either the first with proven sub-linear $\alpha$-regret bounds or have better $\alpha$-regret bounds than the state of the art, where $\alpha$ is a corresponding approximation bound in the offline setting. In the monotone setting, the proposed approach gives state-of-the-art sub-linear $\alpha$-regret bounds among projection-free algorithms in 7 of the 8 considered cases while matching the result of the remaining case. Additionally, this paper addresses semi-bandit and bandit feedback for adversarial DR-submodular optimization, advancing the understanding of this optimization area.

A Generalized Approach to Online Convex Optimization

In this paper, we analyze the problem of online convex optimization in different settings. We show that any algorithm for online linear optimization with fully adaptive adversaries is an algorithm for online convex optimization. We also show that any such algorithm that requires full-information feedback may be transformed to an algorithm with semi-bandit feedback with comparable regret bound. We further show that algorithms that are designed for fully adaptive adversaries using deterministic semi-bandit feedback can obtain similar bounds using only stochastic semi-bandit feedback when facing oblivious adversaries. We use this to describe general meta-algorithms to convert first order algorithms to zeroth order algorithms with comparable regret bounds. Our framework allows us to analyze online optimization in various settings, such full-information feedback, bandit feedback, stochastic regret, adversarial regret and various forms of non-stationary regret. Using our analysis, we provide the first efficient projection-free online convex optimization algorithm using linear optimization oracles.

Improved Bayesian Regret Bounds for Thompson Sampling in Reinforcement Learning

In this paper, we prove the first Bayesian regret bounds for Thompson Sampling in reinforcement learning in a multitude of settings. We simplify the learning problem using a discrete set of surrogate environments, and present a refined analysis of the information ratio using posterior consistency. This leads to an upper bound of order $\widetilde{O}(H\sqrt{d_{l_1}T})$ in the time inhomogeneous reinforcement learning problem where $H$ is the episode length and $d_{l_1}$ is the Kolmogorov $l_1-$dimension of the space of environments. We then find concrete bounds of $d_{l_1}$ in a variety of settings, such as tabular, linear and finite mixtures, and discuss how how our results are either the first of their kind or improve the state-of-the-art.

A Unified Approach for Maximizing Continuous DR-submodular Functions

This paper presents a unified approach for maximizing continuous DR-submodular functions that encompasses a range of settings and oracle access types. Our approach includes a Frank-Wolfe type offline algorithm for both monotone and non-monotone functions, with different restrictions on the general convex set. We consider settings where the oracle provides access to either the gradient of the function or only the function value, and where the oracle access is either deterministic or stochastic. We determine the number of required oracle accesses in all cases. Our approach gives new/improved results for nine out of the sixteen considered cases, avoids computationally expensive projections in two cases, with the proposed framework matching performance of state-of-the-art approaches in the remaining five cases. Notably, our approach for the stochastic function value-based oracle enables the first regret bounds with bandit feedback for stochastic DR-submodular functions.