Improved Bayesian Regret Bounds for Thompson Sampling in Reinforcement Learning

In this paper, we prove the first Bayesian regret bounds for Thompson Sampling in reinforcement learning in a multitude of settings. We simplify the learning problem using a discrete set of surrogate environments, and present a refined analysis of the information ratio using posterior consistency. This leads to an upper bound of order $\widetilde{O}(H\sqrt{d_{l_1}T})$ in the time inhomogeneous reinforcement learning problem where $H$ is the episode length and $d_{l_1}$ is the Kolmogorov $l_1-$dimension of the space of environments. We then find concrete bounds of $d_{l_1}$ in a variety of settings, such as tabular, linear and finite mixtures, and discuss how how our results are either the first of their kind or improve the state-of-the-art.

Parameter Sharing in Coagent Networks

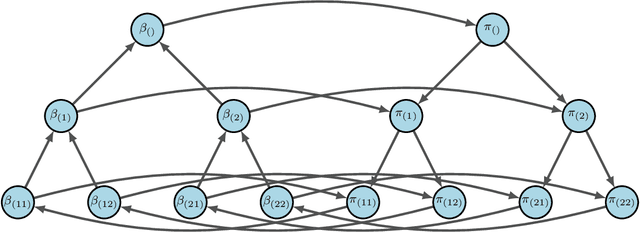
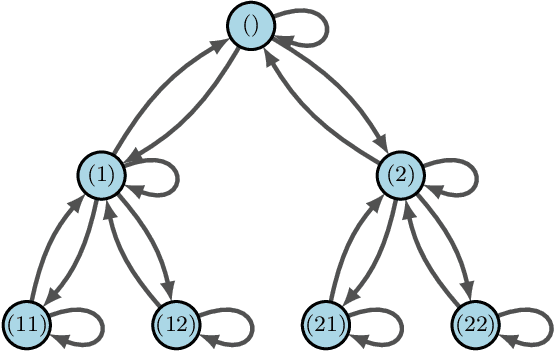
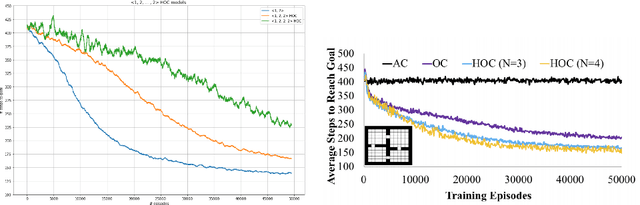
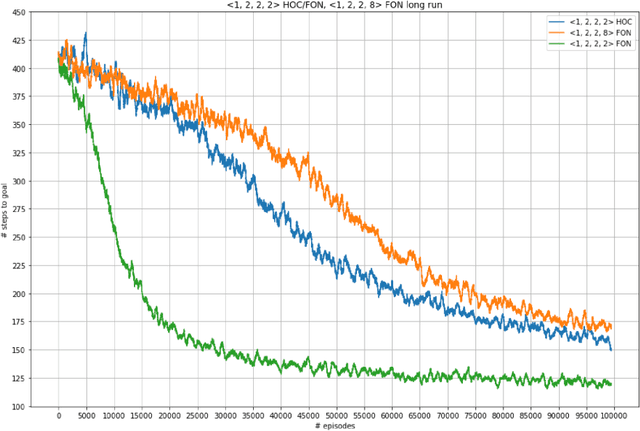
In this paper, we aim to prove the theorem that generalizes the Coagent Network Policy Gradient Theorem (Kostas et. al., 2019) to the context where parameters are shared among the function approximators involved. This provides the theoretical foundation to use any pattern of parameter sharing and leverage the freedom in the graph structure of the network to possibility exploit relational bias in a given task. As another application, we will apply our result to give a more intuitive proof for the Hierarchical Option Critic Policy Gradient Theorem, first shown in (Riemer et. al., 2019).