Bidirectional Normalizing Flow: From Data to Noise and Back

Normalizing Flows (NFs) have been established as a principled framework for generative modeling. Standard NFs consist of a forward process and a reverse process: the forward process maps data to noise, while the reverse process generates samples by inverting it. Typical NF forward transformations are constrained by explicit invertibility, ensuring that the reverse process can serve as their exact analytic inverse. Recent developments in TARFlow and its variants have revitalized NF methods by combining Transformers and autoregressive flows, but have also exposed causal decoding as a major bottleneck. In this work, we introduce Bidirectional Normalizing Flow ($\textbf{BiFlow}$), a framework that removes the need for an exact analytic inverse. BiFlow learns a reverse model that approximates the underlying noise-to-data inverse mapping, enabling more flexible loss functions and architectures. Experiments on ImageNet demonstrate that BiFlow, compared to its causal decoding counterpart, improves generation quality while accelerating sampling by up to two orders of magnitude. BiFlow yields state-of-the-art results among NF-based methods and competitive performance among single-evaluation ("1-NFE") methods. Following recent encouraging progress on NFs, we hope our work will draw further attention to this classical paradigm.

PrivacyXray: Detecting Privacy Breaches in LLMs through Semantic Consistency and Probability Certainty

Large Language Models (LLMs) are widely used in sensitive domains, including healthcare, finance, and legal services, raising concerns about potential private information leaks during inference. Privacy extraction attacks, such as jailbreaking, expose vulnerabilities in LLMs by crafting inputs that force the models to output sensitive information. However, these attacks cannot verify whether the extracted private information is accurate, as no public datasets exist for cross-validation, leaving a critical gap in private information detection during inference. To address this, we propose PrivacyXray, a novel framework detecting privacy breaches by analyzing LLM inner states. Our analysis reveals that LLMs exhibit higher semantic coherence and probabilistic certainty when generating correct private outputs. Based on this, PrivacyXray detects privacy breaches using four metrics: intra-layer and inter-layer semantic similarity, token-level and sentence-level probability distributions. PrivacyXray addresses critical challenges in private information detection by overcoming the lack of open-source private datasets and eliminating reliance on external data for validation. It achieves this through the synthesis of realistic private data and a detection mechanism based on the inner states of LLMs. Experiments show that PrivacyXray achieves consistent performance, with an average accuracy of 92.69% across five LLMs. Compared to state-of-the-art methods, PrivacyXray achieves significant improvements, with an average accuracy increase of 20.06%, highlighting its stability and practical utility in real-world applications.

H$^{\mathbf{3}}$DP: Triply-Hierarchical Diffusion Policy for Visuomotor Learning

Visuomotor policy learning has witnessed substantial progress in robotic manipulation, with recent approaches predominantly relying on generative models to model the action distribution. However, these methods often overlook the critical coupling between visual perception and action prediction. In this work, we introduce $\textbf{Triply-Hierarchical Diffusion Policy}~(\textbf{H$^{\mathbf{3}}$DP})$, a novel visuomotor learning framework that explicitly incorporates hierarchical structures to strengthen the integration between visual features and action generation. H$^{3}$DP contains $\mathbf{3}$ levels of hierarchy: (1) depth-aware input layering that organizes RGB-D observations based on depth information; (2) multi-scale visual representations that encode semantic features at varying levels of granularity; and (3) a hierarchically conditioned diffusion process that aligns the generation of coarse-to-fine actions with corresponding visual features. Extensive experiments demonstrate that H$^{3}$DP yields a $\mathbf{+27.5\%}$ average relative improvement over baselines across $\mathbf{44}$ simulation tasks and achieves superior performance in $\mathbf{4}$ challenging bimanual real-world manipulation tasks. Project Page: https://lyy-iiis.github.io/h3dp/.

Order-Optimal Projection-Free Algorithm for Adversarially Constrained Online Convex Optimization

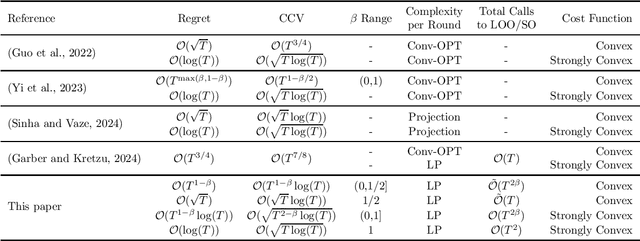
Projection-based algorithms for constrained Online Convex Optimization (COCO) face scalability challenges in high-dimensional settings due to the computational complexity of projecting iterates onto constraint sets. This paper introduces a projection-free algorithm for COCO that achieves state-of-the-art performance guarantees while eliminating the need for projections. By integrating a separation oracle with adaptive Online Gradient Descent (OGD) and employing a Lyapunov-driven surrogate function, while dynamically adjusting step sizes using gradient norms, our method jointly optimizes the regret and cumulative constraint violation (CCV). We also use a blocked version of OGD that helps achieve tradeoffs betweeen the regret and CCV with the number of calls to the separation oracle. For convex cost functions, our algorithm attains an optimal regret of $\mathcal{O}(\sqrt{T})$ and a CCV of $\mathcal{O}(\sqrt{T} \log T)$, matching the best-known projection-based results, while only using $\tilde{\mathcal{O}}({T})$ calls to the separation oracle. The results also demonstrate a tradeoff where lower calls to the separation oracle increase the regret and the CCV. In the strongly convex setting, we further achieve a regret of $\mathcal{O}(\log T)$ and a CCV of $\mathcal{O}(\sqrt{T\log T} )$, while requiring ${\mathcal{O}}({T}^2)$ calls to the separation oracle. Further, tradeoff with the decreasing oracle calls is studied. These results close the gap between projection-free and projection-based approaches, demonstrating that projection-free methods can achieve performance comparable to projection-based counterparts.

Decentralized Projection-free Online Upper-Linearizable Optimization with Applications to DR-Submodular Optimization

We introduce a novel framework for decentralized projection-free optimization, extending projection-free methods to a broader class of upper-linearizable functions. Our approach leverages decentralized optimization techniques with the flexibility of upper-linearizable function frameworks, effectively generalizing traditional DR-submodular function optimization. We obtain the regret of $O(T^{1-\theta/2})$ with communication complexity of $O(T^{\theta})$ and number of linear optimization oracle calls of $O(T^{2\theta})$ for decentralized upper-linearizable function optimization, for any $0\le \theta \le 1$. This approach allows for the first results for monotone up-concave optimization with general convex constraints and non-monotone up-concave optimization with general convex constraints. Further, the above results for first order feedback are extended to zeroth order, semi-bandit, and bandit feedback.

Dendritic Localized Learning: Toward Biologically Plausible Algorithm

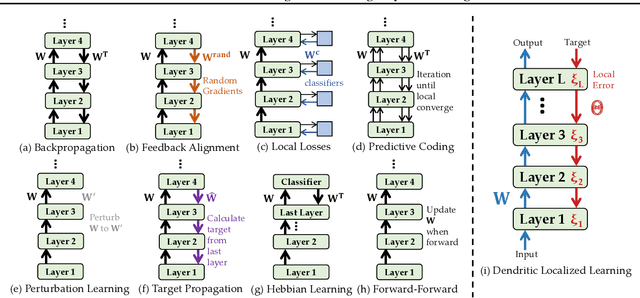
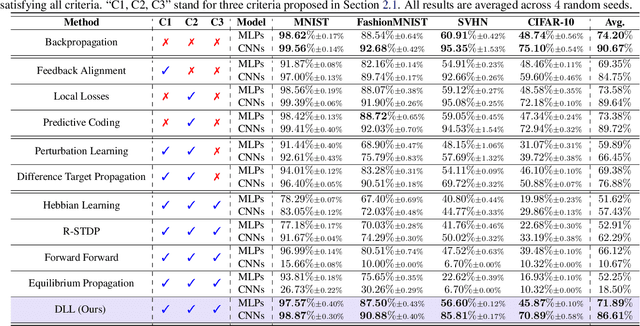
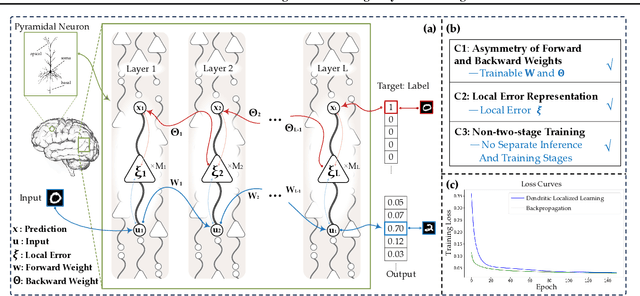
Backpropagation is the foundational algorithm for training neural networks and a key driver of deep learning's success. However, its biological plausibility has been challenged due to three primary limitations: weight symmetry, reliance on global error signals, and the dual-phase nature of training, as highlighted by the existing literature. Although various alternative learning approaches have been proposed to address these issues, most either fail to satisfy all three criteria simultaneously or yield suboptimal results. Inspired by the dynamics and plasticity of pyramidal neurons, we propose Dendritic Localized Learning (DLL), a novel learning algorithm designed to overcome these challenges. Extensive empirical experiments demonstrate that DLL satisfies all three criteria of biological plausibility while achieving state-of-the-art performance among algorithms that meet these requirements. Furthermore, DLL exhibits strong generalization across a range of architectures, including MLPs, CNNs, and RNNs. These results, benchmarked against existing biologically plausible learning algorithms, offer valuable empirical insights for future research. We hope this study can inspire the development of new biologically plausible algorithms for training multilayer networks and advancing progress in both neuroscience and machine learning.

FairEdit: Preserving Fairness in Graph Neural Networks through Greedy Graph Editing

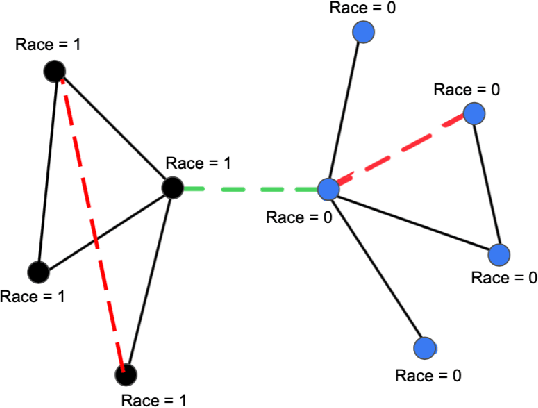
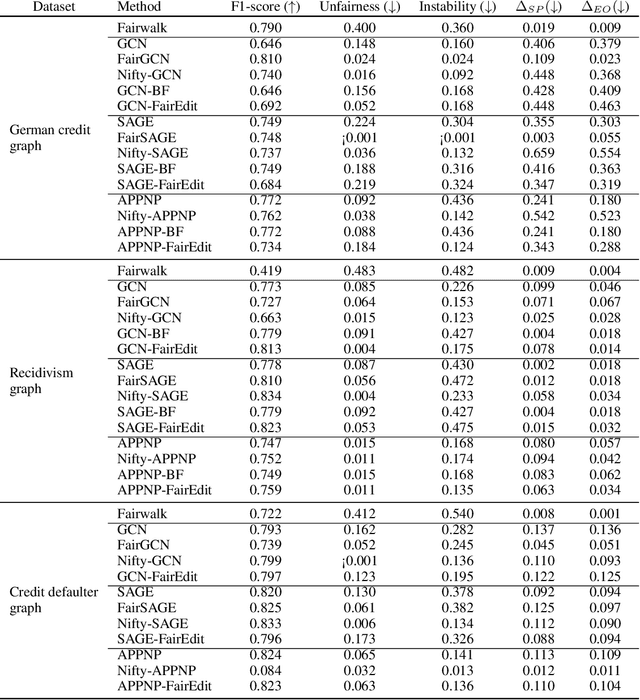
Graph Neural Networks (GNNs) have proven to excel in predictive modeling tasks where the underlying data is a graph. However, as GNNs are extensively used in human-centered applications, the issue of fairness has arisen. While edge deletion is a common method used to promote fairness in GNNs, it fails to consider when data is inherently missing fair connections. In this work we consider the unexplored method of edge addition, accompanied by deletion, to promote fairness. We propose two model-agnostic algorithms to perform edge editing: a brute force approach and a continuous approximation approach, FairEdit. FairEdit performs efficient edge editing by leveraging gradient information of a fairness loss to find edges that improve fairness. We find that FairEdit outperforms standard training for many data sets and GNN methods, while performing comparably to many state-of-the-art methods, demonstrating FairEdit's ability to improve fairness across many domains and models.