A Distributed Framework for the Construction of Transport Maps

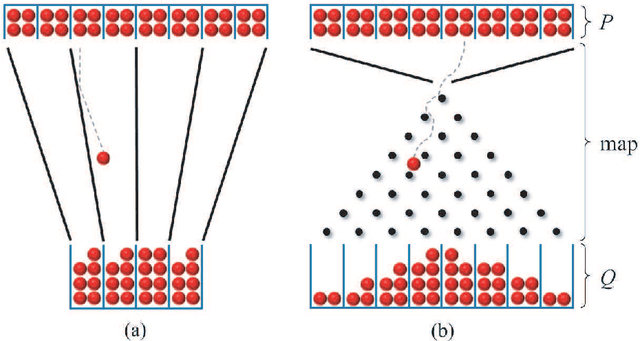
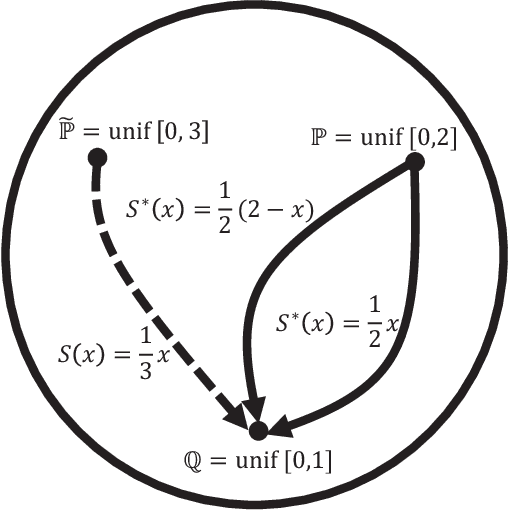
The need to reason about uncertainty in large, complex, and multi-modal datasets has become increasingly common across modern scientific environments. The ability to transform samples from one distribution $P$ to another distribution $Q$ enables the solution to many problems in machine learning (e.g. Bayesian inference, generative modeling) and has been actively pursued from theoretical, computational, and application perspectives across the fields of information theory, computer science, and biology. Performing such transformations, in general, still leads to computational difficulties, especially in high dimensions. Here, we consider the problem of computing such "measure transport maps" with efficient and parallelizable methods. Under the mild assumptions that $P$ need not be known but can be sampled from, and that the density of $Q$ is known up to a proportionality constant, and that $Q$ is log-concave, we provide in this work a convex optimization problem pertaining to relative entropy minimization. We show how an empirical minimization formulation and polynomial chaos map parameterization can allow for learning a transport map between $P$ and $Q$ with distributed and scalable methods. We also leverage findings from nonequilibrium thermodynamics to represent the transport map as a composition of simpler maps, each of which is learned sequentially with a transport cost regularized version of the aforementioned problem formulation. We provide examples of our framework within the context of Bayesian inference for the Boston housing dataset and generative modeling for handwritten digit images from the MNIST dataset.

Tractable Fully Bayesian Inference via Convex Optimization and Optimal Transport Theory

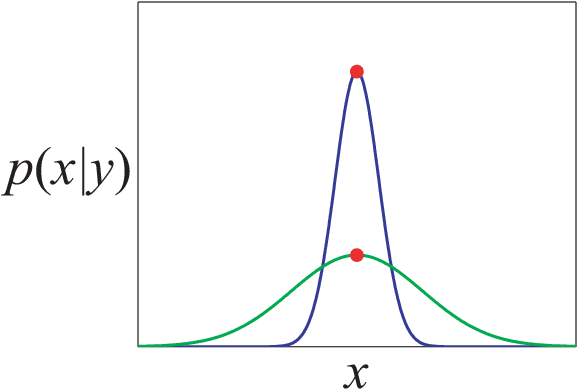
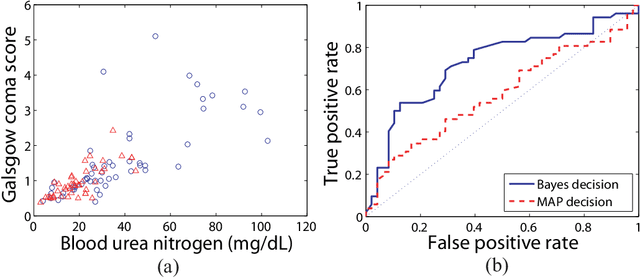
We consider the problem of transforming samples from one continuous source distribution into samples from another target distribution. We demonstrate with optimal transport theory that when the source distribution can be easily sampled from and the target distribution is log-concave, this can be tractably solved with convex optimization. We show that a special case of this, when the source is the prior and the target is the posterior, is Bayesian inference. Here, we can tractably calculate the normalization constant and draw posterior i.i.d. samples. Remarkably, our Bayesian tractability criterion is simply log concavity of the prior and likelihood: the same criterion for tractable calculation of the maximum a posteriori point estimate. With simulated data, we demonstrate how we can attain the Bayes risk in simulations. With physiologic data, we demonstrate improvements over point estimation in intensive care unit outcome prediction and electroencephalography-based sleep staging.

Directed Information Graphs

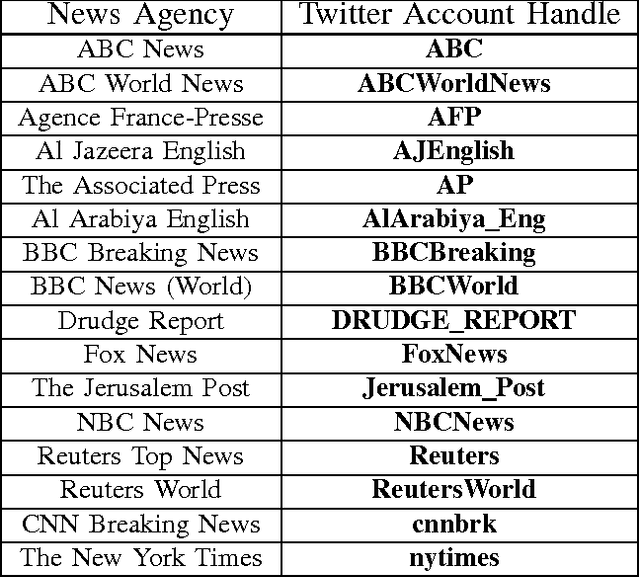
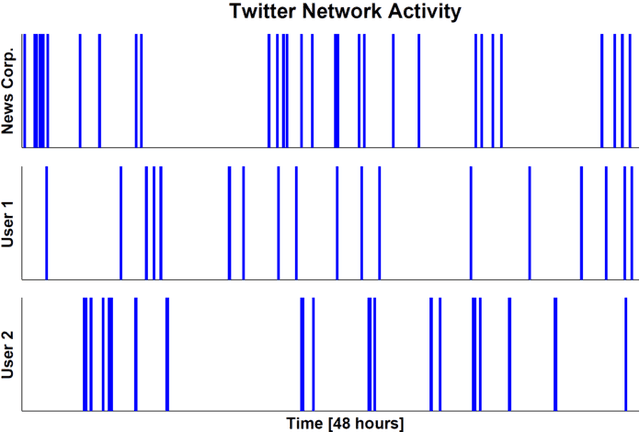
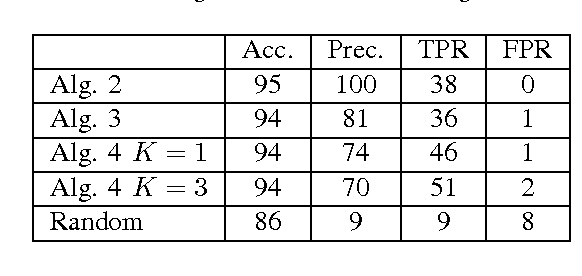
We propose a graphical model for representing networks of stochastic processes, the minimal generative model graph. It is based on reduced factorizations of the joint distribution over time. We show that under appropriate conditions, it is unique and consistent with another type of graphical model, the directed information graph, which is based on a generalization of Granger causality. We demonstrate how directed information quantifies Granger causality in a particular sequential prediction setting. We also develop efficient methods to estimate the topological structure from data that obviate estimating the joint statistics. One algorithm assumes upper-bounds on the degrees and uses the minimal dimension statistics necessary. In the event that the upper-bounds are not valid, the resulting graph is nonetheless an optimal approximation. Another algorithm uses near-minimal dimension statistics when no bounds are known but the distribution satisfies a certain criterion. Analogous to how structure learning algorithms for undirected graphical models use mutual information estimates, these algorithms use directed information estimates. We characterize the sample-complexity of two plug-in directed information estimators and obtain confidence intervals. For the setting when point estimates are unreliable, we propose an algorithm that uses confidence intervals to identify the best approximation that is robust to estimation error. Lastly, we demonstrate the effectiveness of the proposed algorithms through analysis of both synthetic data and real data from the Twitter network. In the latter case, we identify which news sources influence users in the network by merely analyzing tweet times.