Tractable Fully Bayesian Inference via Convex Optimization and Optimal Transport Theory
Paper and Code
Sep 29, 2015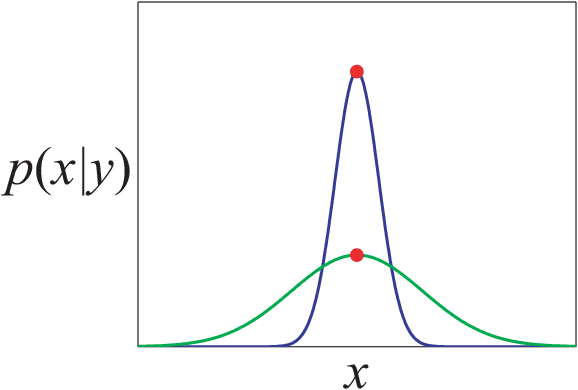
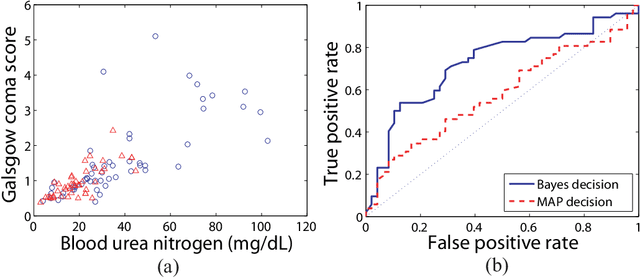
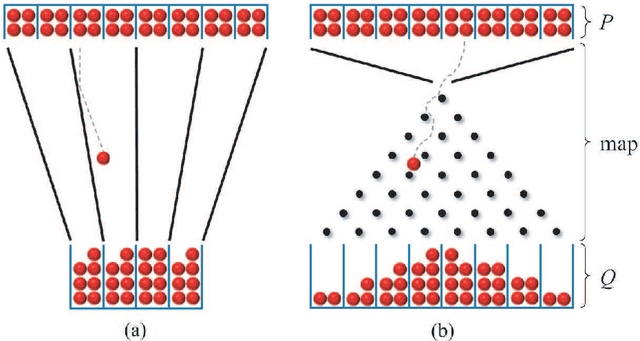
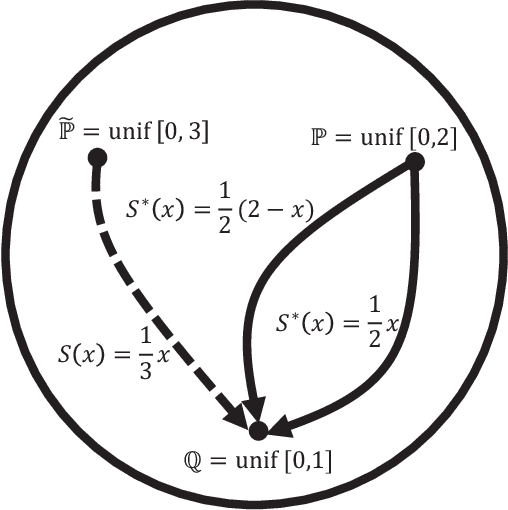
We consider the problem of transforming samples from one continuous source distribution into samples from another target distribution. We demonstrate with optimal transport theory that when the source distribution can be easily sampled from and the target distribution is log-concave, this can be tractably solved with convex optimization. We show that a special case of this, when the source is the prior and the target is the posterior, is Bayesian inference. Here, we can tractably calculate the normalization constant and draw posterior i.i.d. samples. Remarkably, our Bayesian tractability criterion is simply log concavity of the prior and likelihood: the same criterion for tractable calculation of the maximum a posteriori point estimate. With simulated data, we demonstrate how we can attain the Bayes risk in simulations. With physiologic data, we demonstrate improvements over point estimation in intensive care unit outcome prediction and electroencephalography-based sleep staging.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge