Rényi Neural Processes

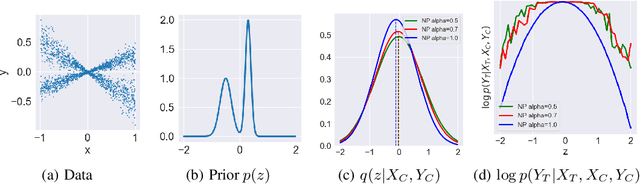
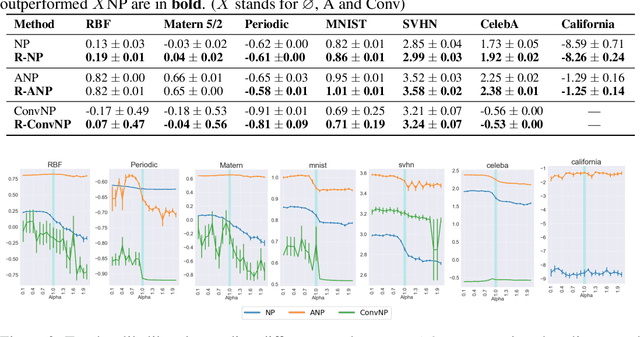
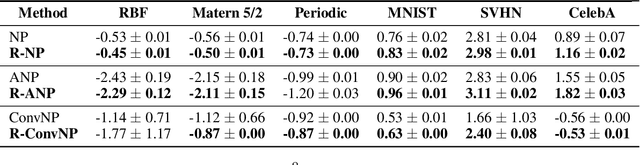
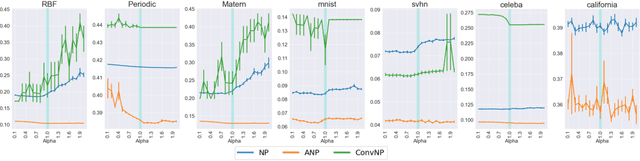
Neural Processes (NPs) are variational frameworks that aim to represent stochastic processes with deep neural networks. Despite their obvious benefits in uncertainty estimation for complex distributions via data-driven priors, NPs enforce network parameter sharing between the conditional prior and posterior distributions, thereby risking introducing a misspecified prior. We hereby propose R\'enyi Neural Processes (RNP) to relax the influence of the misspecified prior and optimize a tighter bound of the marginal likelihood. More specifically, by replacing the standard KL divergence with the R\'enyi divergence between the posterior and the approximated prior, we ameliorate the impact of the misspecified prior via a parameter {\alpha} so that the resulting posterior focuses more on tail samples and reduce density on overconfident regions. Our experiments showed log-likelihood improvements on several existing NP families. We demonstrated the superior performance of our approach on various benchmarks including regression and image inpainting tasks. We also validate the effectiveness of RNPs on real-world tabular regression problems.