Variational DAG Estimation via State Augmentation With Stochastic Permutations

Estimating the structure of a Bayesian network, in the form of a directed acyclic graph (DAG), from observational data is a statistically and computationally hard problem with essential applications in areas such as causal discovery. Bayesian approaches are a promising direction for solving this task, as they allow for uncertainty quantification and deal with well-known identifiability issues. From a probabilistic inference perspective, the main challenges are (i) representing distributions over graphs that satisfy the DAG constraint and (ii) estimating a posterior over the underlying combinatorial space. We propose an approach that addresses these challenges by formulating a joint distribution on an augmented space of DAGs and permutations. We carry out posterior estimation via variational inference, where we exploit continuous relaxations of discrete distributions. We show that our approach can outperform competitive Bayesian and non-Bayesian benchmarks on a range of synthetic and real datasets.

Addressing Over-Smoothing in Graph Neural Networks via Deep Supervision

Learning useful node and graph representations with graph neural networks (GNNs) is a challenging task. It is known that deep GNNs suffer from over-smoothing where, as the number of layers increases, node representations become nearly indistinguishable and model performance on the downstream task degrades significantly. To address this problem, we propose deeply-supervised GNNs (DSGNNs), i.e., GNNs enhanced with deep supervision where representations learned at all layers are used for training. We show empirically that DSGNNs are resilient to over-smoothing and can outperform competitive benchmarks on node and graph property prediction problems.

Variational Spectral Graph Convolutional Networks

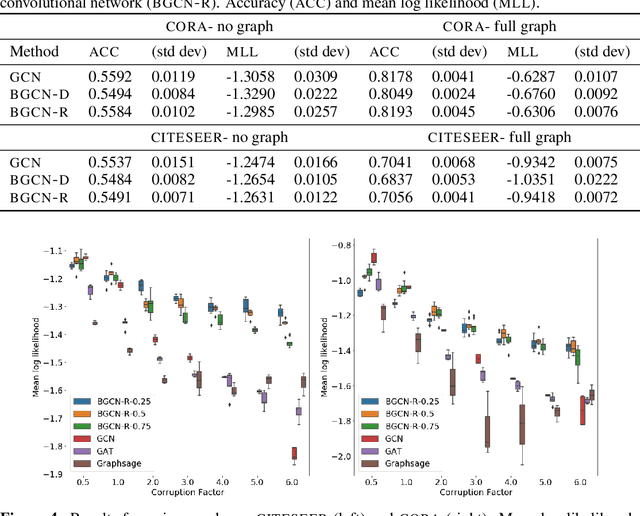
We propose a Bayesian approach to spectral graph convolutional networks (GCNs) where the graph parameters are considered as random variables. We develop an inference algorithm to estimate the posterior over these parameters and use it to incorporate prior information that is not naturally considered by standard GCN. The key to our approach is to define a smooth posterior parameterization over the adjacency matrix characterizing the graph, which we estimate via stochastic variational inference. Our experiments show that we can outperform standard GCN methods in the task of semi-supervised classification in noisy-graph regimes.