Agentic Bayesian Optimization through Surrogate-Augmented Autoresearch

Bayesian optimization (BO) has become the standard tool for sample-efficient optimization and owes its efficiency to uncertainty-aware search driven by generic statistical priors. Richer domain priors can improve BO in principle, but encoding them through tailored kernels or problem structure is difficult and rarely done in practice. LLMs can help sidestep this difficulty by making informal priors from natural language, code, and documentation directly available to the optimizer. However, existing LLM-based BO methods either insert the LLM into a fixed role (surrogate, acquisition proxy, or configuration interface) or hand it broad control, sacrificing the systematic exploration that makes BO reliable. We introduce agentic Bayesian optimization: a paradigm in which an LLM agent is the central decision maker in the BO loop while a Bayesian backend provides the uncertainty-aware optimization substrate. The agent configures the problem, queries the backend, selects and commits evaluations, and can revise the optimization strategy during the run by tightening bounds, switching acquisition functions, proposing targeted evaluations, or even reframing the problem following new instructions or observed evidence. We instantiate this idea in Sara, a surrogate-augmented autoresearch agent, and lenz, a modular BoTorch-based backend that the agent can inspect and modify through a structured interface. Across synthetic and real-world benchmarks, Sara preserves the reliability of state-of-the-art BO without prior knowledge, outperforms LLM-based baselines, and uses natural-language priors to improve beyond standard BO. We further demonstrate the practical value of agentic BO in dynamic settings, where Sara reconfigures the full optimization problem on the fly as requirements change, a capability not previously available in standard BO.

Batch Bayesian optimisation via density-ratio estimation with guarantees

Bayesian optimisation (BO) algorithms have shown remarkable success in applications involving expensive black-box functions. Traditionally BO has been set as a sequential decision-making process which estimates the utility of query points via an acquisition function and a prior over functions, such as a Gaussian process. Recently, however, a reformulation of BO via density-ratio estimation (BORE) allowed reinterpreting the acquisition function as a probabilistic binary classifier, removing the need for an explicit prior over functions and increasing scalability. In this paper, we present a theoretical analysis of BORE's regret and an extension of the algorithm with improved uncertainty estimates. We also show that BORE can be naturally extended to a batch optimisation setting by recasting the problem as approximate Bayesian inference. The resulting algorithm comes equipped with theoretical performance guarantees and is assessed against other batch BO baselines in a series of experiments.

Variational Spectral Graph Convolutional Networks

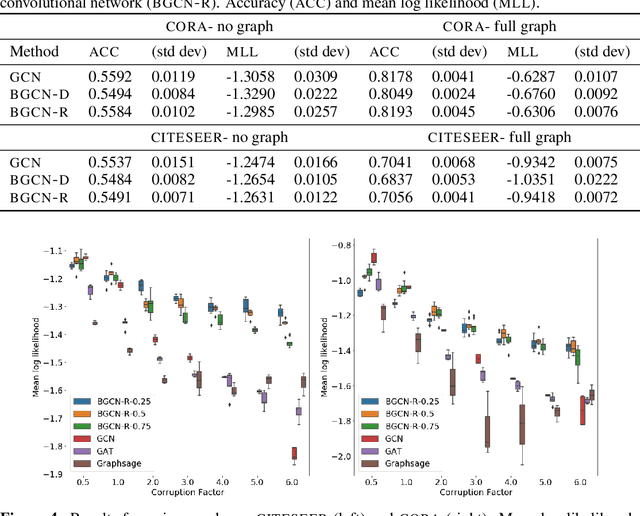
We propose a Bayesian approach to spectral graph convolutional networks (GCNs) where the graph parameters are considered as random variables. We develop an inference algorithm to estimate the posterior over these parameters and use it to incorporate prior information that is not naturally considered by standard GCN. The key to our approach is to define a smooth posterior parameterization over the adjacency matrix characterizing the graph, which we estimate via stochastic variational inference. Our experiments show that we can outperform standard GCN methods in the task of semi-supervised classification in noisy-graph regimes.