Amortized variational transdimensional inference

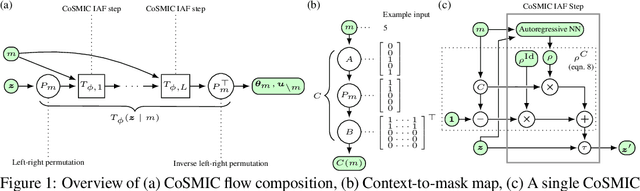
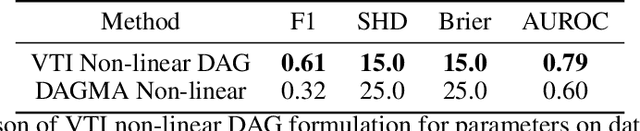
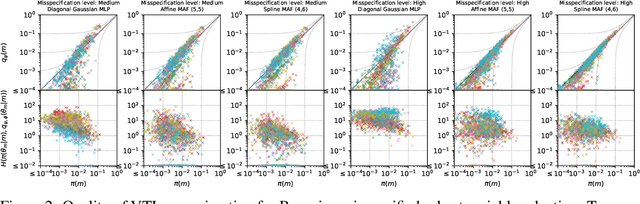
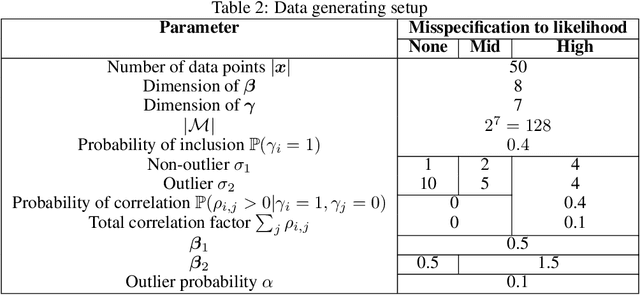
The expressiveness of flow-based models combined with stochastic variational inference (SVI) has, in recent years, expanded the application of optimization-based Bayesian inference to include problems with complex data relationships. However, until now, SVI using flow-based models has been limited to problems of fixed dimension. We introduce CoSMIC, normalizing flows (COntextually-Specified Masking for Identity-mapped Components), an extension to neural autoregressive conditional normalizing flow architectures that enables using a single amortized variational density for inference over a transdimensional target distribution. We propose a combined stochastic variational transdimensional inference (VTI) approach to training CoSMIC flows using techniques from Bayesian optimization and Monte Carlo gradient estimation. Numerical experiments demonstrate the performance of VTI on challenging problems that scale to high-cardinality model spaces.

Positional Encoder Graph Quantile Neural Networks for Geographic Data

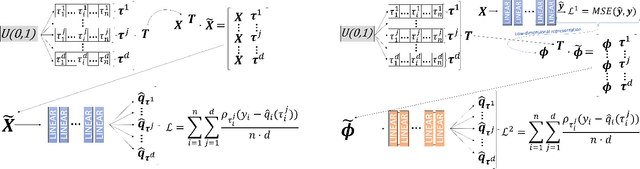
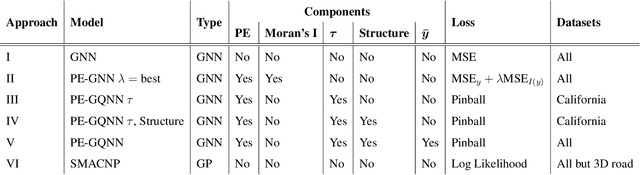
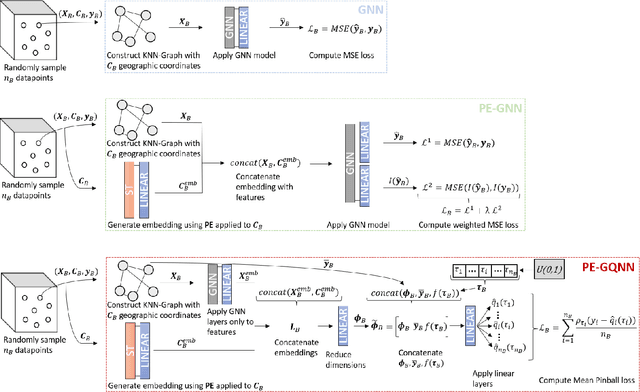
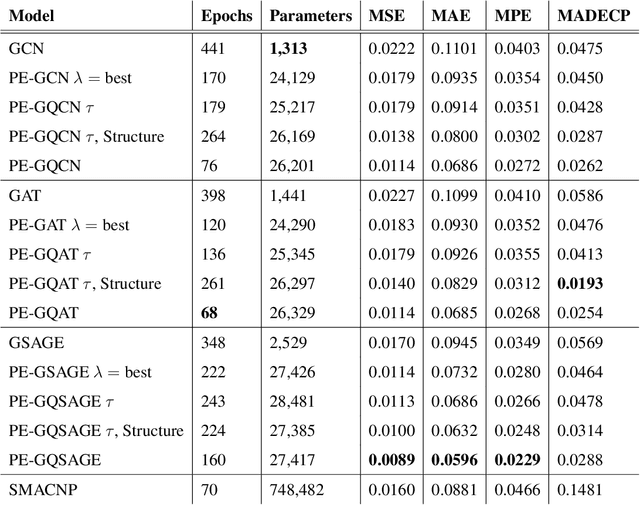
Positional Encoder Graph Neural Networks (PE-GNNs) are a leading approach for modeling continuous spatial data. However, they often fail to produce calibrated predictive distributions, limiting their effectiveness for uncertainty quantification. We introduce the Positional Encoder Graph Quantile Neural Network (PE-GQNN), a novel method that integrates PE-GNNs, Quantile Neural Networks, and recalibration techniques in a fully nonparametric framework, requiring minimal assumptions about the predictive distributions. We propose a new network architecture that, when combined with a quantile-based loss function, yields accurate and reliable probabilistic models without increasing computational complexity. Our approach provides a flexible, robust framework for conditional density estimation, applicable beyond spatial data contexts. We further introduce a structured method for incorporating a KNN predictor into the model while avoiding data leakage through the GNN layer operation. Experiments on benchmark datasets demonstrate that PE-GQNN significantly outperforms existing state-of-the-art methods in both predictive accuracy and uncertainty quantification.

Free-Form Variational Inference for Gaussian Process State-Space Models

Gaussian process state-space models (GPSSMs) provide a principled and flexible approach to modeling the dynamics of a latent state, which is observed at discrete-time points via a likelihood model. However, inference in GPSSMs is computationally and statistically challenging due to the large number of latent variables in the model and the strong temporal dependencies between them. In this paper, we propose a new method for inference in Bayesian GPSSMs, which overcomes the drawbacks of previous approaches, namely over-simplified assumptions, and high computational requirements. Our method is based on free-form variational inference via stochastic gradient Hamiltonian Monte Carlo within the inducing-variable formalism. Furthermore, by exploiting our proposed variational distribution, we provide a collapsed extension of our method where the inducing variables are marginalized analytically. We also showcase results when combining our framework with particle MCMC methods. We show that, on six real-world datasets, our approach can learn transition dynamics and latent states more accurately than competing methods.

Online Binary Space Partitioning Forests

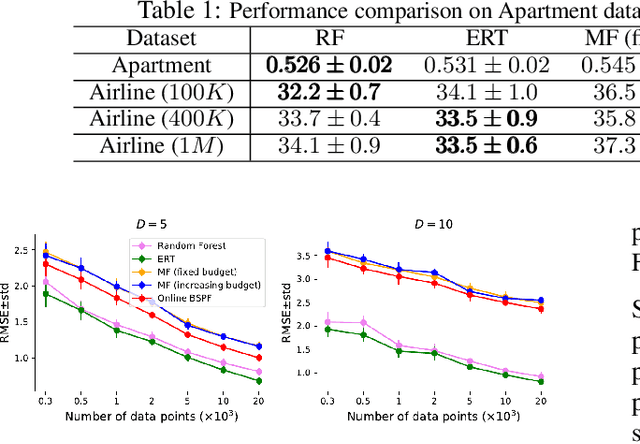
The Binary Space Partitioning-Tree~(BSP-Tree) process was recently proposed as an efficient strategy for space partitioning tasks. Because it uses more than one dimension to partition the space, the BSP-Tree Process is more efficient and flexible than conventional axis-aligned cutting strategies. However, due to its batch learning setting, it is not well suited to large-scale classification and regression problems. In this paper, we develop an online BSP-Forest framework to address this limitation. With the arrival of new data, the resulting online algorithm can simultaneously expand the space coverage and refine the partition structure, with guaranteed universal consistency for both classification and regression problems. The effectiveness and competitive performance of the online BSP-Forest is verified via simulations on real-world datasets.

Bayesian Nonparametric Space Partitions: A Survey

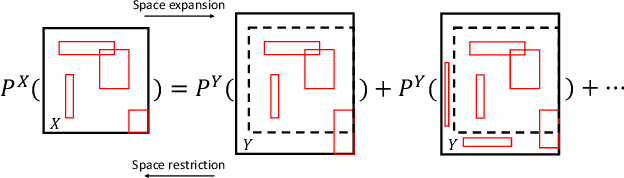
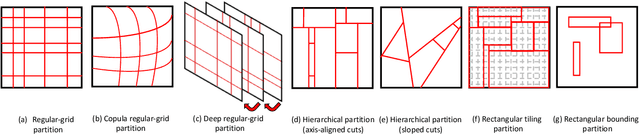
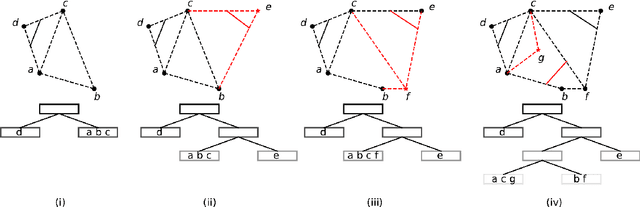
Bayesian nonparametric space partition (BNSP) models provide a variety of strategies for partitioning a $D$-dimensional space into a set of blocks. In this way, the data points lie in the same block would share certain kinds of homogeneity. BNSP models can be applied to various areas, such as regression/classification trees, random feature construction, relational modeling, etc. In this survey, we investigate the current progress of BNSP research through the following three perspectives: models, which review various strategies for generating the partitions in the space and discuss their theoretical foundation `self-consistency'; applications, which cover the current mainstream usages of BNSP models and their potential future practises; and challenges, which identify the current unsolved problems and valuable future research topics. As there are no comprehensive reviews of BNSP literature before, we hope that this survey can induce further exploration and exploitation on this topic.

Smoothing Graphons for Modelling Exchangeable Relational Data

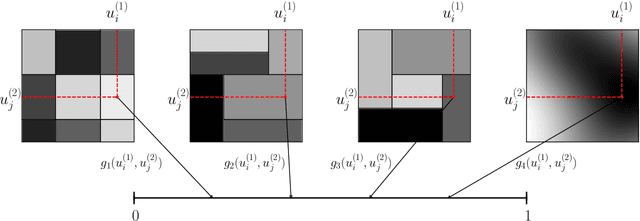
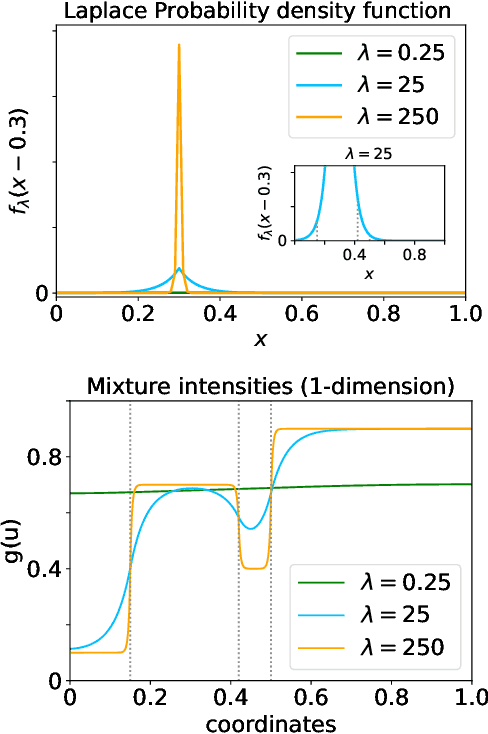
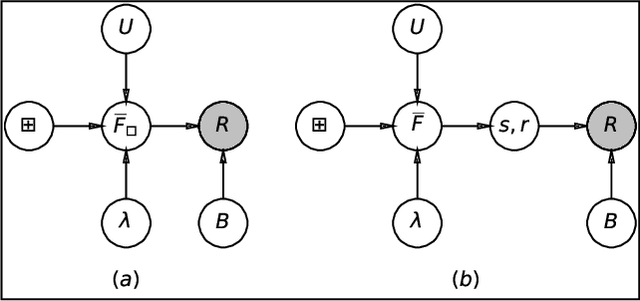
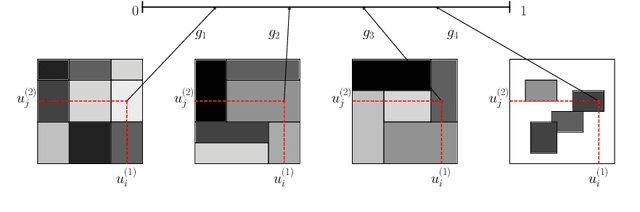
Modelling exchangeable relational data can be described by \textit{graphon theory}. Most Bayesian methods for modelling exchangeable relational data can be attributed to this framework by exploiting different forms of graphons. However, the graphons adopted by existing Bayesian methods are either piecewise-constant functions, which are insufficiently flexible for accurate modelling of the relational data, or are complicated continuous functions, which incur heavy computational costs for inference. In this work, we introduce a smoothing procedure to piecewise-constant graphons to form {\em smoothing graphons}, which permit continuous intensity values for describing relations, but without impractically increasing computational costs. In particular, we focus on the Bayesian Stochastic Block Model (SBM) and demonstrate how to adapt the piecewise-constant SBM graphon to the smoothed version. We initially propose the Integrated Smoothing Graphon (ISG) which introduces one smoothing parameter to the SBM graphon to generate continuous relational intensity values. We then develop the Latent Feature Smoothing Graphon (LFSG), which improves on the ISG by introducing auxiliary hidden labels to decompose the calculation of the ISG intensity and enable efficient inference. Experimental results on real-world data sets validate the advantages of applying smoothing strategies to the Stochastic Block Model, demonstrating that smoothing graphons can greatly improve AUC and precision for link prediction without increasing computational complexity.

Recurrent Dirichlet Belief Networks for Interpretable Dynamic Relational Data Modelling

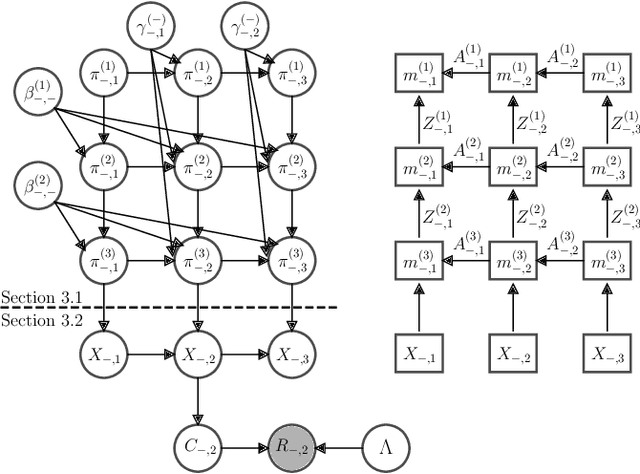
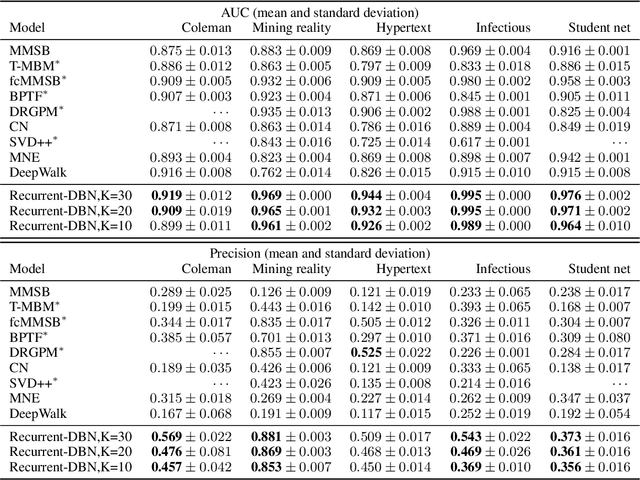
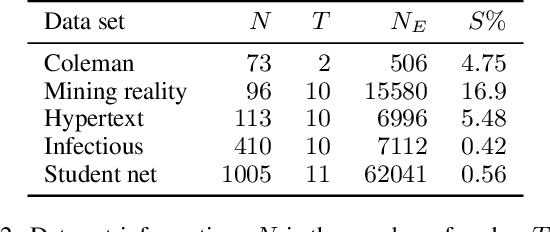
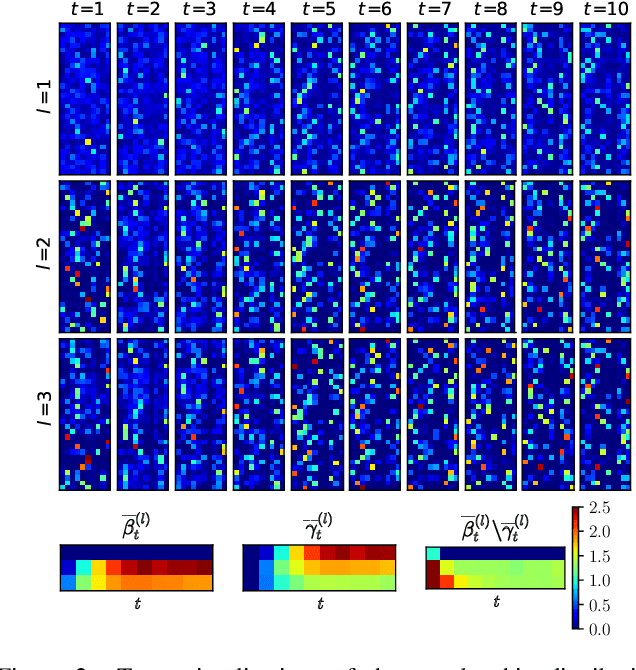
The Dirichlet Belief Network~(DirBN) has been recently proposed as a promising approach in learning interpretable deep latent representations for objects. In this work, we leverage its interpretable modelling architecture and propose a deep dynamic probabilistic framework -- the Recurrent Dirichlet Belief Network~(Recurrent-DBN) -- to study interpretable hidden structures from dynamic relational data. The proposed Recurrent-DBN has the following merits: (1) it infers interpretable and organised hierarchical latent structures for objects within and across time steps; (2) it enables recurrent long-term temporal dependence modelling, which outperforms the one-order Markov descriptions in most of the dynamic probabilistic frameworks. In addition, we develop a new inference strategy, which first upward-and-backward propagates latent counts and then downward-and-forward samples variables, to enable efficient Gibbs sampling for the Recurrent-DBN. We apply the Recurrent-DBN to dynamic relational data problems. The extensive experiment results on real-world data validate the advantages of the Recurrent-DBN over the state-of-the-art models in interpretable latent structure discovery and improved link prediction performance.

Logistic regression models for aggregated data

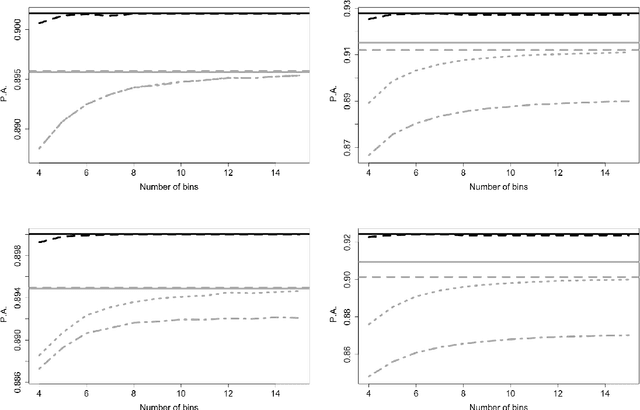
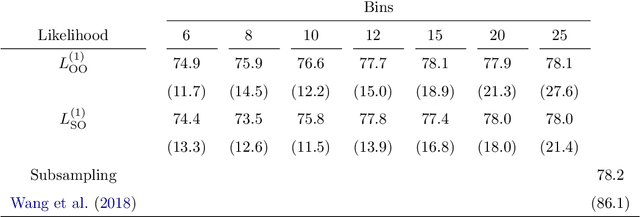
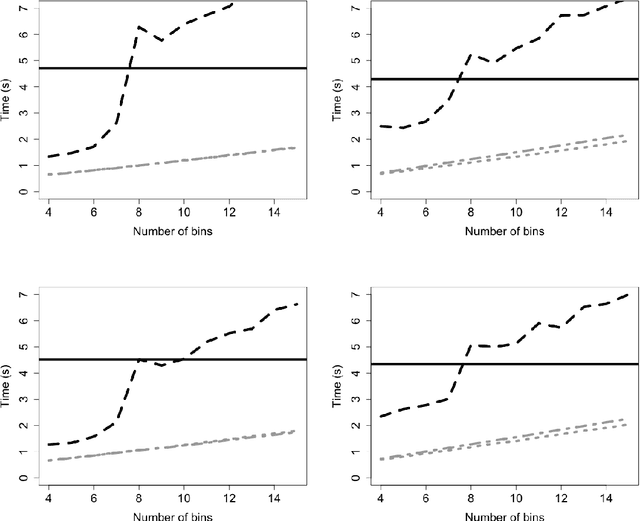
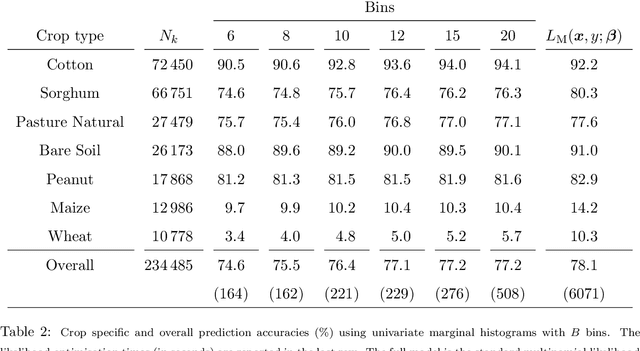
Logistic regression models are a popular and effective method to predict the probability of categorical response data. However inference for these models can become computationally prohibitive for large datasets. Here we adapt ideas from symbolic data analysis to summarise the collection of predictor variables into histogram form, and perform inference on this summary dataset. We develop ideas based on composite likelihoods to derive an efficient one-versus-rest approximate composite likelihood model for histogram-based random variables, constructed from low-dimensional marginal histograms obtained from the full histogram. We demonstrate that this procedure can achieve comparable classification rates compared to the standard full data multinomial analysis and against state-of-the-art subsampling algorithms for logistic regression, but at a substantially lower computational cost. Performance is explored through simulated examples, and analyses of large supersymmetry and satellite crop classification datasets.

Efficient Bayesian synthetic likelihood with whitening transformations

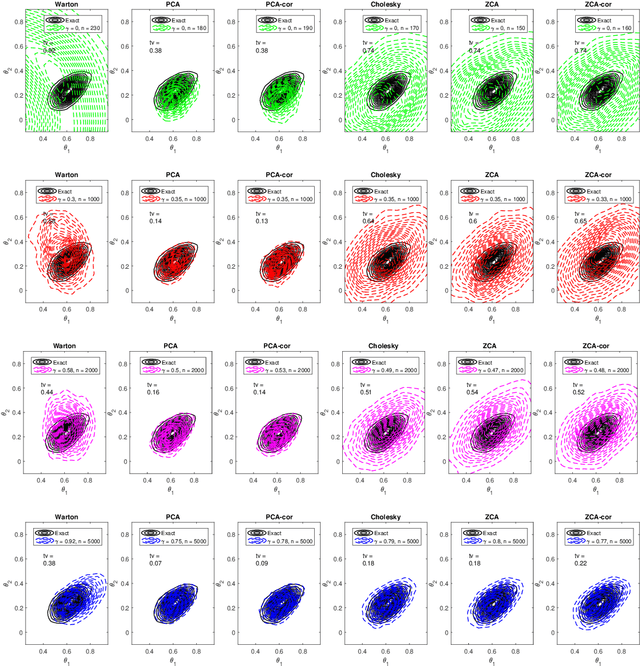
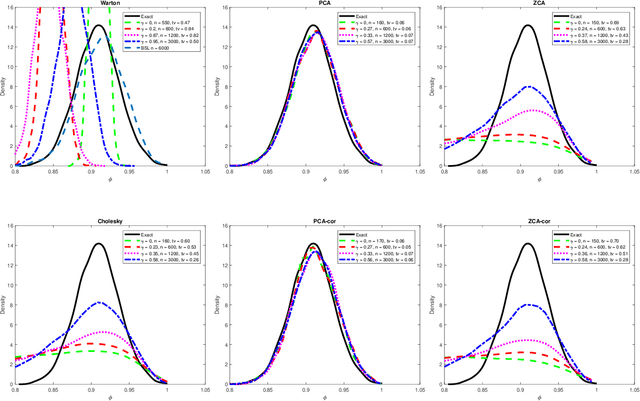
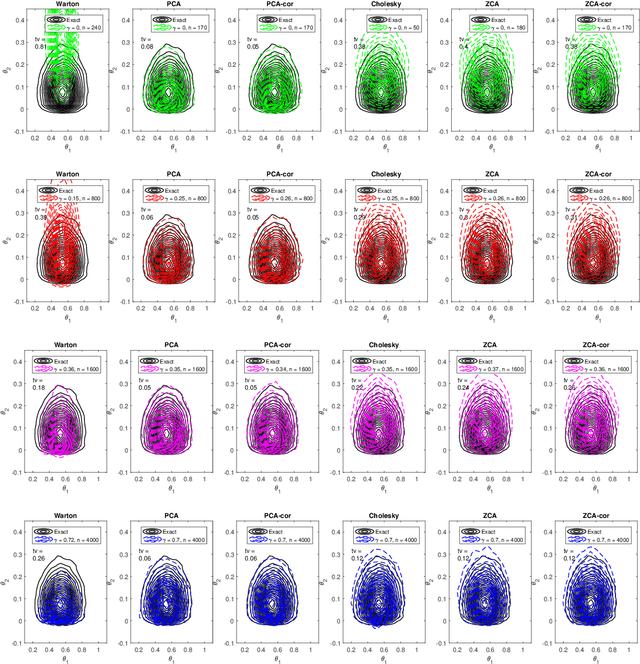
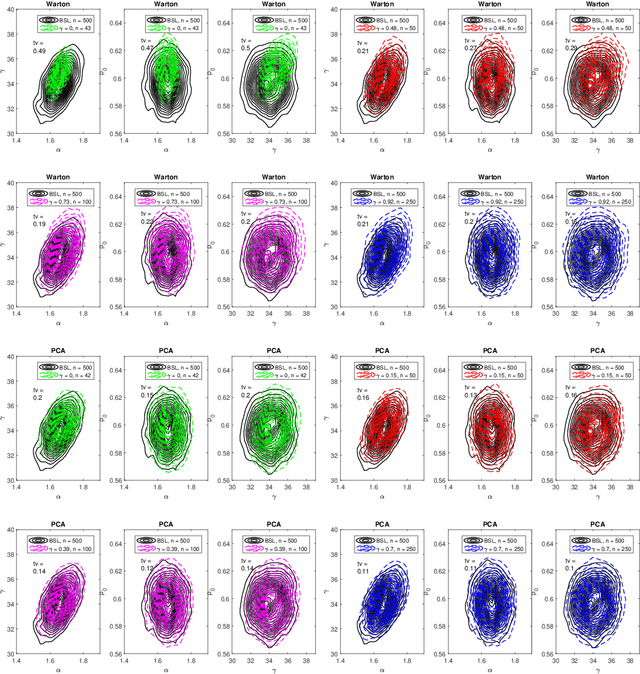
Likelihood-free methods are an established approach for performing approximate Bayesian inference for models with intractable likelihood functions. However, they can be computationally demanding. Bayesian synthetic likelihood (BSL) is a popular such method that approximates the likelihood function of the summary statistic with a known, tractable distribution -- typically Gaussian -- and then performs statistical inference using standard likelihood-based techniques. However, as the number of summary statistics grows, the number of model simulations required to accurately estimate the covariance matrix for this likelihood rapidly increases. This poses significant challenge for the application of BSL, especially in cases where model simulation is expensive. In this article we propose whitening BSL (wBSL) -- an efficient BSL method that uses approximate whitening transformations to decorrelate the summary statistics at each algorithm iteration. We show empirically that this can reduce the number of model simulations required to implement BSL by more than an order of magnitude, without much loss of accuracy. We explore a range of whitening procedures and demonstrate the performance of wBSL on a range of simulated and real modelling scenarios from ecology and biology.

Acceleration of expensive computations in Bayesian statistics using vector operations

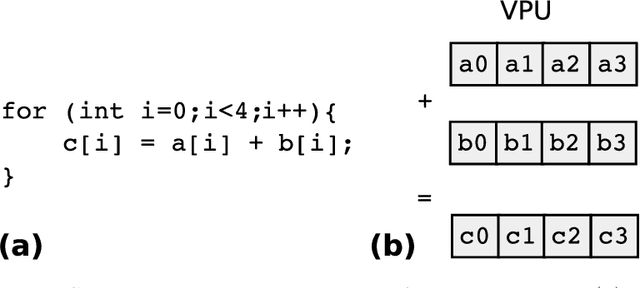
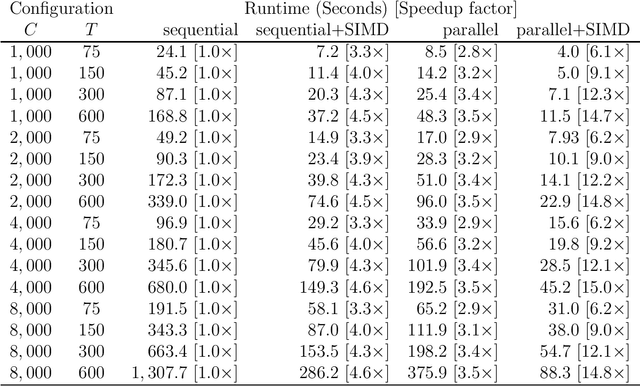
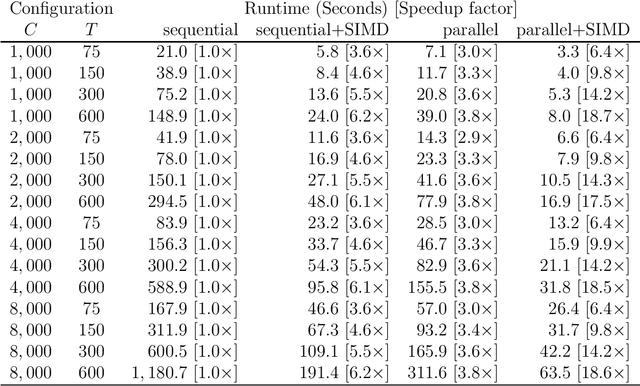
Many applications in Bayesian statistics are extremely computationally intensive. However, they are also often inherently parallel, making them prime targets for modern massively parallel central processing unit (CPU) architectures. While the use of multi-core and distributed computing is widely applied in the Bayesian community, very little attention has been given to fine-grain parallelisation using single instruction multiple data (SIMD) operations that are available on most modern commodity CPUs. Rather, most fine-grain tuning in the literature has centred around general purpose graphics processing units (GPGPUs). Since the effective utilisation of GPGPUs typically requires specialised programming languages, such technologies are not ideal for the wider Bayesian community. In this work, we practically demonstrate, using standard programming libraries, the utility of the SIMD approach for several topical Bayesian applications. In particular, we consider sampling of the prior predictive distribution for approximate Bayesian computation (ABC), and the computation of Bayesian $p$-values for testing prior weak informativeness. Through minor code alterations, we show that SIMD operations can improve the floating point arithmetic performance resulting in up to $6\times$ improvement in the overall serial algorithm performance. Furthermore $4$-way parallel versions can lead to almost $19\times$ improvement over a na\"{i}ve serial implementation. We illustrate the potential of SIMD operations for accelerating Bayesian computations and provide the reader with essential implementation techniques required to exploit modern massively parallel processing environments using standard software development tools.