Dendrograms of Mixing Measures for Softmax-Gated Gaussian Mixture of Experts: Consistency without Model Sweeps

We develop a unified statistical framework for softmax-gated Gaussian mixture of experts (SGMoE) that addresses three long-standing obstacles in parameter estimation and model selection: (i) non-identifiability of gating parameters up to common translations, (ii) intrinsic gate-expert interactions that induce coupled differential relations in the likelihood, and (iii) the tight numerator-denominator coupling in the softmax-induced conditional density. Our approach introduces Voronoi-type loss functions aligned with the gate-partition geometry and establishes finite-sample convergence rates for the maximum likelihood estimator (MLE). In over-specified models, we reveal a link between the MLE's convergence rate and the solvability of an associated system of polynomial equations characterizing near-nonidentifiable directions. For model selection, we adapt dendrograms of mixing measures to SGMoE, yielding a consistent, sweep-free selector of the number of experts that attains pointwise-optimal parameter rates under overfitting while avoiding multi-size training. Simulations on synthetic data corroborate the theory, accurately recovering the expert count and achieving the predicted rates for parameter estimation while closely approximating the regression function. Under model misspecification (e.g., $\epsilon$-contamination), the dendrogram selection criterion is robust, recovering the true number of mixture components, while the Akaike information criterion, the Bayesian information criterion, and the integrated completed likelihood tend to overselect as sample size grows. On a maize proteomics dataset of drought-responsive traits, our dendrogram-guided SGMoE selects two experts, exposes a clear mixing-measure hierarchy, stabilizes the likelihood early, and yields interpretable genotype-phenotype maps, outperforming standard criteria without multi-size training.

A Unified Framework for Variable Selection in Model-Based Clustering with Missing Not at Random

Model-based clustering integrated with variable selection is a powerful tool for uncovering latent structures within complex data. However, its effectiveness is often hindered by challenges such as identifying relevant variables that define heterogeneous subgroups and handling data that are missing not at random, a prevalent issue in fields like transcriptomics. While several notable methods have been proposed to address these problems, they typically tackle each issue in isolation, thereby limiting their flexibility and adaptability. This paper introduces a unified framework designed to address these challenges simultaneously. Our approach incorporates a data-driven penalty matrix into penalized clustering to enable more flexible variable selection, along with a mechanism that explicitly models the relationship between missingness and latent class membership. We demonstrate that, under certain regularity conditions, the proposed framework achieves both asymptotic consistency and selection consistency, even in the presence of missing data. This unified strategy significantly enhances the capability and efficiency of model-based clustering, advancing methodologies for identifying informative variables that define homogeneous subgroups in the presence of complex missing data patterns. The performance of the framework, including its computational efficiency, is evaluated through simulations and demonstrated using both synthetic and real-world transcriptomic datasets.

Model Selection for Gaussian-gated Gaussian Mixture of Experts Using Dendrograms of Mixing Measures

Mixture of Experts (MoE) models constitute a widely utilized class of ensemble learning approaches in statistics and machine learning, known for their flexibility and computational efficiency. They have become integral components in numerous state-of-the-art deep neural network architectures, particularly for analyzing heterogeneous data across diverse domains. Despite their practical success, the theoretical understanding of model selection, especially concerning the optimal number of mixture components or experts, remains limited and poses significant challenges. These challenges primarily stem from the inclusion of covariates in both the Gaussian gating functions and expert networks, which introduces intrinsic interactions governed by partial differential equations with respect to their parameters. In this paper, we revisit the concept of dendrograms of mixing measures and introduce a novel extension to Gaussian-gated Gaussian MoE models that enables consistent estimation of the true number of mixture components and achieves the pointwise optimal convergence rate for parameter estimation in overfitted scenarios. Notably, this approach circumvents the need to train and compare a range of models with varying numbers of components, thereby alleviating the computational burden, particularly in high-dimensional or deep neural network settings. Experimental results on synthetic data demonstrate the effectiveness of the proposed method in accurately recovering the number of experts. It outperforms common criteria such as the Akaike information criterion, the Bayesian information criterion, and the integrated completed likelihood, while achieving optimal convergence rates for parameter estimation and accurately approximating the regression function.

Simulation-based Bayesian inference under model misspecification

Simulation-based Bayesian inference (SBI) methods are widely used for parameter estimation in complex models where evaluating the likelihood is challenging but generating simulations is relatively straightforward. However, these methods commonly assume that the simulation model accurately reflects the true data-generating process, an assumption that is frequently violated in realistic scenarios. In this paper, we focus on the challenges faced by SBI methods under model misspecification. We consolidate recent research aimed at mitigating the effects of misspecification, highlighting three key strategies: i) robust summary statistics, ii) generalised Bayesian inference, and iii) error modelling and adjustment parameters. To illustrate both the vulnerabilities of popular SBI methods and the effectiveness of misspecification-robust alternatives, we present empirical results on an illustrative example.

The Polynomial Stein Discrepancy for Assessing Moment Convergence

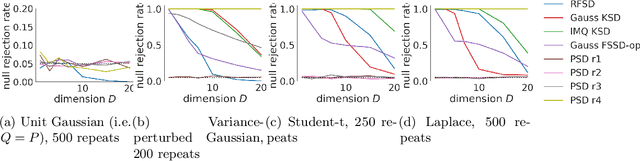
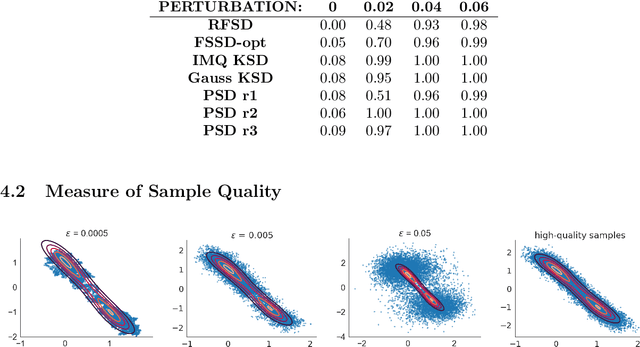
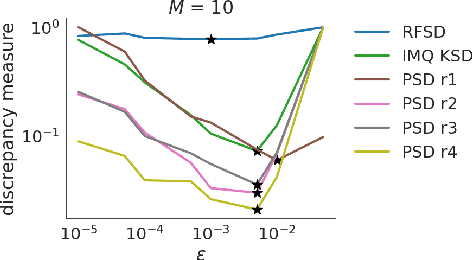
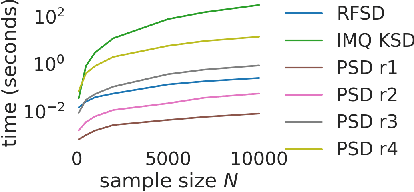
We propose a novel method for measuring the discrepancy between a set of samples and a desired posterior distribution for Bayesian inference. Classical methods for assessing sample quality like the effective sample size are not appropriate for scalable Bayesian sampling algorithms, such as stochastic gradient Langevin dynamics, that are asymptotically biased. Instead, the gold standard is to use the kernel Stein Discrepancy (KSD), which is itself not scalable given its quadratic cost in the number of samples. The KSD and its faster extensions also typically suffer from the curse-of-dimensionality and can require extensive tuning. To address these limitations, we develop the polynomial Stein discrepancy (PSD) and an associated goodness-of-fit test. While the new test is not fully convergence-determining, we prove that it detects differences in the first r moments in the Bernstein-von Mises limit. We empirically show that the test has higher power than its competitors in several examples, and at a lower computational cost. Finally, we demonstrate that the PSD can assist practitioners to select hyper-parameters of Bayesian sampling algorithms more efficiently than competitors.

The Statistical Accuracy of Neural Posterior and Likelihood Estimation

Neural posterior estimation (NPE) and neural likelihood estimation (NLE) are machine learning approaches that provide accurate posterior, and likelihood, approximations in complex modeling scenarios, and in situations where conducting amortized inference is a necessity. While such methods have shown significant promise across a range of diverse scientific applications, the statistical accuracy of these methods is so far unexplored. In this manuscript, we give, for the first time, an in-depth exploration on the statistical behavior of NPE and NLE. We prove that these methods have similar theoretical guarantees to common statistical methods like approximate Bayesian computation (ABC) and Bayesian synthetic likelihood (BSL). While NPE and NLE methods are just as accurate as ABC and BSL, we prove that this accuracy can often be achieved at a vastly reduced computational cost, and will therefore deliver more attractive approximations than ABC and BSL in certain problems. We verify our results theoretically and in several examples from the literature.

A Comprehensive Guide to Simulation-based Inference in Computational Biology

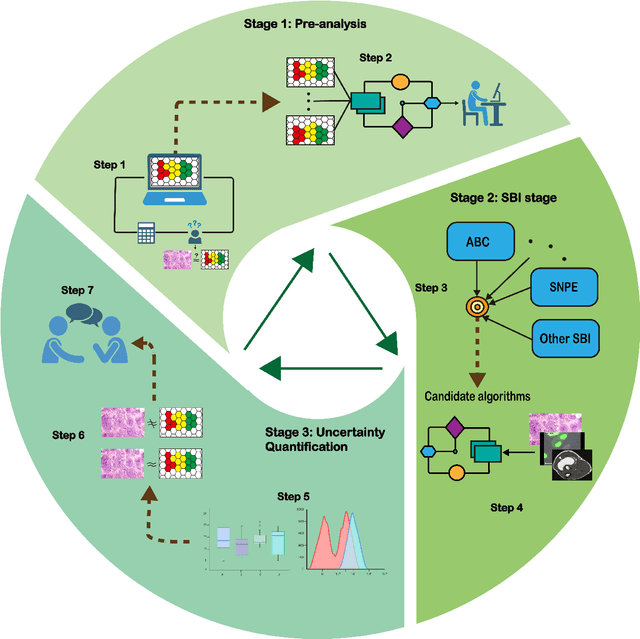
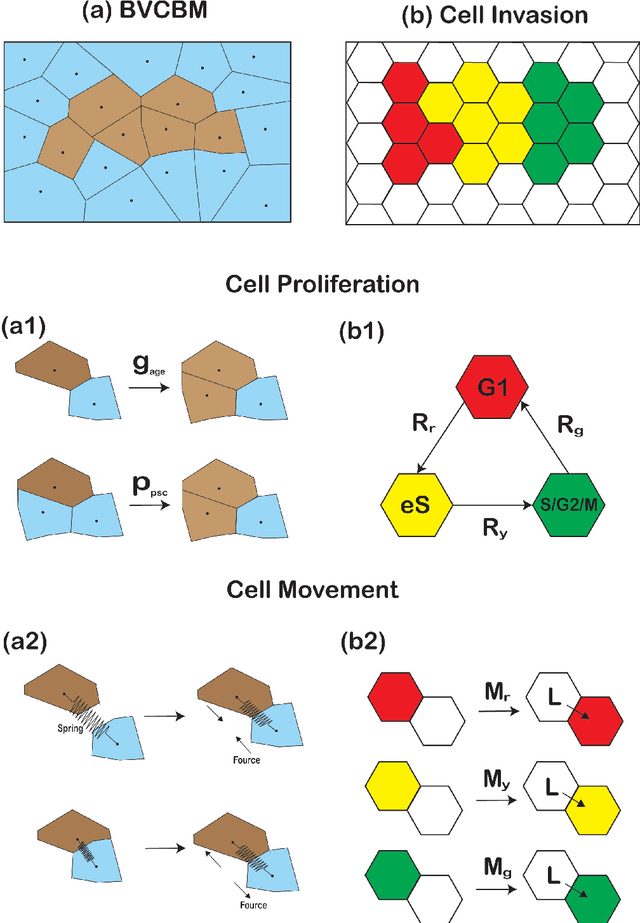
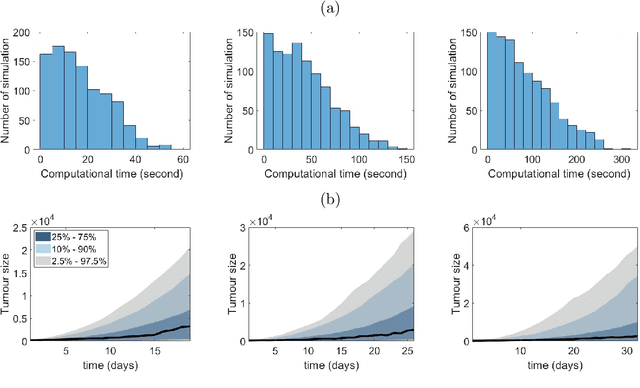
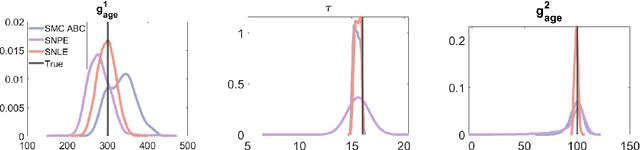
Computational models are invaluable in capturing the complexities of real-world biological processes. Yet, the selection of appropriate algorithms for inference tasks, especially when dealing with real-world observational data, remains a challenging and underexplored area. This gap has spurred the development of various parameter estimation algorithms, particularly within the realm of Simulation-Based Inference (SBI), such as neural and statistical SBI methods. Limited research exists on how to make informed choices on SBI methods when faced with real-world data, which often results in some form of model misspecification. In this paper, we provide comprehensive guidelines for deciding between SBI approaches for complex biological models. We apply the guidelines to two agent-based models that describe cellular dynamics using real-world data. Our study unveils a critical insight: while neural SBI methods demand significantly fewer simulations for inference results, they tend to yield biased estimations, a trend persistent even with robust variants of these algorithms. On the other hand, the accuracy of statistical SBI methods enhances substantially as the number of simulations increases. This finding suggests that, given a sufficient computational budget, statistical SBI can surpass neural SBI in performance. Our results not only shed light on the efficacy of different SBI methodologies in real-world scenarios but also suggest potential avenues for enhancing neural SBI approaches. This study is poised to be a useful resource for computational biologists navigating the intricate landscape of SBI in biological modeling.

Preconditioned Neural Posterior Estimation for Likelihood-free Inference

Simulation based inference (SBI) methods enable the estimation of posterior distributions when the likelihood function is intractable, but where model simulation is feasible. Popular neural approaches to SBI are the neural posterior estimator (NPE) and its sequential version (SNPE). These methods can outperform statistical SBI approaches such as approximate Bayesian computation (ABC), particularly for relatively small numbers of model simulations. However, we show in this paper that the NPE methods are not guaranteed to be highly accurate, even on problems with low dimension. In such settings the posterior cannot be accurately trained over the prior predictive space, and even the sequential extension remains sub-optimal. To overcome this, we propose preconditioned NPE (PNPE) and its sequential version (PSNPE), which uses a short run of ABC to effectively eliminate regions of parameter space that produce large discrepancy between simulations and data and allow the posterior emulator to be more accurately trained. We present comprehensive empirical evidence that this melding of neural and statistical SBI methods improves performance over a range of examples, including a motivating example involving a complex agent-based model applied to real tumour growth data.

Wasserstein Gaussianization and Efficient Variational Bayes for Robust Bayesian Synthetic Likelihood

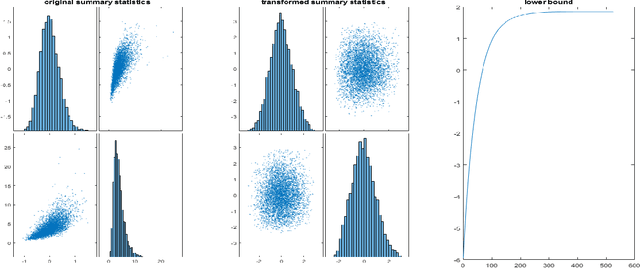
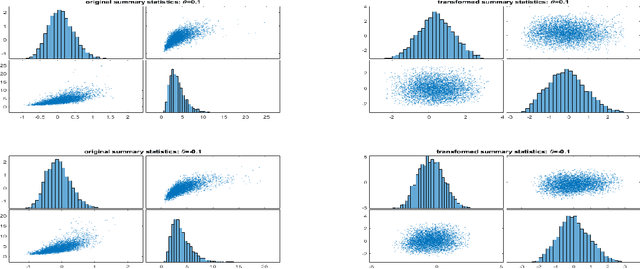
The Bayesian Synthetic Likelihood (BSL) method is a widely-used tool for likelihood-free Bayesian inference. This method assumes that some summary statistics are normally distributed, which can be incorrect in many applications. We propose a transformation, called the Wasserstein Gaussianization transformation, that uses a Wasserstein gradient flow to approximately transform the distribution of the summary statistics into a Gaussian distribution. BSL also implicitly requires compatibility between simulated summary statistics under the working model and the observed summary statistics. A robust BSL variant which achieves this has been developed in the recent literature. We combine the Wasserstein Gaussianization transformation with robust BSL, and an efficient Variational Bayes procedure for posterior approximation, to develop a highly efficient and reliable approximate Bayesian inference method for likelihood-free problems.

Bayesian score calibration for approximate models

Scientists continue to develop increasingly complex mechanistic models to reflect their knowledge more realistically. Statistical inference using these models can be highly challenging, since the corresponding likelihood function is often intractable, and model simulation may be computationally burdensome or infeasible. Fortunately, in many of these situations, it is possible to adopt a surrogate model or approximate likelihood function. It may be convenient to base Bayesian inference directly on the surrogate, but this can result in bias and poor uncertainty quantification. In this paper we propose a new method for adjusting approximate posterior samples to reduce bias and produce more accurate uncertainty quantification. We do this by optimising a transform of the approximate posterior that minimises a scoring rule. Our approach requires only a (fixed) small number of complex model simulations and is numerically stable. We demonstrate good performance of the new method on several examples of increasing complexity.