The Polynomial Stein Discrepancy for Assessing Moment Convergence

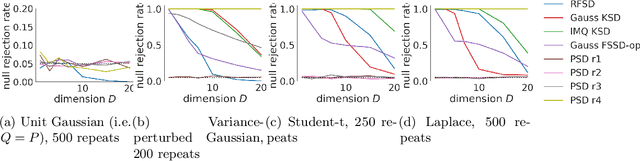
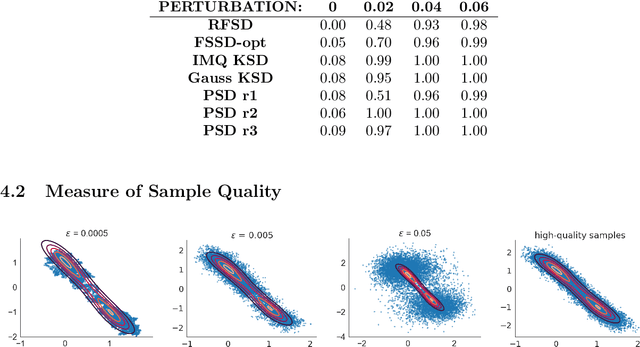
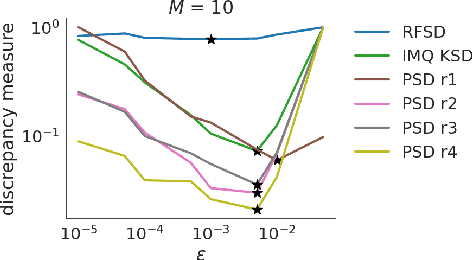
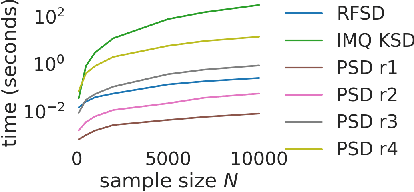
We propose a novel method for measuring the discrepancy between a set of samples and a desired posterior distribution for Bayesian inference. Classical methods for assessing sample quality like the effective sample size are not appropriate for scalable Bayesian sampling algorithms, such as stochastic gradient Langevin dynamics, that are asymptotically biased. Instead, the gold standard is to use the kernel Stein Discrepancy (KSD), which is itself not scalable given its quadratic cost in the number of samples. The KSD and its faster extensions also typically suffer from the curse-of-dimensionality and can require extensive tuning. To address these limitations, we develop the polynomial Stein discrepancy (PSD) and an associated goodness-of-fit test. While the new test is not fully convergence-determining, we prove that it detects differences in the first r moments in the Bernstein-von Mises limit. We empirically show that the test has higher power than its competitors in several examples, and at a lower computational cost. Finally, we demonstrate that the PSD can assist practitioners to select hyper-parameters of Bayesian sampling algorithms more efficiently than competitors.

BSL: An R Package for Efficient Parameter Estimation for Simulation-Based Models via Bayesian Synthetic Likelihood

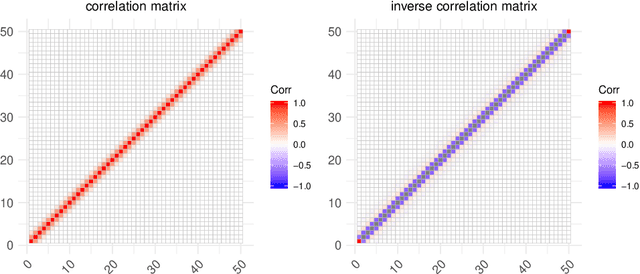
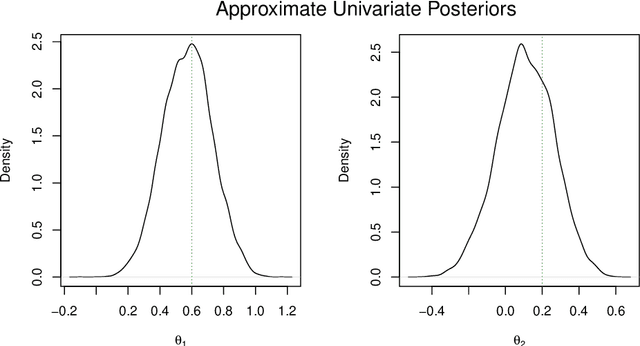
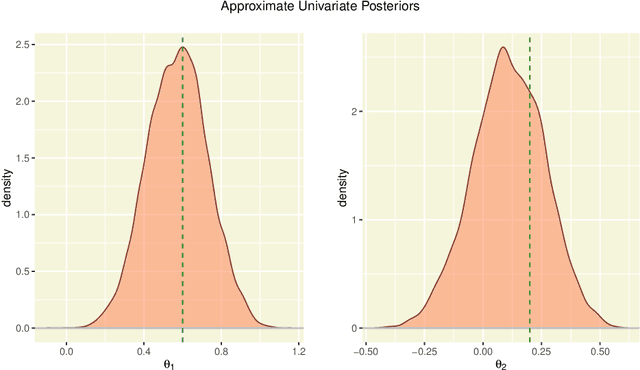
Bayesian synthetic likelihood (BSL) is a popular method for estimating the parameter posterior distribution for complex statistical models and stochastic processes that possess a computationally intractable likelihood function. Instead of evaluating the likelihood, BSL approximates the likelihood of a judiciously chosen summary statistic of the data via model simulation and density estimation. Compared to alternative methods such as approximate Bayesian computation (ABC), BSL requires little tuning and requires less model simulations than ABC when the chosen summary statistic is high-dimensional. The original synthetic likelihood relies on a multivariate normal approximation of the intractable likelihood, where the mean and covariance are estimated by simulation. An extension of BSL considers replacing the sample covariance with a penalised covariance estimator to reduce the number of required model simulations. Further, a semi-parametric approach has been developed to relax the normality assumption. In this paper, we present an R package called BSL that amalgamates the aforementioned methods and more into a single, easy-to-use and coherent piece of software. The R package also includes several examples to illustrate how to use the package and demonstrate the utility of the methods.