The Statistical Accuracy of Neural Posterior and Likelihood Estimation

Neural posterior estimation (NPE) and neural likelihood estimation (NLE) are machine learning approaches that provide accurate posterior, and likelihood, approximations in complex modeling scenarios, and in situations where conducting amortized inference is a necessity. While such methods have shown significant promise across a range of diverse scientific applications, the statistical accuracy of these methods is so far unexplored. In this manuscript, we give, for the first time, an in-depth exploration on the statistical behavior of NPE and NLE. We prove that these methods have similar theoretical guarantees to common statistical methods like approximate Bayesian computation (ABC) and Bayesian synthetic likelihood (BSL). While NPE and NLE methods are just as accurate as ABC and BSL, we prove that this accuracy can often be achieved at a vastly reduced computational cost, and will therefore deliver more attractive approximations than ABC and BSL in certain problems. We verify our results theoretically and in several examples from the literature.

A Comprehensive Guide to Simulation-based Inference in Computational Biology

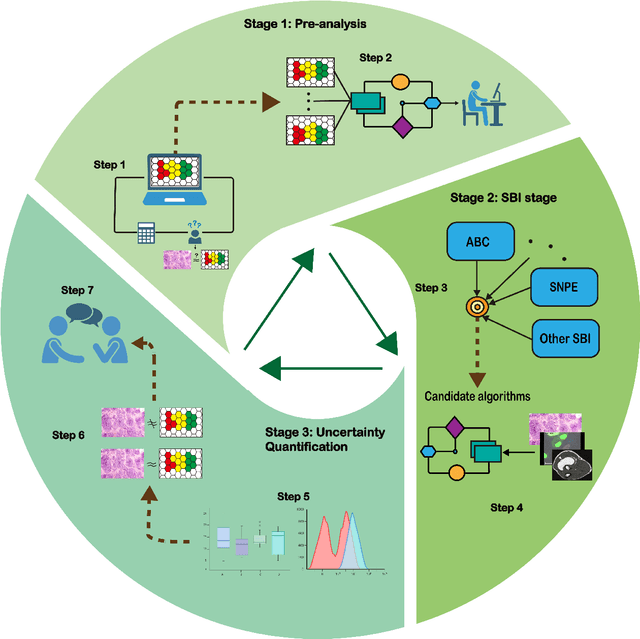
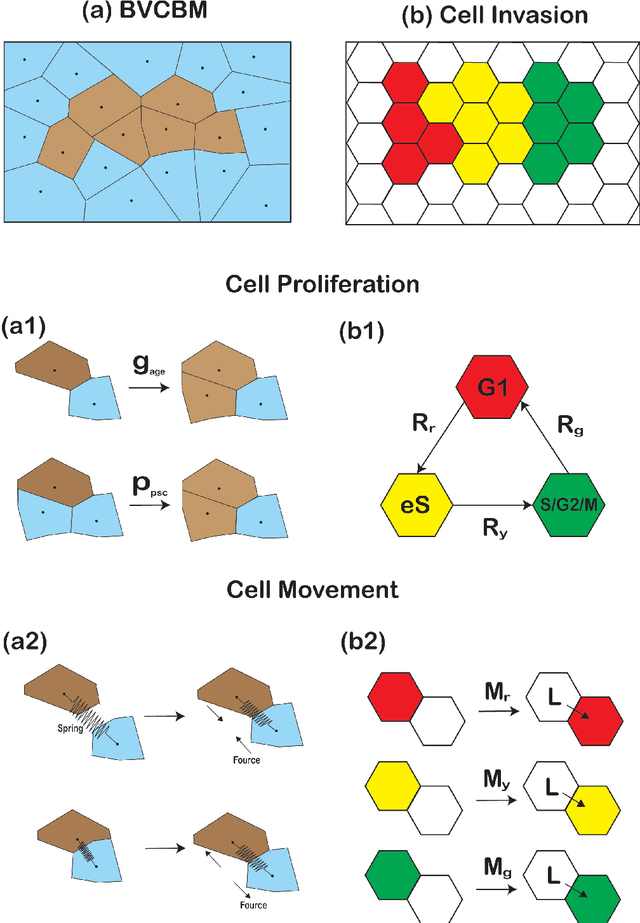
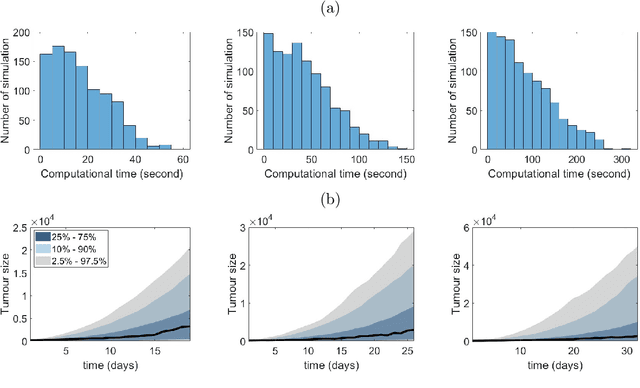
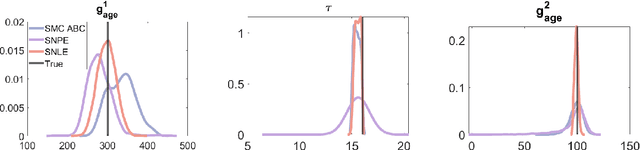
Computational models are invaluable in capturing the complexities of real-world biological processes. Yet, the selection of appropriate algorithms for inference tasks, especially when dealing with real-world observational data, remains a challenging and underexplored area. This gap has spurred the development of various parameter estimation algorithms, particularly within the realm of Simulation-Based Inference (SBI), such as neural and statistical SBI methods. Limited research exists on how to make informed choices on SBI methods when faced with real-world data, which often results in some form of model misspecification. In this paper, we provide comprehensive guidelines for deciding between SBI approaches for complex biological models. We apply the guidelines to two agent-based models that describe cellular dynamics using real-world data. Our study unveils a critical insight: while neural SBI methods demand significantly fewer simulations for inference results, they tend to yield biased estimations, a trend persistent even with robust variants of these algorithms. On the other hand, the accuracy of statistical SBI methods enhances substantially as the number of simulations increases. This finding suggests that, given a sufficient computational budget, statistical SBI can surpass neural SBI in performance. Our results not only shed light on the efficacy of different SBI methodologies in real-world scenarios but also suggest potential avenues for enhancing neural SBI approaches. This study is poised to be a useful resource for computational biologists navigating the intricate landscape of SBI in biological modeling.

Preconditioned Neural Posterior Estimation for Likelihood-free Inference

Simulation based inference (SBI) methods enable the estimation of posterior distributions when the likelihood function is intractable, but where model simulation is feasible. Popular neural approaches to SBI are the neural posterior estimator (NPE) and its sequential version (SNPE). These methods can outperform statistical SBI approaches such as approximate Bayesian computation (ABC), particularly for relatively small numbers of model simulations. However, we show in this paper that the NPE methods are not guaranteed to be highly accurate, even on problems with low dimension. In such settings the posterior cannot be accurately trained over the prior predictive space, and even the sequential extension remains sub-optimal. To overcome this, we propose preconditioned NPE (PNPE) and its sequential version (PSNPE), which uses a short run of ABC to effectively eliminate regions of parameter space that produce large discrepancy between simulations and data and allow the posterior emulator to be more accurately trained. We present comprehensive empirical evidence that this melding of neural and statistical SBI methods improves performance over a range of examples, including a motivating example involving a complex agent-based model applied to real tumour growth data.

Misspecification-robust Sequential Neural Likelihood

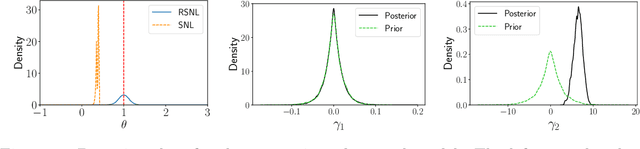
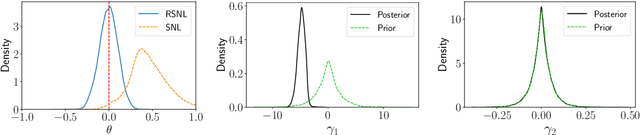
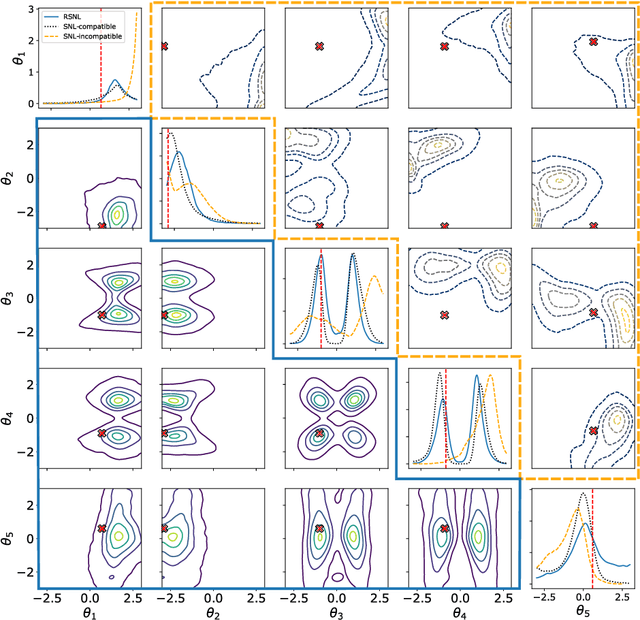
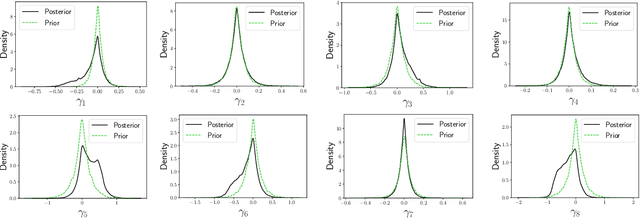
Simulation-based inference (SBI) techniques are now an essential tool for the parameter estimation of mechanistic and simulatable models with intractable likelihoods. Statistical approaches to SBI such as approximate Bayesian computation and Bayesian synthetic likelihood have been well studied in the well specified and misspecified settings. However, most implementations are inefficient in that many model simulations are wasted. Neural approaches such as sequential neural likelihood (SNL) have been developed that exploit all model simulations to build a surrogate of the likelihood function. However, SNL approaches have been shown to perform poorly under model misspecification. In this paper, we develop a new method for SNL that is robust to model misspecification and can identify areas where the model is deficient. We demonstrate the usefulness of the new approach on several illustrative examples.

Acceleration of expensive computations in Bayesian statistics using vector operations

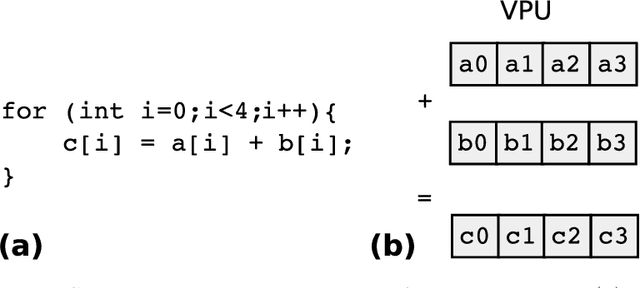
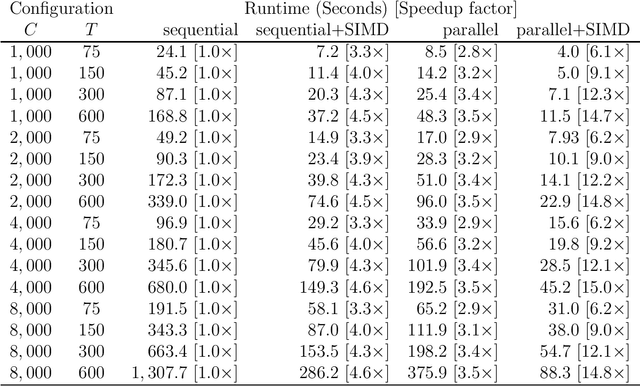
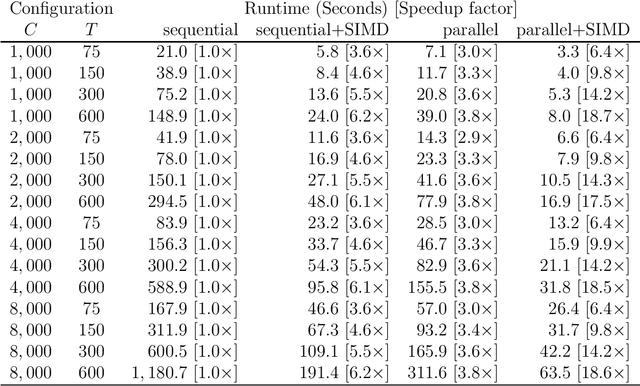
Many applications in Bayesian statistics are extremely computationally intensive. However, they are also often inherently parallel, making them prime targets for modern massively parallel central processing unit (CPU) architectures. While the use of multi-core and distributed computing is widely applied in the Bayesian community, very little attention has been given to fine-grain parallelisation using single instruction multiple data (SIMD) operations that are available on most modern commodity CPUs. Rather, most fine-grain tuning in the literature has centred around general purpose graphics processing units (GPGPUs). Since the effective utilisation of GPGPUs typically requires specialised programming languages, such technologies are not ideal for the wider Bayesian community. In this work, we practically demonstrate, using standard programming libraries, the utility of the SIMD approach for several topical Bayesian applications. In particular, we consider sampling of the prior predictive distribution for approximate Bayesian computation (ABC), and the computation of Bayesian $p$-values for testing prior weak informativeness. Through minor code alterations, we show that SIMD operations can improve the floating point arithmetic performance resulting in up to $6\times$ improvement in the overall serial algorithm performance. Furthermore $4$-way parallel versions can lead to almost $19\times$ improvement over a na\"{i}ve serial implementation. We illustrate the potential of SIMD operations for accelerating Bayesian computations and provide the reader with essential implementation techniques required to exploit modern massively parallel processing environments using standard software development tools.