Simulation-based Bayesian inference under model misspecification

Simulation-based Bayesian inference (SBI) methods are widely used for parameter estimation in complex models where evaluating the likelihood is challenging but generating simulations is relatively straightforward. However, these methods commonly assume that the simulation model accurately reflects the true data-generating process, an assumption that is frequently violated in realistic scenarios. In this paper, we focus on the challenges faced by SBI methods under model misspecification. We consolidate recent research aimed at mitigating the effects of misspecification, highlighting three key strategies: i) robust summary statistics, ii) generalised Bayesian inference, and iii) error modelling and adjustment parameters. To illustrate both the vulnerabilities of popular SBI methods and the effectiveness of misspecification-robust alternatives, we present empirical results on an illustrative example.

Positional Encoder Graph Quantile Neural Networks for Geographic Data

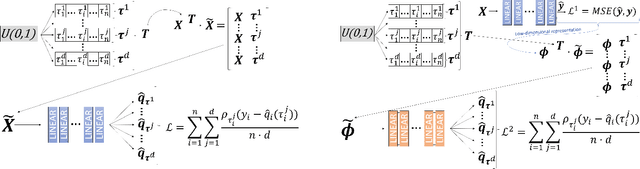
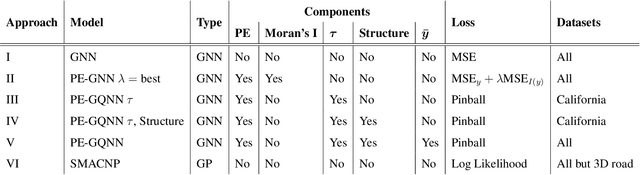
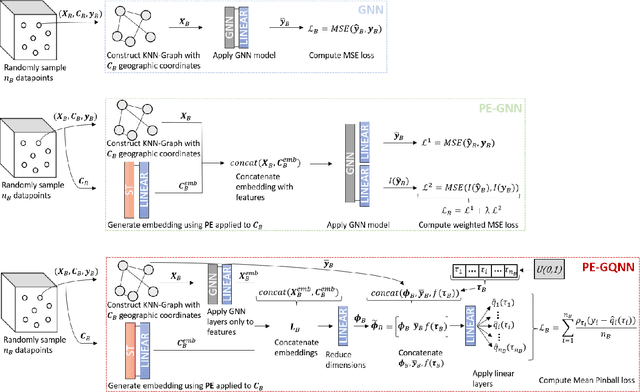
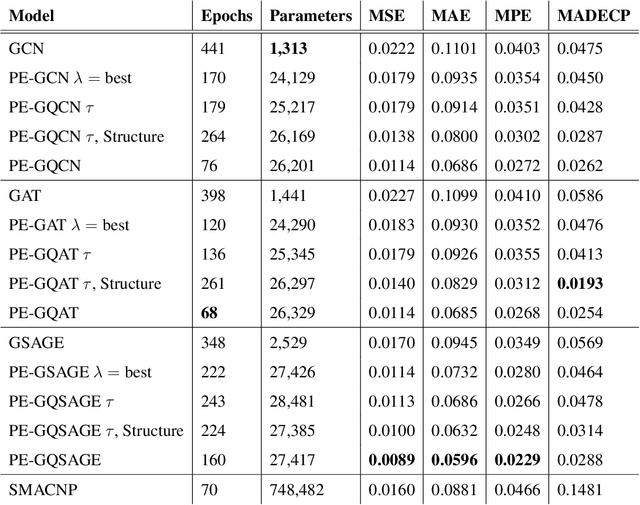
Positional Encoder Graph Neural Networks (PE-GNNs) are a leading approach for modeling continuous spatial data. However, they often fail to produce calibrated predictive distributions, limiting their effectiveness for uncertainty quantification. We introduce the Positional Encoder Graph Quantile Neural Network (PE-GQNN), a novel method that integrates PE-GNNs, Quantile Neural Networks, and recalibration techniques in a fully nonparametric framework, requiring minimal assumptions about the predictive distributions. We propose a new network architecture that, when combined with a quantile-based loss function, yields accurate and reliable probabilistic models without increasing computational complexity. Our approach provides a flexible, robust framework for conditional density estimation, applicable beyond spatial data contexts. We further introduce a structured method for incorporating a KNN predictor into the model while avoiding data leakage through the GNN layer operation. Experiments on benchmark datasets demonstrate that PE-GQNN significantly outperforms existing state-of-the-art methods in both predictive accuracy and uncertainty quantification.

Dropout Regularization in Extended Generalized Linear Models based on Double Exponential Families

Even though dropout is a popular regularization technique, its theoretical properties are not fully understood. In this paper we study dropout regularization in extended generalized linear models based on double exponential families, for which the dispersion parameter can vary with the features. A theoretical analysis shows that dropout regularization prefers rare but important features in both the mean and dispersion, generalizing an earlier result for conventional generalized linear models. Training is performed using stochastic gradient descent with adaptive learning rate. To illustrate, we apply dropout to adaptive smoothing with B-splines, where both the mean and dispersion parameters are modelled flexibly. The important B-spline basis functions can be thought of as rare features, and we confirm in experiments that dropout is an effective form of regularization for mean and dispersion parameters that improves on a penalized maximum likelihood approach with an explicit smoothness penalty.

Misspecification-robust Sequential Neural Likelihood

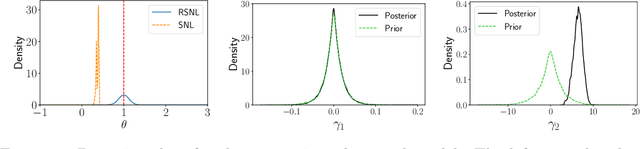
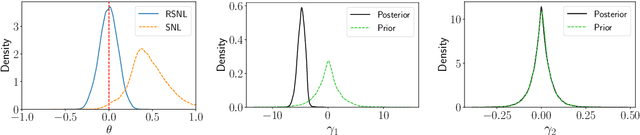
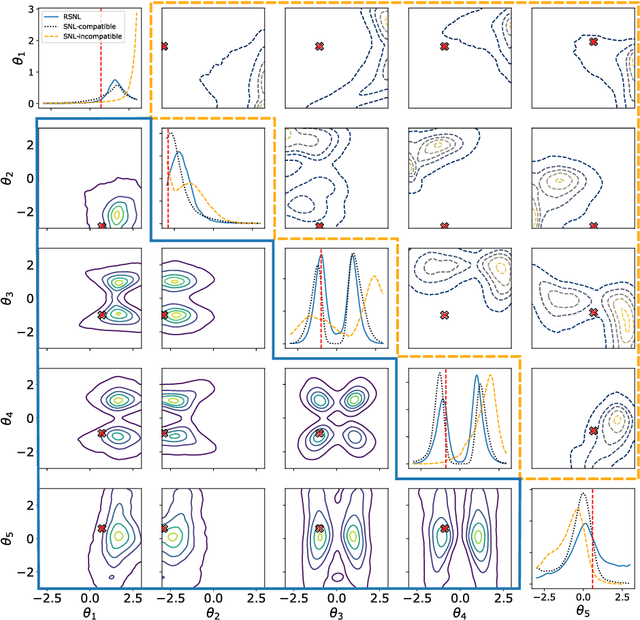
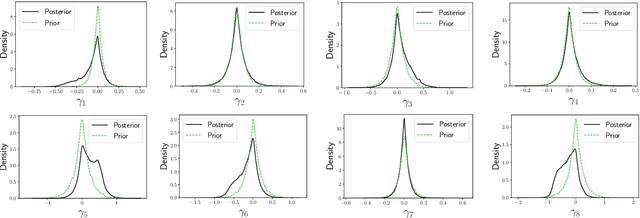
Simulation-based inference (SBI) techniques are now an essential tool for the parameter estimation of mechanistic and simulatable models with intractable likelihoods. Statistical approaches to SBI such as approximate Bayesian computation and Bayesian synthetic likelihood have been well studied in the well specified and misspecified settings. However, most implementations are inefficient in that many model simulations are wasted. Neural approaches such as sequential neural likelihood (SNL) have been developed that exploit all model simulations to build a surrogate of the likelihood function. However, SNL approaches have been shown to perform poorly under model misspecification. In this paper, we develop a new method for SNL that is robust to model misspecification and can identify areas where the model is deficient. We demonstrate the usefulness of the new approach on several illustrative examples.

On a Variational Approximation based Empirical Likelihood ABC Method

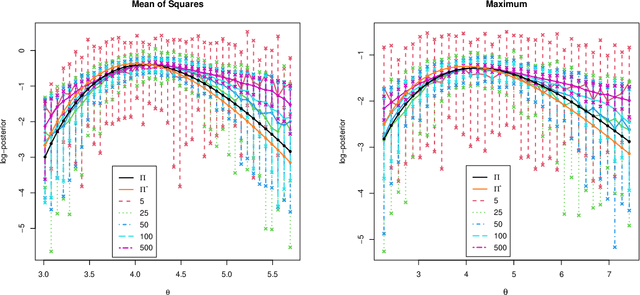
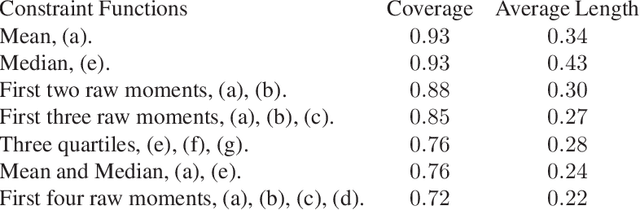
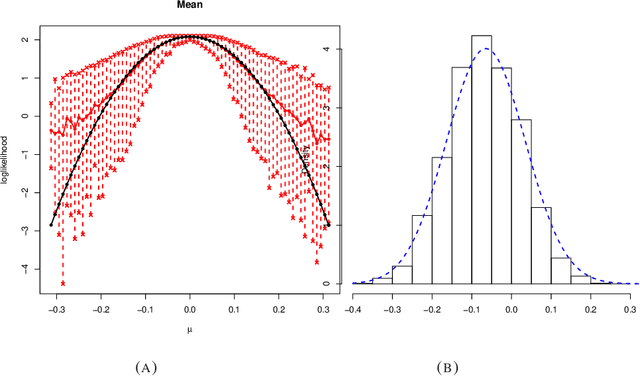
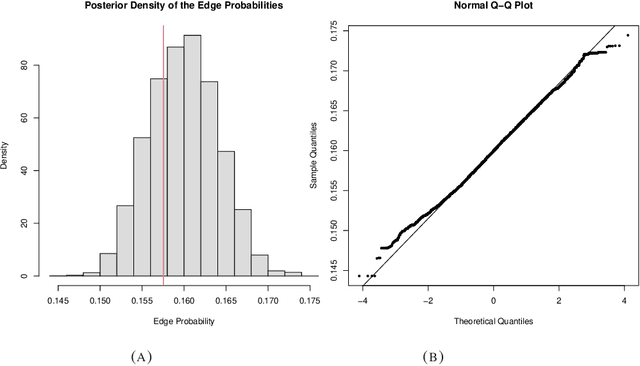
Many scientifically well-motivated statistical models in natural, engineering, and environmental sciences are specified through a generative process. However, in some cases, it may not be possible to write down the likelihood for these models analytically. Approximate Bayesian computation (ABC) methods allow Bayesian inference in such situations. The procedures are nonetheless typically computationally intensive. Recently, computationally attractive empirical likelihood-based ABC methods have been suggested in the literature. All of these methods rely on the availability of several suitable analytically tractable estimating equations, and this is sometimes problematic. We propose an easy-to-use empirical likelihood ABC method in this article. First, by using a variational approximation argument as a motivation, we show that the target log-posterior can be approximated as a sum of an expected joint log-likelihood and the differential entropy of the data generating density. The expected log-likelihood is then estimated by an empirical likelihood where the only inputs required are a choice of summary statistic, it's observed value, and the ability to simulate the chosen summary statistics for any parameter value under the model. The differential entropy is estimated from the simulated summaries using traditional methods. Posterior consistency is established for the method, and we discuss the bounds for the required number of simulated summaries in detail. The performance of the proposed method is explored in various examples.

Deep Distributional Time Series Models and the Probabilistic Forecasting of Intraday Electricity Prices

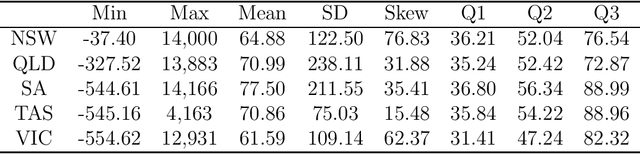
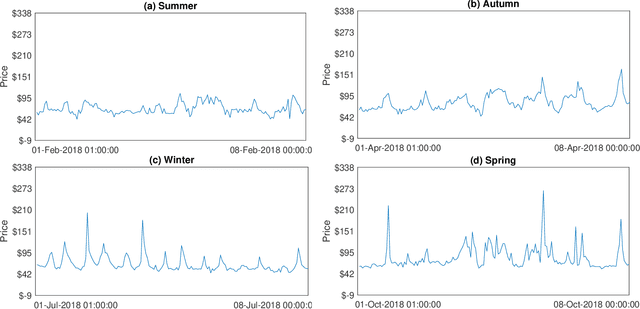
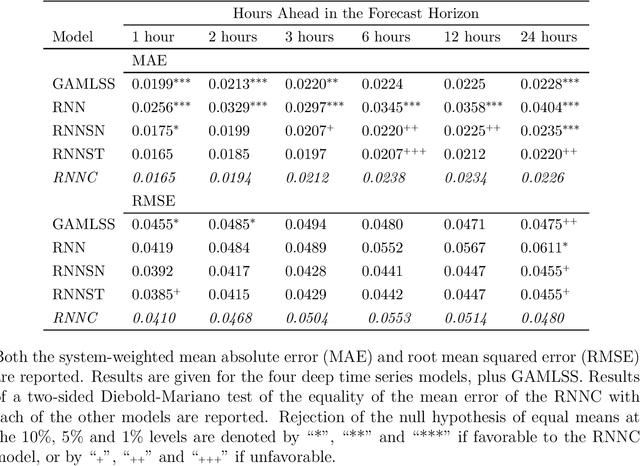
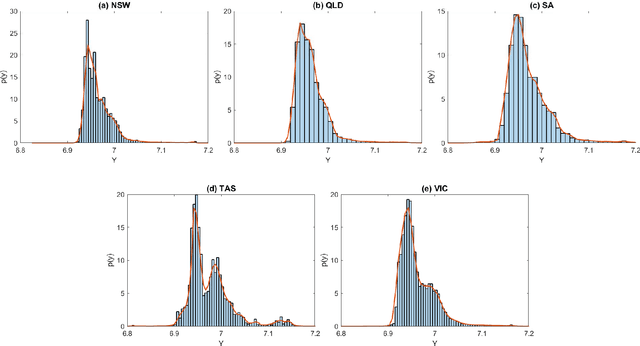
Recurrent neural networks (RNNs) with rich feature vectors of past values can provide accurate point forecasts for series that exhibit complex serial dependence. We propose two approaches to constructing deep time series probabilistic models based on a variant of RNN called an echo state network (ESN). The first is where the output layer of the ESN has stochastic disturbances and a shrinkage prior for additional regularization. The second approach employs the implicit copula of an ESN with Gaussian disturbances, which is a deep copula process on the feature space. Combining this copula with a non-parametrically estimated marginal distribution produces a deep distributional time series model. The resulting probabilistic forecasts are deep functions of the feature vector and also marginally calibrated. In both approaches, Bayesian Markov chain Monte Carlo methods are used to estimate the models and compute forecasts. The proposed deep time series models are suitable for the complex task of forecasting intraday electricity prices. Using data from the Australian National Electricity Market, we show that our models provide accurate probabilistic price forecasts. Moreover, the models provide a flexible framework for incorporating probabilistic forecasts of electricity demand as additional features. We demonstrate that doing so in the deep distributional time series model in particular, increases price forecast accuracy substantially.

Marginally-calibrated deep distributional regression

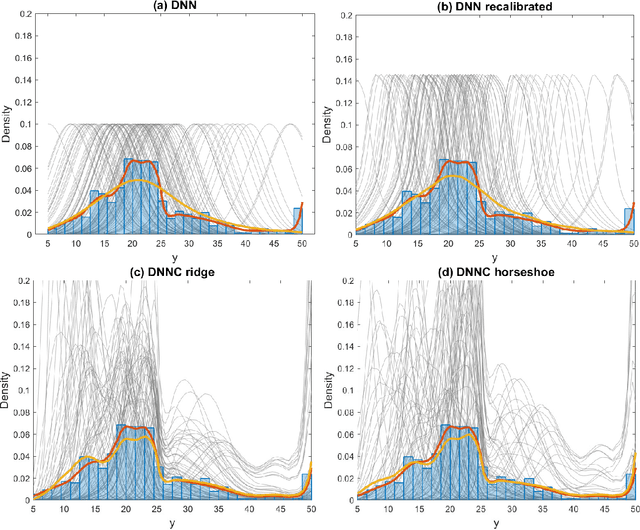
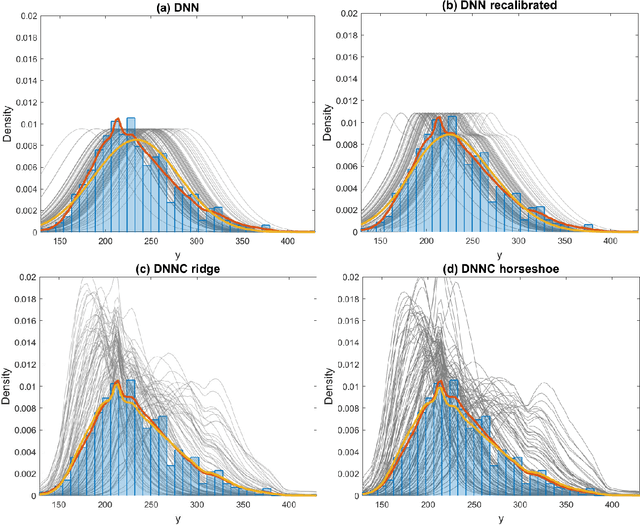
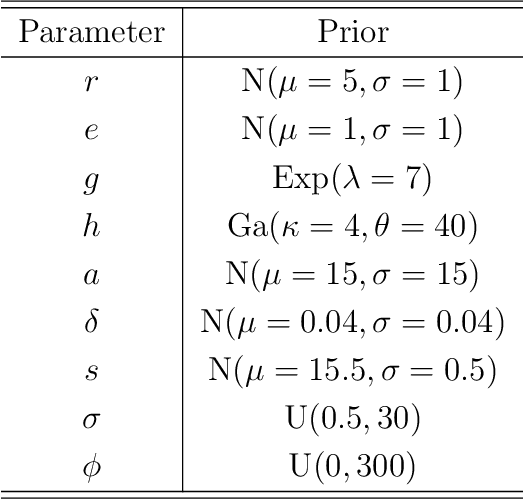
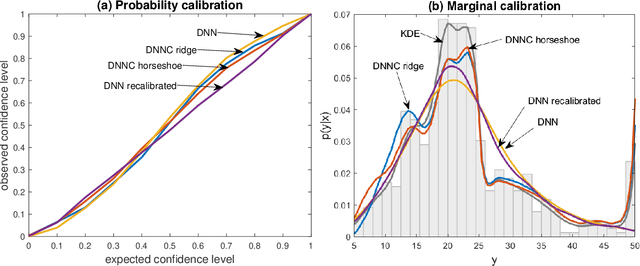
Deep neural network (DNN) regression models are widely used in applications requiring state-of-the-art predictive accuracy. However, until recently there has been little work on accurate uncertainty quantification for predictions from such models. We add to this literature by outlining an approach to constructing predictive distributions that are `marginally calibrated'. This is where the long run average of the predictive distributions of the response variable matches the observed empirical margin. Our approach considers a DNN regression with a conditionally Gaussian prior for the final layer weights, from which an implicit copula process on the feature space is extracted. This copula process is combined with a non-parametrically estimated marginal distribution for the response. The end result is a scalable distributional DNN regression method with marginally calibrated predictions, and our work complements existing methods for probability calibration. The approach is first illustrated using two applications of dense layer feed-forward neural networks. However, our main motivating applications are in likelihood-free inference, where distributional deep regression is used to estimate marginal posterior distributions. In two complex ecological time series examples we employ the implicit copulas of convolutional networks, and show that marginal calibration results in improved uncertainty quantification. Our approach also avoids the need for manual specification of summary statistics, a requirement that is burdensome for users and typical of competing likelihood-free inference methods.

An easy-to-use empirical likelihood ABC method

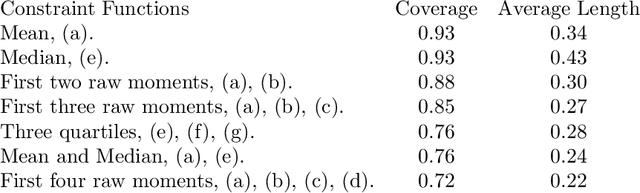
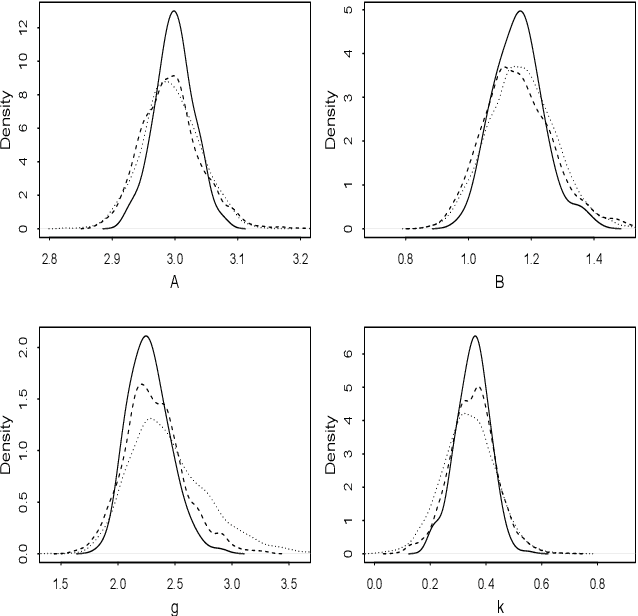
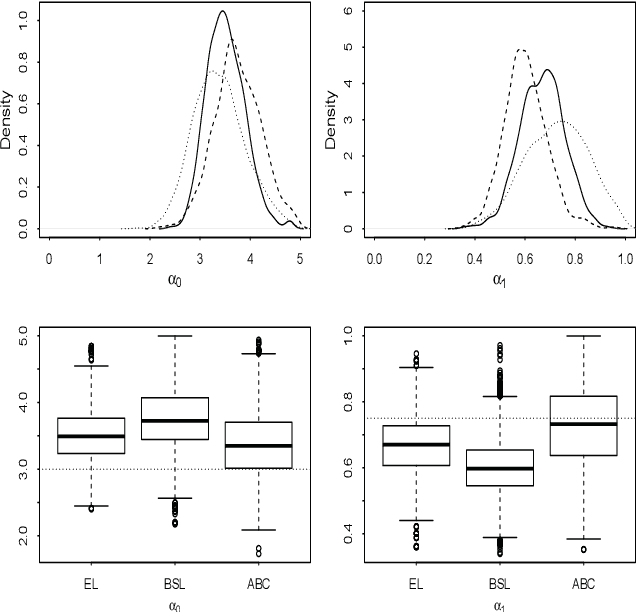
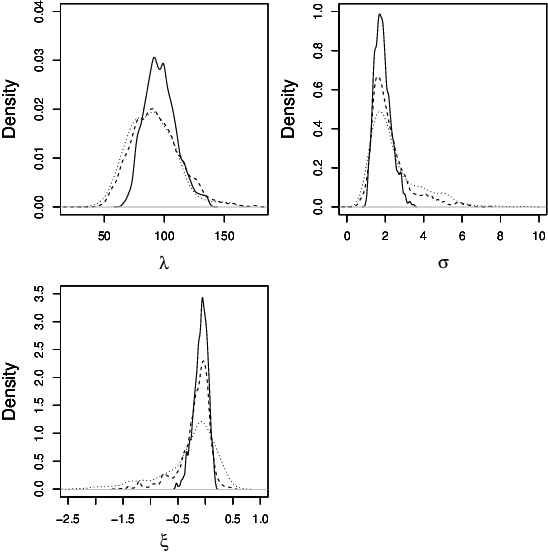
Many scientifically well-motivated statistical models in natural, engineering and environmental sciences are specified through a generative process, but in some cases it may not be possible to write down a likelihood for these models analytically. Approximate Bayesian computation (ABC) methods, which allow Bayesian inference in these situations, are typically computationally intensive. Recently, computationally attractive empirical likelihood based ABC methods have been suggested in the literature. These methods heavily rely on the availability of a set of suitable analytically tractable estimating equations. We propose an easy-to-use empirical likelihood ABC method, where the only inputs required are a choice of summary statistic, it's observed value, and the ability to simulate summary statistics for any parameter value under the model. It is shown that the posterior obtained using the proposed method is consistent, and its performance is explored using various examples.

Gaussian variational approximation for high-dimensional state space models

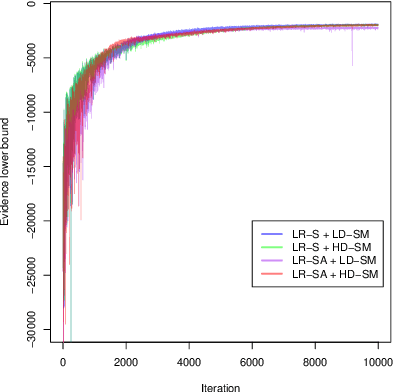
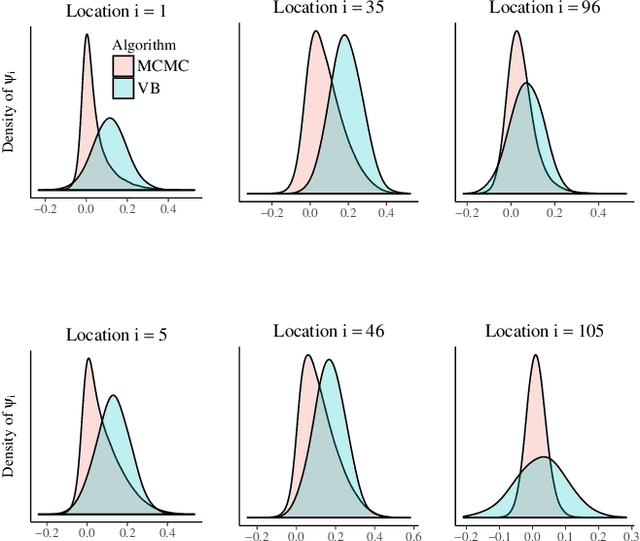
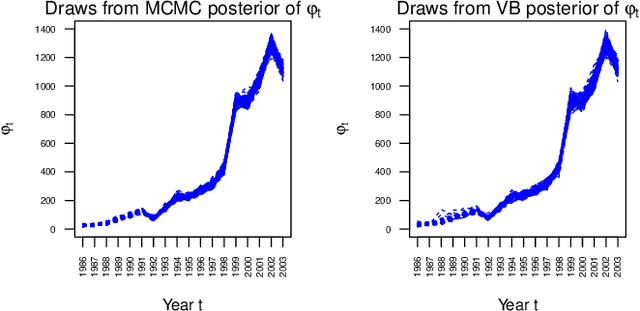
This article considers variational approximations of the posterior distribution in a high-dimensional state space model. The variational approximation is a multivariate Gaussian density, in which the variational parameters to be optimized are a mean vector and a covariance matrix. The number of parameters in the covariance matrix grows as the square of the number of model parameters, so it is necessary to find simple yet effective parametrizations of the covariance structure when the number of model parameters is large. The joint posterior distribution over the high-dimensional state vectors is approximated using a dynamic factor model, with Markovian dependence in time and a factor covariance structure for the states. This gives a reduced dimension description of the dependence structure for the states, as well as a temporal conditional independence structure similar to that in the true posterior. We illustrate our approach in two high-dimensional applications which are challenging for Markov chain Monte Carlo sampling. The first is a spatio-temporal model for the spread of the Eurasian Collared-Dove across North America. The second is a multivariate stochastic volatility model for financial returns via a Wishart process.

Gaussian variational approximation with sparse precision matrices

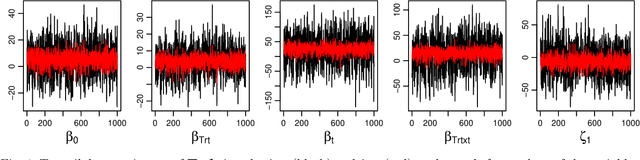
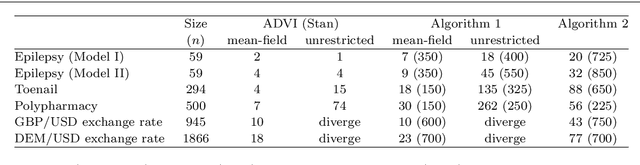
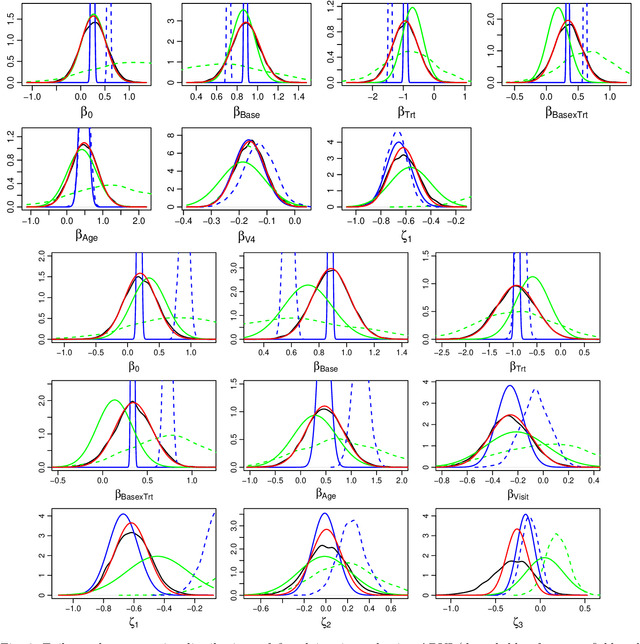
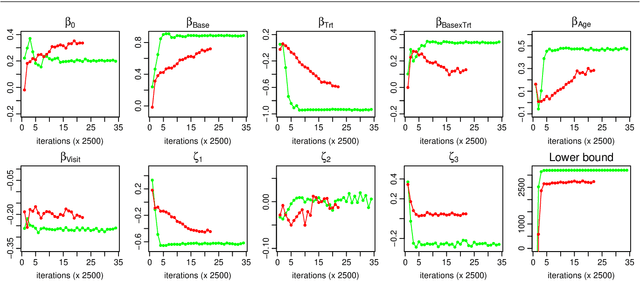
We consider the problem of learning a Gaussian variational approximation to the posterior distribution for a high-dimensional parameter, where we impose sparsity in the precision matrix to reflect appropriate conditional independence structure in the model. Incorporating sparsity in the precision matrix allows the Gaussian variational distribution to be both flexible and parsimonious, and the sparsity is achieved through parameterization in terms of the Cholesky factor. Efficient stochastic gradient methods which make appropriate use of gradient information for the target distribution are developed for the optimization. We consider alternative estimators of the stochastic gradients which have lower variation and are more stable. Our approach is illustrated using generalized linear mixed models and state space models for time series.