Efficient Variational Inference for Large Skew-t Copulas with Application to Intraday Equity Returns

Large skew-t factor copula models are attractive for the modeling of financial data because they allow for asymmetric and extreme tail dependence. We show that the copula implicit in the skew-t distribution of Azzalini and Capitanio (2003) allows for a higher level of pairwise asymmetric dependence than two popular alternative skew-t copulas. Estimation of this copula in high dimensions is challenging, and we propose a fast and accurate Bayesian variational inference (VI) approach to do so. The method uses a conditionally Gaussian generative representation of the skew-t distribution to define an augmented posterior that can be approximated accurately. A fast stochastic gradient ascent algorithm is used to solve the variational optimization. The new methodology is used to estimate copula models for intraday returns from 2017 to 2021 on 93 U.S. equities. The copula captures substantial heterogeneity in asymmetric dependence over equity pairs, in addition to the variability in pairwise correlations. We show that intraday predictive densities from the skew-t copula are more accurate than from some other copula models, while portfolio selection strategies based on the estimated pairwise tail dependencies improve performance relative to the benchmark index.

Natural Gradient Hybrid Variational Inference with Application to Deep Mixed Models

Stochastic models with global parameters $\bm{\theta}$ and latent variables $\bm{z}$ are common, and variational inference (VI) is popular for their estimation. This paper uses a variational approximation (VA) that comprises a Gaussian with factor covariance matrix for the marginal of $\bm{\theta}$, and the exact conditional posterior of $\bm{z}|\bm{\theta}$. Stochastic optimization for learning the VA only requires generation of $\bm{z}$ from its conditional posterior, while $\bm{\theta}$ is updated using the natural gradient, producing a hybrid VI method. We show that this is a well-defined natural gradient optimization algorithm for the joint posterior of $(\bm{z},\bm{\theta})$. Fast to compute expressions for the Tikhonov damped Fisher information matrix required to compute a stable natural gradient update are derived. We use the approach to estimate probabilistic Bayesian neural networks with random output layer coefficients to allow for heterogeneity. Simulations show that using the natural gradient is more efficient than using the ordinary gradient, and that the approach is faster and more accurate than two leading benchmark natural gradient VI methods. In a financial application we show that accounting for industry level heterogeneity using the deep model improves the accuracy of probabilistic prediction of asset pricing models.

Deep Distributional Time Series Models and the Probabilistic Forecasting of Intraday Electricity Prices

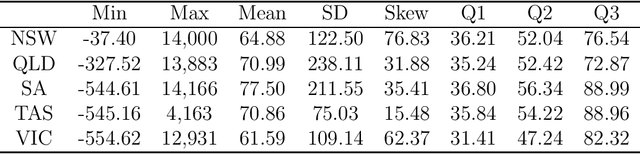
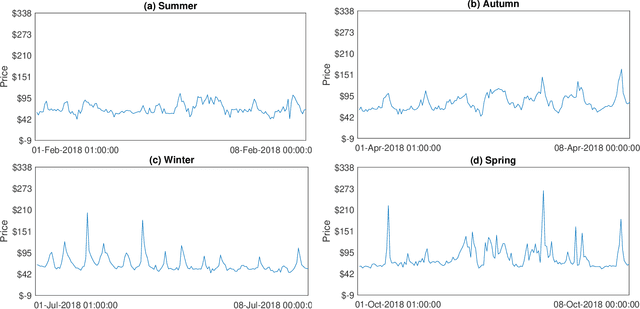
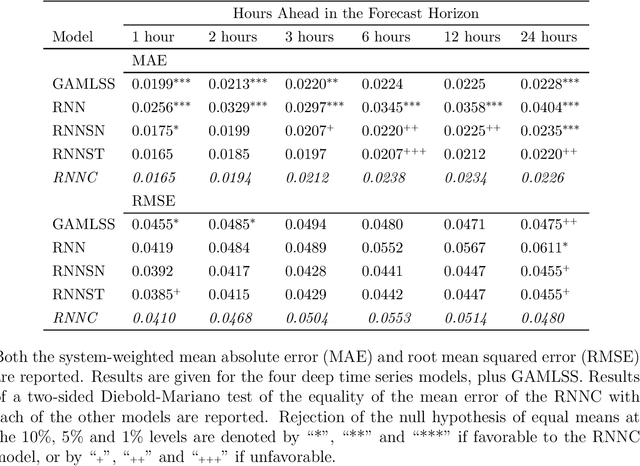
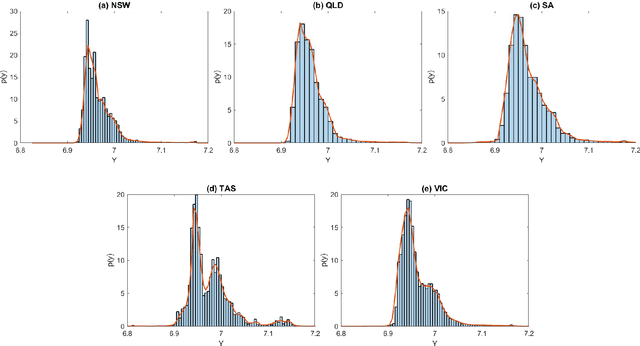
Recurrent neural networks (RNNs) with rich feature vectors of past values can provide accurate point forecasts for series that exhibit complex serial dependence. We propose two approaches to constructing deep time series probabilistic models based on a variant of RNN called an echo state network (ESN). The first is where the output layer of the ESN has stochastic disturbances and a shrinkage prior for additional regularization. The second approach employs the implicit copula of an ESN with Gaussian disturbances, which is a deep copula process on the feature space. Combining this copula with a non-parametrically estimated marginal distribution produces a deep distributional time series model. The resulting probabilistic forecasts are deep functions of the feature vector and also marginally calibrated. In both approaches, Bayesian Markov chain Monte Carlo methods are used to estimate the models and compute forecasts. The proposed deep time series models are suitable for the complex task of forecasting intraday electricity prices. Using data from the Australian National Electricity Market, we show that our models provide accurate probabilistic price forecasts. Moreover, the models provide a flexible framework for incorporating probabilistic forecasts of electricity demand as additional features. We demonstrate that doing so in the deep distributional time series model in particular, increases price forecast accuracy substantially.

Marginally-calibrated deep distributional regression

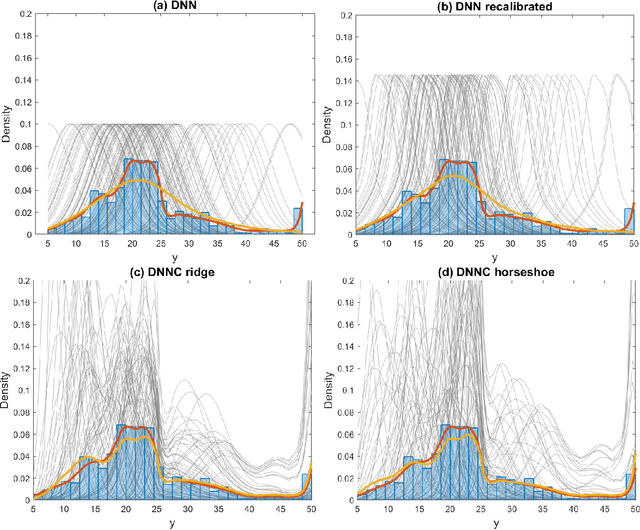
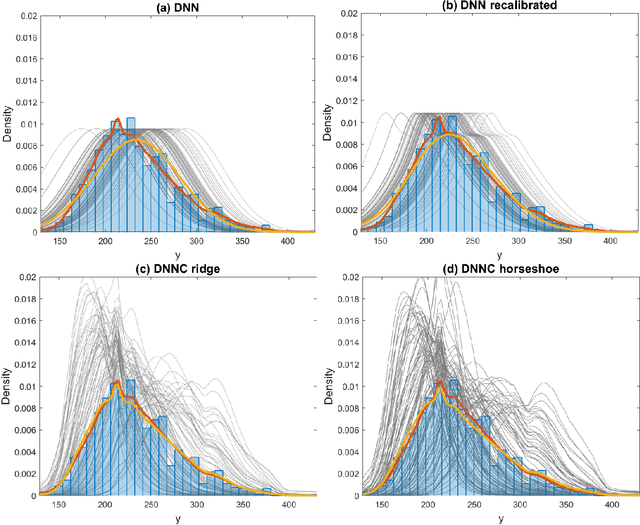
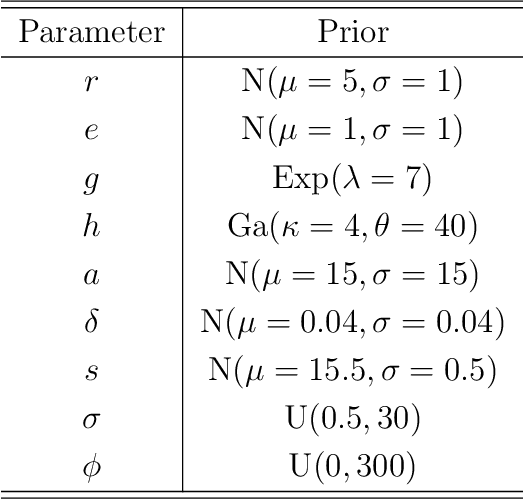
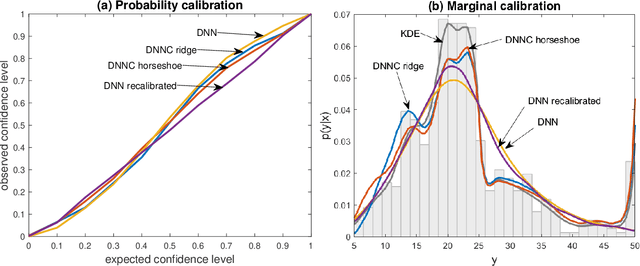
Deep neural network (DNN) regression models are widely used in applications requiring state-of-the-art predictive accuracy. However, until recently there has been little work on accurate uncertainty quantification for predictions from such models. We add to this literature by outlining an approach to constructing predictive distributions that are `marginally calibrated'. This is where the long run average of the predictive distributions of the response variable matches the observed empirical margin. Our approach considers a DNN regression with a conditionally Gaussian prior for the final layer weights, from which an implicit copula process on the feature space is extracted. This copula process is combined with a non-parametrically estimated marginal distribution for the response. The end result is a scalable distributional DNN regression method with marginally calibrated predictions, and our work complements existing methods for probability calibration. The approach is first illustrated using two applications of dense layer feed-forward neural networks. However, our main motivating applications are in likelihood-free inference, where distributional deep regression is used to estimate marginal posterior distributions. In two complex ecological time series examples we employ the implicit copulas of convolutional networks, and show that marginal calibration results in improved uncertainty quantification. Our approach also avoids the need for manual specification of summary statistics, a requirement that is burdensome for users and typical of competing likelihood-free inference methods.

Variational Bayes Estimation of Discrete-Margined Copula Models with Application to Time Series

We propose a new variational Bayes estimator for high-dimensional copulas with discrete, or a combination of discrete and continuous, margins. The method is based on a variational approximation to a tractable augmented posterior, and is faster than previous likelihood-based approaches. We use it to estimate drawable vine copulas for univariate and multivariate Markov ordinal and mixed time series. These have dimension $rT$, where $T$ is the number of observations and $r$ is the number of series, and are difficult to estimate using previous methods. The vine pair-copulas are carefully selected to allow for heteroskedasticity, which is a feature of most ordinal time series data. When combined with flexible margins, the resulting time series models also allow for other common features of ordinal data, such as zero inflation, multiple modes and under- or over-dispersion. Using six example series, we illustrate both the flexibility of the time series copula models, and the efficacy of the variational Bayes estimator for copulas of up to 792 dimensions and 60 parameters. This far exceeds the size and complexity of copula models for discrete data that can be estimated using previous methods.